The Universal Property of the Quotient

Let $H \triangleleft G$ . Then becomes a group under coset multiplication. Define the quotient map (or canonical projection) $\pi: G \rightarrow G/H$ by

$\pi(g) = gH.$

Proposition. If $H \triangleleft G$ , the quotient map $\pi: G \rightarrow G/H$ is a surjective homomorphism with kernel H.

Proof. If $a, b \in G$ , then

$\pi(a b) = (a b) H = a H \cdot b H = \pi(a) \pi(b).$

Therefore, $\pi$ is a group map.

Obviously, if $g H \in G/H$ , then $\pi(g) = g H$ . Hence, $\pi$ is surjective.

Finally, I'll show that $\ker \pi = H$ . If $h \in H$ , then $\pi(h) = h H = H$ , and H is the identity in . Therefore, $h \in \ker \pi$ , so $H \subset \ker \pi$ .

Conversely, suppose $g \in \ker \pi$ . Then $\pi(g) = H$ , so , so $g \in H$ . Therefore, $\ker \pi \subset H$ , and hence $H = \ker \pi$ .

The preceding lemma shows that every normal subgroup is the kernel of a homomorphism: If H is a normal subgroup of G, then $H = \ker \pi$ , where $\pi: G \to G/H$ is the quotient map. On the other hand, the kernel of a homomorphism is a normal subgroup.

Corollary. Normal subgroups are exactly the kernels of group homomorphisms.

Normality was defined with the idea of imposing a condition on subgroups which would make the set of cosets into a group. Now an apparently independent notion --- that of a homomorphism --- gives rise to the same idea! This strongly suggests that the definition of a normal subgroup was a good one.

You can think of quotient groups in an even more subtle way. The general theme is something like this. In modern mathematics, it is important to study not only objects --- like groups --- but the maps between objects --- in this case, group homomorphisms. The maps, after all, describe the relationships between different objects. (This theme is elaborated in a branch of mathematics called category theory.)

It turns out that more is true. In a sense, the maps carry all of the information about the objects; one could even be perverse and "build up" objects out of maps! I won't go to such extremes, but in some cases, an object can be characterized by certain maps. Here's an important example.

Theorem. ( Universal Property of the Quotient) Let $H \triangleleft G$ , and let $\phi: G \rightarrow K$ be a group homomorphism such that $H \subset \ker \phi$ . Then there is a unique homomorphism $\tilde\phi: G/H \rightarrow K$ such that the following diagram commutes:

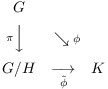
$\def\normalbaselines{\baselineskip20 pt \lineskip3 pt \lineskiplimit3 pt} \def\mapright#1{\smash{ \mathop{\longrightarrow}\limits_{#1}}} \def\mapdown#1{\llap{$\vcenter{\hbox{$\scriptstyle#1$}}$} \Big\downarrow} \def\mapse#1{\searrow \rlap{$\vcenter{\hbox{$\scriptstyle#1$}}$}} \matrix{ G & & \cr \mapdown{\pi} & \mapse{\phi} & \cr G/H & \mapright{\tilde\phi} & K \cr }$

(To say that the diagram commutes means that $\tilde{\phi} \cdot \pi = \phi$ .)

Proof. Define $\tilde\phi: G/H \rightarrow K$ by

$\tilde\phi(gH) = \phi(g).$

This is forced by the requirement that $\tilde\phi\pi = \phi$ , since plugging $g \in G$ into both sides yields $\tilde\phi\pi(g) = \phi(g)$ , or $\tilde\phi(gH) = \phi(g)$ .

I need to check that this map is well-defined. The point is that a given coset may in general be written as , where $g \ne g'$ . I must verify that the result $\phi(g)$ or $\phi(g')$ is the same regardless of how I write the coset.

(If $\phi(g) \ne \phi(g')$ in this situation, then a single input --- the coset --- produces different outputs, which contradicts what it means to be a function.)

So suppose that , so for some $h \in H$ .

$\tilde{\phi}(g H) = \phi(g) = \phi(g' h) = \phi(g') \phi(h) = \phi(g') \cdot 1 = \phi(g') = \tilde{\phi}(g' H).$

This shows that $\tilde\phi$ is indeed well-defined.

I was forced to define $\tilde\phi$ as I did in order to make the diagram commute. Hence, $\tilde\phi$ is unique.

Now I'll show that $\tilde\phi$ is a homomorphism. Let $a, b \in G$ . Then

$\tilde{\phi}\left((a H) (b H)\right) = \tilde{\phi}\left((a b) H\right) = \phi(a b) = \phi(a) \phi(b) = \tilde{\phi}(a H) \tilde{\phi}(b H).$

Therefore, $\tilde\phi$ is a homomorphism.

The universal property of the quotient is an important tool in constructing group maps: To define a map out of a quotient group , define a map out of G which maps H to 1.

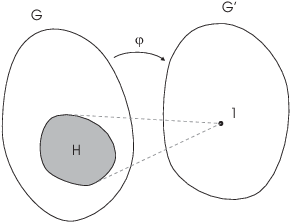
$\hbox{\epsfysize=2 in \epsffile{universal-property-of-the-quotient-1.eps}}$

The map you construct goes from G to ; the universal property automatically constructs a map $G/H \to G'$ for you. The advantage of using the universal property rather than defining a map out of directly is that you don't repeat the verification that the map is well-defined --- it's been done once and for all in the proof above.

Should you ever need to know how the magic map $\tilde\phi$ is defined, refer to the proof (and the commutativity of the diagram).

Remarks. (a) Many other constructions are characterized by universal properties. In each case, one finds that the appropriate conditions imply the existence of a unique map with certain properties.

(a) The use of diagrams of maps --- particularly commutative ones --- is pervasive in modern mathematics. They are a powerful language, and another outgrowth of the categorical point of view. In general, one says a diagram commutes if following the "paths" indicated by the arrows (maps) in different ways between two objects produces the same result. For example, consider the diagram

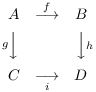
$\def\normalbaselines{\baselineskip20 pt \lineskip3 pt \lineskiplimit3 pt} \def\maprightbottom#1{\smash{ \mathop{\longrightarrow}\limits_{#1}}} \def\maprighttop#1{\smash{ \mathop{\longrightarrow}\limits^{#1}}} \def\mapdownleft#1{\llap{$\vcenter{\hbox{$\scriptstyle#1$}}$} \Big\downarrow} \def\mapdownright#1{\Big\downarrow \rlap{$\vcenter{\hbox{$\scriptstyle#1$}}$}} \matrix{ A & \maprighttop{f} & B \cr \mapdownleft{g} & & \mapdownright{h} \cr C & \maprightbottom{i} & D \cr }$

To say that this diagram commutes means that $h \cdot f = i \cdot g$ .

Example. Use the universal property to show that $f: \integer_8 \to \integer_{12}$ given by is a well-defined group map.

I can regard $\integer_8$ as $\dfrac{\integer}{8 \integer}$ . To define f, begin by defining $f': \integer \to \integer_{12}$ by

Let $8 n \in 8 \integer$ . Then since 24 is a multiple of 12,

$f'(8 n) = 3 \cdot 8 n = 24 n = 0.$

This means that maps the subgroup $8 \integer$ of $\integer$ to the identity $0 \in \integer_{12}$ . By the universal property of the quotient, induces a map $f: \dfrac{\integer}{8 \integer} \to \integer_{12}$ given by

$f(x + 8 \integer) = 3 x.$

I can identify $x + 8 \integer$ with $x \mod{8} \in \integer_8$ by reducing mod 8 if needed. (Thus, $11 + 8 \integer \in \dfrac{\integer}{8 \integer}$ is identified with $3 \in \integer_8$ .) Then the definition of f becomes

This is the group map I wanted to construct.

Example. ( Using the universal property to construct a group map) Use the universal property to construct a homomorphism from the quotient group $\dfrac{\integer \times \integer}{\langle (5, 2)\rangle}$ to $\integer$ .

The universal property tells me to construct a group map from $\integer \times \integer$ to $\integer$ which contains $\langle (5, 2)\rangle$ in its kernel --- that is, which sends $\langle (5, 2)\rangle$ to 0. Now $\langle (5, 2)\rangle$ consists of all multiples of , so what I'm looking for is a group map which sends to 0.

To ensure that what I get is a group map, I should probably guess a linear function --- something like

If , then . There is no question of solving this equation for a and b, since there is one equation and two variables. But I just need some a and b that work --- and one "obvious" way to do this is to set and , since

Notice that , would work, too. In fact, there are infinitely many possibilities.

So I define $f: \integer \times \integer \to \integer$ by

It's easy to check that this is a group map, and I constructed it so that $\langle (5, 2)\rangle \subset \ker f$ . Therefore, the universal property automatically produces a group map $\tilde{f}: \dfrac{\integer \times \integer}{\langle (5, 2)\rangle} \to \integer$ . It is defined by

$\tilde{f}\left((x, y) + \langle (5, 2)\rangle\right) = 2 x - 5 y.$

Why not just define the map this way to begin with? If you did, you'd have to check that the map was well-defined. It's less messy to use the universal property to construct the map as above.

Contact information

Bruce Ikenaga's Home Page