The Cayley-Hamilton Theorem

Terminology. A linear transformation T from a vector space V to itself (i.e. $T: V \to V$ ) is called a linear operator on V.

Theorem. (Cayley-Hamilton) Let $T: V \rightarrow V$ be a linear operator on a finite dimensional vector space V. Let p be the characteristic polynomial of T. Then $p(T) = 0$ .

Proof. Choose a basis ${\cal B} = \{v_1, \ldots, v_n\}$ for V. I will show that $p(T) = 0$ by showing that $p(T)v_i = 0$ for all i.

Let $A = [T]_{{\cal B}, {\cal B}}$ . Then

$$Tv_i = \sum_j A_{ji}v_j, \qquad i = 1, \ldots, n.$$

Now

$$Tv_i = \sum_j \delta{ij} Tv_j, \quad\hbox{so}\quad \sum_j \left(A_{ji} I - \delta{ij} T\right)v_j = 0.$$

To save writing, let

$$B_{ij} = A_{ji} I - \delta{ij} T.$$

Observe that the matrix $B = (B_{ij})$ has linear operators as its entries. For example, for $n = 2$ ,

$$\left[\matrix{A_{11} I - T & A_{21} I \cr A_{12} I & A_{22} I - T \cr}\right].$$

In fact, B is just the transpose of $A - \lambda I$ with $\lambda = T$ . Hence, $|B| = p(T)$ .

Next, I will show that $|B|v_k = 0$ for all k. Observe that

$$\sum_j B_{ij} v_j = 0.$$

Hence,

$$0 = (\adj B)_{ki} \sum_j B_{ij} v_j = \sum_j (\adj B)_{ki} B_{ij} v_j.$$

This equation holds for all i and all k, so I'll still get 0 if I sum on i. So I'll sum on i, then interchange the order of summation:

$$0 = \sum_i \sum_j (\adj B)_{ki} B_{ij} v_j,$$

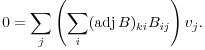
$$0 = \sum_j \left(\sum_i (\adj B)_{ki} B_{ij}\right) v_j.$$

Now $\sum_i (\adj B)_{ki} B_{ij}$ is the $(k, j)$ -th entry of $(\adj B\cdot B) = |B| I$ . Hence,

$$0 = \sum_j |B| \delta{kj} v_j = |B| v_k.$$

Since $p(T) = |B|$ kills $v_k$ for all k, $p(T) = 0$ .

Definition. If A is an $n \times n$ matrix, the minimal polynomial of A is the polynomial $m(x)$ of smallest degree with leading coefficient 1 such that $m(A) = 0$ . If T is a linear operator on a vector space V, the minimal polynomial of T is the minimal polynomial of any matrix for T.

It's implicit in the last sentence that it doesn't matter which matrix for T you use. Can you prove it?

Corollary. The minimal polynomial divides the characteristic polynomial.

Example. Consider the matrix

$$A = \left[\matrix{9 & 1 & 3 \cr -3 & 1 & -1 \cr -16 & -2 & -5 \cr}\right] \in M(3, \real).$$

The characteristic polynomial is $4 - 8 \lambda + 5 \lambda^2 - \lambda^3$ ; the eigenvalues are $\lambda = 2$ (double) and $\lambda = 1$ .

Since A is evidently neither 0 nor a multiple of the identity, its minimal polynomial must be a quadratic or cubic factor of the characteristic polynomial.

Note that

$$(A - 2I)(A - I) = \left[\matrix{5 & 1 & 2 \cr -5 & -1 & -2 \cr -10 & -2 & -4 \cr}\right] \quad\hbox{and}\quad (A - 2I)^2 = \left[\matrix{-2 & 0 & -1 \cr -2 & 0 & -1 \cr 6 & 0 & 3 \cr}\right].$$

Hence, the minimal polynomial is the characteristic polynomial $4 - 8 \lambda + 5 \lambda^2 - \lambda^3$ .

Here is a more precise version of the previous corollary.

Proposition. Let $T: V \rightarrow V$ be a linear operator on a finite dimensional vector space. The minimal and characteristic polynomials of T have the same roots, up to multiplicity.

Proof. Let $m(x)$ denote the minimal polynomial and $p(x)$ the characteristic polynomial. Cayley-Hamilton says that $m \mid p$ , so a root of m is a root of p.

Conversely, let $\lambda$ be a root of p --- i.e. an eigenvalue. Let v be an eigenvector corresponding to $\lambda$ , so $Tv = \lambda v$ . It follows that if $f(x)$ is an arbitrary polynomial over F, then $f(T)v = f(\lambda)v$ . In particular, this is true of the minimal polynomial:

$$0 = m(T)v = m(\lambda)v.$$

Since $v \ne 0$ , $m(\lambda) = 0$ . Therefore, every root of p is a root of m, and the roots of m and p coincide.

Example. Consider the matrix

$$A = \left[\matrix{9 & 1 & 3 \cr -3 & 1 & -1 \cr -16 & -2 & -5 \cr}\right] \in M(3, \real).$$

The characteristic polynomial is $4 - 8 \lambda + 5 \lambda^2 - \lambda^3 = (\lambda - 2)^2(\lambda - 1)$ . In view of the Corollary, I did more work than necessary in determining the minimal polynomial the first time. The only possibilities for the minimal polynomial are $(\lambda - 2)^2(\lambda - 1)$ and $(\lambda - 2)(\lambda - 1)$ .

Computation showed that $(\lambda - 2)(\lambda - 1)$ doesn't kill A, so the minimal polynomial is $(\lambda - 2)^2(\lambda - 1)$ .

Send comments about this page to: Bruce.Ikenaga@millersville.edu.

Bruce Ikenaga's Home Page

Copyright 2011 by Bruce Ikenaga