Eigenvalues and Eigenvectors

Definition. Let $A \in M_n(F)$ . The characteristic polynomial of A is

$$p(\lambda) = \det (A - \lambda I).$$

(I is the $n \times n$ identity matrix.)

A root of the characteristic polynomial is called an eigenvalue (or a characteristic value) of A.

While the entries of A come from the field F, it makes sense to ask for the roots of $p(\lambda)$ in an extension field E of F. For example, if A is a matrix with real entries, you can ask for the eigenvalues of A in $\real$ or in $\complex$ .

Example. Consider the matrix

$$A = \left[\matrix{0 & 1 \cr -1 & 0 \cr}\right].$$

The characteristic polynomial is $x^2 + 1$ . Hence, A has no eigenvalues in $\real$ . Its eigenvalues in $\complex$ are $\lambda = \pm i$ .

Example. Let

$$A = \left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \in M(3, \real).$$

You can use row and column operations to simplify the computation of $\det(A - \lambda I)$ :

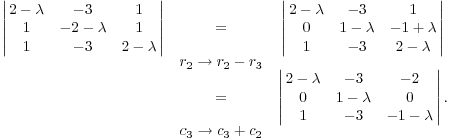
$$\matrix{ \left|\matrix{2 - \lambda & -3 & 1 \cr 1 & -2 - \lambda & 1 \cr 1 & -3 & 2 - \lambda \cr}\right| & = & \left|\matrix{2 - \lambda & -3 & 1 \cr 0 & 1 - \lambda & -1 + \lambda \cr 1 & -3 & 2 - \lambda \cr}\right| \cr & r_2 \to r_2 - r_3 & \cr & = & \left|\matrix{2 - \lambda & -3 & -2 \cr 0 & 1 - \lambda & 0 \cr 1 & -3 & -1 - \lambda \cr}\right|.\cr & c_3 \to c_3 + c_2 & \cr}$$

(Adding a multiple of a row or a column to a row or column, respectively, does not change the determinant.) Now expand by cofactors of the second row:

$$(1 - \lambda)\left((2 - \lambda)(-1 - \lambda) + 2\right) = (1 - \lambda)(\lambda^2 - \lambda) = -\lambda(\lambda - 1)^2.$$

The eigenvalues are $\lambda = 0$ , $\lambda = 1$ (double).

Example. A matrix $A \in M_n(F)$ is upper triangular if $A_{ij} = 0$ for $i > j$ . Thus, the entries below the main diagonal are zero. ( Lower triangular matrices are defined in an analogous way.)

The eigenvalues of a triangular matrix

$$A = \left[\matrix{\lambda_1 & * & \cdots & * \cr 0 & \lambda_2 & \cdots & * \cr \vdots & \vdots & \ddots & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right]$$

are just the diagonal entries $\lambda_1, \ldots, \lambda_n$ . (You can prove this by induction on n.)

Remark. To find the eigenvalues of a matrix, you need to find the roots of the characteristic polynomial.

There are formulas for finding the roots of polynomials of degree $\le 4$ . (For example, the quadratic formula gives the roots of a quadratic equation $ax^2 + bx + c = 0$ .) However, Abel showed in the early part of the 19-th century that the general quintic is not solvable by radicals. (For example, $2x^5 - 5x^4 + 5$ is not solvable by radicals over $\rational$ .) In the real world, the computation of eigenvalues often requires numerical approximation.

If $\lambda$ is an eigenvalue of A, then $\det(A - \lambda I) = 0$ . Hence, the $n \times n$ matrix $A - \lambda I$ is not invertible. It follows that $A - \lambda I$ must row reduce to a row reduced echelon matrix R with fewer than n leading coefficients. Thus, the system $Rx = 0$ has at least one free variable, and hence has more than one solution. In particular, $Rx = 0$ --- and therefore, $(A - \lambda I)x = 0$ --- has at least one nonzero solution.

Definition. Let $A \in M_n(F)$ , and let $\lambda$ be an eigenvalue of A. An eigenvector (or a characteristic vector) of A for $\lambda$ is a nonzero vector $v \in F^n$ such that

$$Av = \lambda v.$$

Equivalently,

$$(A - \lambda I)v = 0.$$

Example. Let

$$A = \left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \in M(3, \real).$$

The eigenvalues are $\lambda = 0$ , $\lambda = 1$ (double).

First, I'll find an eigenvector for $\lambda = 0$ .

$$A - 0\cdot I = \left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right].$$

I want $v = (a, b, c)$ such that

$$\left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

You can solve the system by row reduction. Since the column of zeros on the right will never change, it's enough to row reduce the $3 \times 3$ matrix on the right.

$$\left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \quad \to \quad \left[\matrix{1 & 0 & -1 \cr 0 & 1 & -1 \cr 0 & 0 & 0 \cr}\right]$$

This says

$$\matrix{a & & & - & c & = & 0 \cr & & b & - & c & = & 0 \cr}$$

Therefore, $a = c$ , $b = c$ , and the eigenvector is

$$\left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{c \cr c \cr c \cr}\right] = c \left[\matrix{1 \cr 1 \cr 1 \cr}\right].$$

Notice that this is the usual algorithm for finding a basis for the solution space of a homogeneous system (or the null space of a matrix).

I can set c to any nonzero number. For example, $c = 1$ gives the eigenvector $(1, 1, 1)$ . Notice that there are infinitely many eigenvectors for this eigenvalue, but all of these eigenvectors are multiples of $(1,1,1)$ .

Likewise,

$$A - I = \left[\matrix{1 & -3 & 1 \cr 1 & -3 & 1 \cr 1 & -3 & 1 \cr}\right] \quad \to \quad \left[\matrix{1 & -3 & 1 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}\right]$$

Hence, the eigenvectors are

$$\left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{3b - c \cr b \cr c \cr}\right] = b \left[\matrix{3 \cr 1 \cr 0 \cr}\right] + c \left[\matrix{-1 \cr 0 \cr 1 \cr}\right].$$

Taking $b = 1$ , $c = 0$ gives $(3, 1, 0)$ ; taking $b = 0$ , $c = 1$ gives $(-1, 0, 1)$ . This eigenvalue gives rise to two independent eigenvectors.

Note, however, that a double root of the characteristic polynomial need not give rise to two independent eigenvectors.

Definition. Matrices $A, B \in M(n, F)$ are similar if there is an invertible matrix $P \in M(n, F)$ such that $PAP^{-1} = B$ .

Lemma. Similar matrices have the same characteristic polynomial (and hence the same eigenvalues).

Proof.

$$PAP^{-1} - \lambda I = PAP^{-1} - \lambda PIP^{-1} = P(A - \lambda I)P^{-1}.$$

Therefore, the matrices $A - \lambda I$ and $PAP^{-1} - \lambda I$ are similar. Hence, they have the same determinant. The determinant of $A - \lambda I$ is the characteristic polynomial of A and the determinant of $PAP^{-1} - \lambda I$ is the characteristic polynomial of $PAP^{-1}$ .

Definition. Let $T: V \rightarrow V$ be a linear transformation, where V is a finite-dimensional vector space. The characteristic polynomial of T is the characteristic polynomial of a matrix of T relative to a basis ${\cal B}$ of V.

The preceding lemma shows that this is independent of the choice of basis. For if ${\cal B}$ and ${\cal C}$ are bases for V, then

$$[T]_{{\cal C},{\cal C}} = [{\cal B} \to {\cal C}][T]_{{\cal B},{\cal B}} [{\cal C} \to {\cal B}] = [{\cal B} \to {\cal C}][T]_{{\cal B},{\cal B}} [{\cal B} \to {\cal C}]^{-1}.$$

Therefore, $[T]_{{\cal C},{\cal C}}$ and $[T]_{{\cal B},{\cal B}}$ are similar, so they have the same characteristic polynomial.

This shows that it makes sense to speak of the eigenvalues and eigenvectors of a linear transformation T.

Definition. A matrix $A \in M_n(F)$ is diagonalizable if A has n independent eigenvectors --- that is, if there is a basis for $F^n$ consisting of eigenvectors of A.

Proposition. $A \in M_n(F)$ is diagonalizable if and only if it is similar to a diagonal matrix.

Proof. Let $\{v_1, \ldots, v_n\}$ be n independent eigenvectors for A corresponding to eigenvalues $\{\lambda_1, \ldots, \lambda_n\}$ . Let T be the linear transformation corresponding to A:

$$T(v) = Av.$$

Since $Av_i = \lambda_i v_i$ for all i, the matrix of T relative to the basis ${\cal B} = \{v_1, \ldots, v_n\}$ is

$$[T]_{{\cal B}, {\cal B}} = \left[\matrix{\lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right].$$

Now A is the matrix of T relative to the standard basis, so

$$[T]_{{\cal B}, {\cal B}} = [{\rm std} \to {\cal B}]\cdot A\cdot [{\cal B} \to {\rm std}].$$

The matrix $[{\cal B} \to {\rm std}]$ is obtained by building a matrix using the $v_1, \ldots, v_n$ as the columns. Then $[{\rm std} \to {\cal B}] = [{\cal B} \to {\rm std}]^{-1}$ .

Hence,

$$\left[\matrix{\lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right] = [{\cal B} \to {\rm std}]^{-1}\cdot A \cdot [{\cal B} \to {\rm std}].$$

Conversely, if D is diagonal, P is invertible, and $D = P^{-1}AP$ , the columns $c_1, \ldots, c_n$ of P are independent eigenvectors for A. In fact, if

$$D = \left[\matrix{\lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right],$$

then $PD = AP$ says

$$\left[\matrix{\uparrow & \uparrow & & \uparrow \cr c_1 & c_2 & \cdots & c_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{\lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right] = A \left[\matrix{\uparrow & \uparrow & & \uparrow \cr c_1 & c_2 & \cdots & c_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

Hence, $\lambda_i c_i = Ac_i$ .

Example. Consider the matrix matrix

$$A = \left[\matrix{2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \in M(3, \real).$$

In an earlier example, I showed that A has 3 independent eigenvectors $(1, 1, 1)$ , $(3, 1, 0)$ , $(-1, 0, 1)$ . Therefore, A is diagonalizable.

To find a diagonalizing matrix, build a matrix using the eigenvectors as the columns:

$$P = \left[\matrix{ 1 & 3 & 1 \cr 1 & 1 & 0 \cr 1 & 0 & 1 \cr}\right].$$

You can check by finding $P^{-1}$ and doing the multiplication that you get a diagonal matrix:

$$P^{-1} A P = \left[\matrix{ 1 & 3 & 1 \cr 1 & 1 & 0 \cr 1 & 0 & 1 \cr}\right]^{-1} \left[\matrix{ 2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \left[\matrix{ 1 & 3 & 1 \cr 1 & 1 & 0 \cr 1 & 0 & 1 \cr}\right] =$$

$$\left[\matrix{ -1 & 3 & -1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \left[\matrix{ 2 & -3 & 1 \cr 1 & -2 & 1 \cr 1 & -3 & 2 \cr}\right] \left[\matrix{ 1 & 3 & 1 \cr 1 & 1 & 0 \cr 1 & 0 & 1 \cr}\right] = \left[\matrix{ 0 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right].$$

Of course, I knew this was the answer! I should get a diagonal matrix with the eigenvalues on the main diagonal, in the same order that I put the corresponding eigenvectors into P.

You can put the eigenvectors in as the columns of P in any order: A different order will give a diagonal matrix with the eigenvalues on the main diagonal in a different order.

Example. Let

$$A = \left[\matrix{ 4 & -4 & -5 \cr 1 & 0 & -3 \cr 0 & 0 & 2 \cr}\right] \in M(3, \real).$$

Find the eigenvalues and, for each eigenvalue, a complete set of eigenvectors. If A is diagonalizable, find a matrix P such that $P^{-1}AP$ is a diagonal matrix.

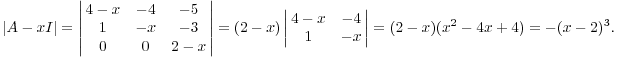
$$|A - xI| = \left|\matrix{ 4 - x & -4 & -5 \cr 1 & -x & -3 \cr 0 & 0 & 2 - x \cr}\right| = (2 - x)\left|\matrix{ 4 - x & -4 \cr 1 & -x \cr}\right| = (2 - x)(x^2 - 4x + 4) = -(x - 2)^3.$$

The eigenvalue is $x = 2$ .

Now

$$A - 2I = \left[\matrix{ 2 & -4 & -5 \cr 1 & -2 & -3 \cr 0 & 0 & 0 \cr}\right] \to \left[\matrix{ 1 & -2 & 0 \cr 0 & 0 & 1 \cr 0 & 0 & 0 \cr}\right].$$

Thinking of this as the coefficient matrix of a homogeneous linear system with variables a, b, and c, I obtain the equations

$$a - 2 b = 0, \quad c = 0.$$

Then $a = 2 b$ , so

$$\left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{2b \cr b \cr 0 \cr}\right] = b\cdot \left[\matrix{2 \cr 1 \cr 0 \cr}\right].$$

$(2, 1, 0)$ is an eigenvector. Since there's only one independent eigenvector --- as opposed to 3 --- the matrix A is not diagonalizable.

Example. The following matrixhas eigenvalue $\lambda = 1$ (a triple root):

$$B = \left[\matrix{-3 & 3 & -5 \cr 12 & -7 & 14 \cr 10 & -7 & 13 \cr}\right] \in M(3, \real).$$

Now

$$B - 1\cdot I = \left[\matrix{ -4 & 3 & -5 \cr 12 & -8 & 14 \cr 10 & -7 & 12 \cr}\right] \to \left[\matrix{ 1 & 0 & \dfrac{1}{2} \cr 0 & 1 & -1 \cr 0 & 0 & 0 \cr}\right]$$

Thinking of this as the coefficient matrix of a homogeneous linear system with variables a, b, and c, I obtain the equations

$$a + \dfrac{1}{2}c = 0, \quad b - c = 0.$$

Set $c = 2$ . This gives $a = -1$ and $b = 2$ . Thus, the only eigenvectors are the nonzero multiples of $(-1, 2, 2)$ . Since there is only one independent eigenvectors, B is not diagonalizable.

Proposition. Let $T: V \rightarrow V$ be a linear transformation on an n dimensional vector space. If $v_1, \ldots, v_n$ are eigenvectors corresponding to the distinct eigenvalues $\lambda_1, \ldots, \lambda_n$ , then $\{v_1, \ldots, v_n\}$ is independent.

Proof. Suppose to the contrary that $\{v_1, \ldots, v_n\}$ is dependent. Let p be the smallest number such that the subset $\{v_1, \ldots, v_p\}$ is dependent. Then there is a nontrivial linear relation

$$a_1 v_1 + \cdots a_p v_p = 0.$$

Note that $a_p \ne 0$ , else

$$a_1 v_1 + \cdots a_{p-1} v_{p-1} = 0.$$

This would contradict minimality of p.

Hence, I can rewrite the equation above in the form

$$v_p = b_1 v_1 + \cdots + b_{p-1} v_{p-1}.$$

Apply T to both sides, and use $Tv_i = \lambda_i v_i$ :

$$\lambda_p v_p = b_1 \lambda_1 v_1 + \cdots + b_{p-1} \lambda_{p-1} v_{p-1}.$$

On the other hand,

$$\lambda_p v_p = \lambda_p b_1 v_1 + \cdots + \lambda_p b_{p-1} v_{p-1}.$$

Subtract the last equation from the one before it to obtain

$$0 = b_1(\lambda_1 - \lambda_p)v_1 + \cdots + b_{p-1}(\lambda_{p-1} - \lambda_p)v_{p-1}.$$

Since the eigenvalues are distinct, the terms $\lambda_p - \lambda_i$ are nonzero. Hence, this is a linear relation in $v_1, \ldots, v_{p-1}$ which contradicts minimality of p --- unless $b_1 = \cdots = b_{p-1} = 0$ .

In this case, $v_p = 0$ , which contradicts the fact that $v_p$ is an eigenvector. Therefore, the original set must in fact be independent.

Example. Let A be an $n \times n$ real matrix. The complex eigenvalues of A always come in conjugate pairs $a + bi$ and $a - bi$ .

Moreover, if v is an eigenvector for $\lambda = a + bi$ , then the conjugate $v^*$ is an eigenvector for $\lambda^* = a - bi$ .

For suppose $Av = \lambda v$ . Taking complex conjugates, I get

$$A^* v^* = \lambda^* v^*, \quad Av^* = \lambda^* v^*.$$

($A^* = A$ because A is a real matrix.)

In practical terms, this means that once you've found an eigenvector for one complex eigenvalue, you can get an eigenvector for the conjugate eigenvalue by taking the conjugate of the eigenvector. You don't need to do a separate eigenvector computation.

For example, suppose

$$A = \left[\matrix{1 & -1 \cr 2 & 3 \cr}\right] \in M(2, \real).$$

The characteristic polynomial is $\lambda^2 - 4\lambda + 5$ . The eigenvalues are $2 \pm i$ .

Find an eigenvector for $\lambda = 2 + i$ :

$$A - (2 + i)I = \left[\matrix{-1 - i & -1 \cr 2 & 2 - i \cr}\right] \to \left[\matrix{-1 - i & -1 \cr 0 & 0 \cr}\right]$$

I knew that the second row $(2, 2 - i)$ must be a multiple of the first row, because I know the system has nontrivial solutions. So I don't have to work out what multiple it is; I can just zero out the second row on general principles.

This only works for $2 \times 2$ matrices, and only for those which are $A - \lambda I$ 's in eigenvector computations.

Next, there's no point in going all the way to row reduced echelon form. I just need some nonzero vector $(a,b)$ such that

$$\left[\matrix{-1 - i & -1 \cr 0 & 0 \cr}\right] \left[\matrix{a \cr b \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right].$$

That is, I want

$$(-1 - i)a + (-1)b = 0.$$

I can find an a and b that work by swapping $-1 - i$ and -1, and negating one of them. For example, take $a = 1$ (-1 negated) and $b = -1 - i$ . This checks:

$$(-1 - i)(1) + (-1)(-1 - i) = 0.$$

So $(a,b) = (1, -1 - i)$ is an eigenvector for $\lambda = 2 + i$ .

By the discussion at the start of the example, I don't need to do a computation for $\lambda = 2 - i$ . Just conjugate the previous eigenvector: $(1, -1 + i)$ must be an eigenvector for $2 - i$ .

Since there are 2 independent eigenvectors, you can use them construct a diagonalizing matrix for A:

$$\left[\matrix{1 & 1 \cr -1 - i & -1 + i \cr}\right]^{-1} \left[\matrix{1 & -1 \cr 2 & 3 \cr}\right] \left[\matrix{1 & 1 \cr -1 - i & -1 + i \cr}\right] = \left[\matrix{2 + i & 0 \cr 0 & 2 - i \cr}\right].$$

Notice that you get a diagonal matrix with the eigenvalues on the main diagonal, in the same order in which you listed the eigenvectors.

Example. For the following matrix, find the eigenvalues over $\complex$ , and for each eigenvalue, a complete set of independent eigenvectors.

Find a diagonalizing matrix and the corresponding diagonal matrix.

$$A = \left[\matrix{ -2 & 0 & 5 \cr 0 & 2 & 0 \cr -5 & 0 & 4 \cr}\right].$$

The characteristic polynomial is

$$|A - x I| = \left|\matrix{ -2 - x & 0 & 5 \cr 0 & 2 - x & 0 \cr -5 & 0 & 4 - x \cr}\right| = (2 - x) \left|\matrix{ -2 - x & 5 \cr -5 & 4 - x \cr}\right| = (2 - x)[(x + 2)(x - 4) + 25] =$$

$$(2 - x)(x^2 - 2 x + 17).$$

Now

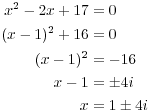
$$\eqalign{ x^2 - 2 x + 17 & = 0 \cr (x - 1)^2 + 16 & = 0 \cr (x - 1)^2 & = -16 \cr x - 1 & = \pm 4 i \cr x & = 1 \pm 4 i \cr}$$

The eigenvalues are $x = 2$ and $x = 1 \pm 4 i$ .

For $x = 2$ , I have

$$A - 2 I = \left[\matrix{ -4 & 0 & 5 \cr 0 & 0 & 0 \cr -5 & 0 & 2 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 0 & 1 \cr 0 & 0 & 0 \cr}\right].$$

With variables a, b, and c, the corresponding homogeneous system is $a = 0$ and $c = 0$ . This gives the solution vector

$$\left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr b \cr 0 \cr}\right] = b \cdot \left[\matrix{0 \cr 1 \cr 0 \cr}\right].$$

Taking $b = 1$ , I obtain the eigenvector $(0, 1, 0)$ .

For $x = 1 + 4 i$ , I have

$$\left[\matrix{ -3 - 4 i & 0 & 5 \cr 0 & 1 - 4 i & 0 \cr -5 & 0 & 3 - 4 i \cr}\right] \quad \to \quad \left[\matrix{ -5 & 0 & 3 - 4 i \cr 0 & 1 & 0 \cr -5 & 0 & 3 - 4 i \cr}\right]$$

I multiplied the first row by $3 - 4 i$ , then divided it by 5. This made it the same as the third row.

I divided the second row by $1 - 4 i$ .

(I knew the the first and third rows had to be multiples, since they're clearly independent of the second row. Thus, if they weren't multiples, the three rows would be independent, the eigenvector matrix would be invertible, and there would be no eigenvectors [which must be nonzero].)

Now I can wipe out the third row by subtracting the first:

$$\left[\matrix{ -5 & 0 & 3 - 4 i \cr 0 & 1 & 0 \cr -5 & 0 & 3 - 4 i \cr}\right] \quad \to \quad \left[\matrix{ -5 & 0 & 3 - 4 i \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}\right].$$

With variables a, b, and c, the corresponding homogeneous system is

$$-5 a + (3 - 4 i)c = 0 \quad\hbox{and}\quad b = 0.$$

There will only be one parameter (c), so there will only be one independent eigenvector. To get one, switch the "-5" and "$3 - 4i$ " and negate the "-5" to get "5". This gives $a = 3 - 4 i$ , $b = 0$ , and $c = 5$ . You can see that these values for a and c work:

$$(-5)(3 - 4 i) + (3 - 4i)(5) = 0.$$

Thus, my eigenvector is $(3 - 4 i, 0, 5)$ .

Hence, an eigenvector for $1 - 4 i$ is the conjugate $(3 + 4 i, 0, 5)$ .

A diagonalizing matrix is given by

$$P = \left[\matrix{ 0 & 3 - 4 i & 3 + 4 i \cr 1 & 0 & 0 \cr 0 & 5 & 5 \cr}\right].$$

With this diagonalizing matrix, I have

$$P^{-1} A P = \left[\matrix{ 2 & 0 & 0 \cr 0 & 1 + 4 i & 0 \cr 0 & 0 & 1 - 4 i \cr}\right].\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2011 by Bruce Ikenaga