Matrix Arithmetic

Most of linear algebra involves mathematical objects called matrices. A matrix is a finite rectangular array of numbers:

$$\left[\matrix{ 1 & -3 & 0 & 5 \cr 3 & 0 & -17 & 9 \cr -1 & -2 & 4 & -3 \cr}\right] \quad \left[\matrix{0 \cr 5 \cr -5 \cr 3 \cr -3.14 \cr}\right] \quad \left[\matrix{\dfrac{17}{5} & -4 & 0 & \dfrac{1}{2} \cr}\right] \quad \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right]$$

In this case, the numbers are elements of $\rational$ (or $\real$ ). In general, the entries will be elements of some commutative ring or field.

In this section, I'll explain operations with matrices by example. I'll discuss and prove some of the properties of these operations later on.

Dimensions of matrices. An $m \times n$ matrix is a matrix with m rows and n columns. Sometimes this is expressed by saying that the dimensions of the matrix are $m \times n$ .

$$\matrix{\left[\matrix{1 & 2 & 3 \cr 4 & 5 & 6 \cr}\right] & \left[\matrix{0 & 0 \cr 0 & 0 \cr 0 & 0 \cr 0 & 0 \cr}\right] & \left[\matrix{\pi \cr}\right] \cr \quad\hbox{a}\quad 2 \times 3 \quad\hbox{matrix}\quad & \quad\hbox{a}\quad 4 \times 2 \quad\hbox{matrix}\quad & \quad\hbox{a}\quad 1 \times 1 \quad\hbox{matrix}\quad \cr}$$

A $1 \times n$ matrix is called an n-dimensional row vector. For example, here's a 3-dimensional row vector:

$$\left[\matrix{4 & \sqrt{17} - 5 & 42 \cr}\right]$$

Likewise, an $n \times 1$ matrix is called an n-dimensional column vector. Here's a 3-dimensional column vector:

$$\left[\matrix{0 \cr 17 - e^2 \cr {\root 3 \of {617}} \cr}\right]$$

An $n \times n$ matrix is called a square matrix. For example, here is a $2 \times 2$ square matrix:

$$\left[\matrix{1 & x \cr z^2 & 32 \cr}\right]$$

Notice that by convention the number of rows is listed first and the number of columns second. This convention also applies to referring to specific elements of matrices. Consider the following matrix:

$$\left[\matrix{ 11 & -0.4 & 33 & \sqrt{2} \cr a + b & x^2 & \sin y & j - k \cr -8 & 0 & 13 & 114.71 \cr}\right]$$

The $(2, 4)^{\rm th}$ element is the element in row 2 and column 4, which is $j - k$ . (Note that the first row is row 1, not row 0, and similarly for columns.) The $(3, 3)^{\rm th}$ element is the element in row 3 and column 3, which is 13.

Equality of matrices. Two matrices are equal if they have the same dimensions and the corresponding entries are equal. For example, suppose

$$\left[\matrix{7 & 0 & 3 \cr 5 & -4 & 10 \cr}\right] = \left[\matrix{a & b & 3 \cr 5 & -4 & c \cr}\right].$$

Then if I match corresponding elements, I see that $a = 7$ , $b = 0$ , and $c = 10$ .

Definition. If R is a commutative ring, then $M(n, R)$ is the set of $n \times n$ matrices with entries in R.

Note: Some people use the notation $M_n(R)$ .

For example, $M(2,\real)$ is the set of $2 \times 2$ matrices with real entries. $M(3,\integer_5)$ is the set of $3 \times 3$ matrices with entries in $\integer_5$ .

Adding and subtracting matrices. For these examples, I'll assume that the matrices have entries in $\real$ .

You can add (or subtract) matrices by adding (or subtracting) corresponding entries.

$$\left[\matrix{1 & -1 & 0 \cr 2 & -4 & 6 \cr}\right] + \left[\matrix{7 & 1 & 3 \cr 0 & 3 & -6 \cr}\right] = \left[\matrix{1 + 7 & -1 + 1 & 0 + 3 \cr 2 + 0 & -4 + 3 & 6 + (-6) \cr}\right] = \left[\matrix{8 & 0 & 3 \cr 2 & -1 & 0 \cr}\right].$$

Matrix addition is associative --- symbolically,

$$(A + B) + C = A + (B + C).$$

This means that if you are adding several matrices, you can group them any way you wish:

$$\left(\left[\matrix{1 & -2 \cr 5 & -11 \cr}\right] + \left[\matrix{0 & 2 \cr 9 & 8 \cr}\right]\right) + \left[\matrix{4 & 3 \cr -7 & 6 \cr}\right] = \left[\matrix{1 & 0 \cr 14 & -3 \cr}\right] + \left[\matrix{4 & 3 \cr -7 & 6 \cr}\right] = \left[\matrix{5 & 3 \cr 7 & 3 \cr}\right].$$

$$\left[\matrix{1 & -2 \cr 5 & -11 \cr}\right] + \left(\left[\matrix{0 & 2 \cr 9 & 8 \cr}\right] + \left[\matrix{4 & 3 \cr -7 & 6 \cr}\right]\right) = \left[\matrix{1 & -2 \cr 5 & -11 \cr}\right] + \left[\matrix{4 & 5 \cr 2 & 14 \cr}\right] = \left[\matrix{5 & 3 \cr 7 & 3 \cr}\right].$$

Here's an example of subtraction:

$$\left[\matrix{1 & -3 \cr 2 & 0 \cr 4 & \sqrt{2} \cr}\right] - \left[\matrix{6 & 3 \cr 2 & \pi \cr 0 & 0 \cr}\right] = \left[\matrix{-5 & -6 \cr 0 & -\pi \cr 4 & \sqrt{2} \cr}\right].$$

Note that matrix addition is commutative:

$$\left[\matrix{7 & 1 & 3 \cr 0 & 3 & -6 \cr}\right] + \left[\matrix{1 & -1 & 0 \cr 2 & -4 & 6 \cr}\right] = \left[\matrix{8 & 0 & 3 \cr 2 & -1 & 0 \cr}\right].$$

Symbolically, if A and B are matrices with the same dimensions, then

$$A + B = B + A.$$

Of course, matrix subtraction is not commutative.

You can only add or subtract matrices with the same dimensions. These two matrices can't be added or subtracted:

$$\left[\matrix{1 & 2 \cr 3 & 4 \cr}\right] \quad\hbox{and}\quad \left[\matrix{0 & 0 & 0 \cr 0 & 0 & 0 \cr}\right].$$

Adding or subtracting matrices over $\integer_n$ . You add or subtract matrices over $\integer_n$ by adding or subtracting corresponding entries, but all the arithmetic is done in $\integer_n$ .

For example, here is an addition and a subtraction over $\integer_5$ :

$$\left[\matrix{1 & 2 & 4 \cr 0 & 3 & 3 \cr}\right] + \left[\matrix{4 & 3 & 0 \cr 2 & 1 & 3 \cr}\right] = \left[\matrix{ 1 + 4 & 2 + 3 & 4 + 0 \cr 0 + 2 & 3 + 1 & 3 + 3 \cr}\right] = \left[\matrix{0 & 0 & 4 \cr 2 & 4 & 1 \cr}\right].$$

$$\left[\matrix{3 & 4 \cr 2 & 0 \cr}\right] - \left[\matrix{2 & 1 \cr 4 & 1 \cr}\right] = \left[\matrix{3 - 2 & 4 - 1 \cr 2 - 4 & 0 - 1 \cr}\right] = \left[\matrix{1 & 3 \cr -2 & -1 \cr}\right] = \left[\matrix{1 & 3 \cr 3 & 4 \cr}\right].$$

Note that in the second example, there were some negative numbers in the middle of the computation, but the final answer was expressed entirely in terms of elements of $\integer_5 = \{0, 1, 2, 3, 4\}$ .

Definition. A zero matrix $\zeromatrix$ is a matrix all of whose entries are 0.

$$\left[\matrix{0 & 0 \cr 0 & 0 \cr}\right] \quad \left[\matrix{0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}\right]$$

There is an $m \times n$ zero matrix for every pair of positive dimensions m and n.

If you add the $m \times n$ zero matrix to another $m \times n$ matrix A, you get A:

$$\left[\matrix{31 & 97 \cr 24 & -53 \cr}\right] + \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right] = \left[\matrix{31 & 97 \cr 24 & -53 \cr}\right].$$

In symbols, if $\zeromatrix$ is a zero matrix and A is a matrix of the same size, then

$$A + \zeromatrix = A \quad\hbox{and}\quad \zeromatrix + A = A.$$

A zero matrix is said to be an identity element for matrix addition.

Note: At some point, I may just write "0" instead of "$\zeromatrix$ " (with the boldface) for a zero matrix, and rely on context to tell it apart from the number 0.

Multiplying matrices by numbers. You can multiply a matrix by a number by multiplying each entry by the number. Here is an example with real numbers:

$$7 \cdot \left[\matrix{3 & -3 \cr 4 & -1 \cr 0 & 2 \cr}\right] = \left[\matrix{7 \cdot 3 & 7 \cdot (-3) \cr 7 \cdot 4 & 7 \cdot (-1) \cr 7 \cdot 0 & 7 \cdot 2 \cr}\right] = \left[\matrix{21 & -21 \cr 28 & -7 \cr 0 & 14 \cr}\right].$$

Things work in the same way over $\integer_n$ , but all the arithmetic is done in $\integer_n$ . Here is an example over $\integer_5$ :

$$3 \cdot \left[\matrix{2 & 1 \cr 4 & 1 \cr}\right] = \left[\matrix{3 \cdot 2 & 3 \cdot 1 \cr 3 \cdot 4 & 3 \cdot 1 \cr}\right] = \left[\matrix{1 & 3 \cr 2 & 3 \cr}\right].$$

Notice that, as usual with $\integer_5$ , I simplified my final answer so that all the entries of the matrix were in the set $\{0, 1, 2, 3, 4\}$ .

Unlike the operations I've discussed so far, matrix multiplication (multiplying two matrices) does not work the way you might expect: You don't just multiply corresponding elements of the matrices, the way you add corresponding elements to add matrices.

To explain matrix multiplication, I'll remind you first of how you take the dot product of two vectors; you probably saw this in a multivariable calculus course. (If you're seeing this for the first time, don't worry --- it's easy!) Here's an example of a dot product of two 3-dimensional vectors of real numbers:

$$\left[\matrix{-3 & 7 & 9 \cr}\right] \left[\matrix{2 \cr 0 \cr 10 \cr}\right] = (-3) \cdot 2 + 7 \cdot 0 + 9 \cdot 10 = -6 + 0+ 90 = 84.$$

$$\hbox{\epsfysize=1.25in \epsffile{matrix-arithmetic-1.eps}}$$

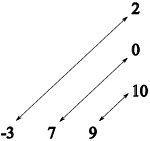
Note that the vectors must be the same size, and that the product is a number. This is actually an example of matrix multiplication, and we'll see that the result should technically be a $1 \times 1$ matrix. But for dot products, we will write

$$84 \quad\hbox{instead of}\quad \left[\matrix{84 \cr}\right].$$

If you've seen dot products in multivariable calculus, you might have seen this written this way:

$$(-3, 7, 9) \cdot (2, 0, 10) = 84.$$

But for what I'll do next, I want to distinguish between the row (first) vector and the column (second) vector.

Multiplying matrices. To compute the product $A B$ of two matrices, take the dot products of the rows of A with the columns of B. In this example, assume all the matrices have real entries.

$$\left[\matrix{{\bf 2} & {\bf 1} & {\bf 4} \cr -1 & 0 & 3 \cr}\right] \left[\matrix{{\bf 1} & 6 \cr {\bf 5} & 1 \cr {\bf 2} & -2 \cr}\right] = \left[\matrix{(2 + 5 + 8 = 15) & \cdot \cr \cdot & \cdot \cr}\right]$$

$$\left[\matrix{{\bf 2} & {\bf 1} & {\bf 4} \cr -1 & 0 & 3 \cr}\right] \left[\matrix{1 & {\bf 6} \cr 5 & {\bf 1} \cr 2 & {\bf -2} \cr}\right] = \left[\matrix{15 & (12 + 1 - 8 = 5) \cr \cdot & \cdot \cr}\right]$$

$$\left[\matrix{2 & 1 & 4 \cr {\bf -1} & {\bf 0} & {\bf 3} \cr}\right] \left[\matrix{{\bf 1} & 6 \cr {\bf 5} & 1 \cr {\bf 2} & -2 \cr}\right] = \left[\matrix{15 & 5 \cr (-1 + 0 + 6 = 5) & \cdot \cr}\right]$$

$$\left[\matrix{2 & 1 & 4 \cr {\bf -1} & {\bf 0} & {\bf 3} \cr}\right] \left[\matrix{1 & {\bf 6} \cr 5 & {\bf 1} \cr 2 & {\bf -2} \cr}\right] = \left[\matrix{15 & 5 \cr 5 & (-6 + 0 - 6 = -12) \cr}\right]$$

$$\left[\matrix{2 & 1 & 4 \cr -1 & 0 & 3 \cr}\right] \left[\matrix{1 & 6 \cr 5 & 1 \cr 2 & -2 \cr}\right] = \left[\matrix{15 & 5 \cr 5 & -12 \cr}\right].$$

This schematic picture shows how the rows of the first matrix are "dot-producted" with the columns of the second matrix to produce the 4 elements of the product:

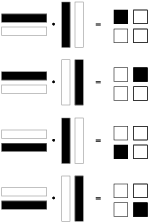
$$\hbox{\epsfysize=2in \epsffile{matrix-arithmetic-2.eps}}$$

You can see that you take the dot products of the rows of the first matrix with the columns of the second matrix.

In order for the multiplication to work, the matrices must have compatible dimensions: The number of columns in A should equal the number of rows of B. Thus, if A is an $m \times n$ matrix and B is an $n \times p$ matrix, $A B$ will be an $m \times p$ matrix. For example, this won't work:

$$\left[\matrix{ -2 & 1 & 0 & 8 \cr 1 & 11 & 13 & 9 \cr}\right] \left[\matrix{-5 & -5 \cr 2 & 13 \cr 1 & 7 \cr}\right] \quad\hbox{(Won't work!)}\quad$$

Do you see why? The rows of the first matrix have 4 entries, but the columns of the second matrix have 3 entries. You can't take the dot products, because the entries won't match up.

Here are two more examples, again using matrices with real entries:

$$\left[\matrix{-2 & 3 & 0 \cr}\right] \left[\matrix{2 & 0 \cr 9 & -4 \cr 1 & 5 \cr}\right] = \left[\matrix{23 & -12 \cr}\right].$$

$$\left[\matrix{4 & -2 \cr 1 & 1 \cr}\right] \left[\matrix{1 & 1 \cr 0 & -3 \cr}\right] = \left[\matrix{4 & 10 \cr 1 & -2 \cr}\right].$$

Here is an example with matrices in $M(2, \integer_3)$ . All the arithmetic is done in $\integer_3$ .

$$\left[\matrix{2 & 1 \cr 0 & 2 \cr}\right] \left[\matrix{1 & 2 \cr 2 & 1 \cr}\right] = \left[\matrix{4 & 5 \cr 4 & 2 \cr}\right] = \left[\matrix{1 & 2 \cr 1 & 2 \cr}\right].$$

Notice that I simplify the final result so that all the entries are in $\integer_3 = \{0, 1, 2\}$ .

If you multiply a matrix by a zero matrix, you get a zero matrix:

$$\left[\matrix{0 & 0 \cr 0 & 0 \cr}\right] \left[\matrix{9 & -3 & 43 \cr 5 & 0 & -1.2 \cr}\right] = \left[\matrix{0 & 0 & 0 \cr 0 & 0 & 0 \cr}\right].$$

In symbols, if $\zeromatrix$ is a zero matrix and A is a matrix compatible with it for multiplication, then

$$A\cdot \hbox{\bf 0} = \hbox{\bf 0} \quad\hbox{and}\quad \hbox{\bf 0}\cdot A = \hbox{\bf 0}.$$

Matrix multiplication takes a little practice, but it isn't hard. The big principle to take away is that you take the dot products of the rows of the first matrix with the columns of the second matrix. This picture of matrix multiplication will be very important for our work with matrices.

I should say something about a point I mentioned earlier: Why not multiply matrices like this?

$$\left[\matrix{4 & -3 \cr 5 & 2 \cr}\right] \left[\matrix{2 & 6 \cr 0 & 4 \cr}\right] \quad\hbox{gives}\quad \left[\matrix{4 \cdot 2 & (-3) \cdot 6 \cr 5 \cdot 0 & 2 \cdot 4 \cr}\right] \quad\hbox{?}\quad$$

You could define a matrix multiplication this way, but unfortunately, it would not be useful for applications (such as solving systems of linear equations). Or when we study the relationship between matrices and linear transformations, we'll see that the matrix multiplication we defined using dot products corresponds to the composite of transformations. So even though the "corresponding elements" definition seems simpler, it doesn't match up well with the way matrices are used.

Here's a preview of how matrices are related to systems of linear equations.

Example. Write the system of equations which correspond to the matrix equation

$$\left[\matrix{2 & 3 & 0 \cr -1 & 5 & 17 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{13 \cr 0 \cr}\right].$$ Multiply out the left side:

$$\left[\matrix{2 a + 3 b \cr -a + 5 b + 17 c \cr}\right] = \left[\matrix{13 \cr 0 \cr}\right].$$

Two matrices are equal if their corresponding entries are equal, so equate corresponding entries:

$$\matrix{ 2 a & + & 3 b & & & = & 13 \cr -a & + & 5 b & + & 17 c & = & 0 \cr}\quad\halmos$$

Example. Write the following system of linear equations as a matrix multiplication equation:

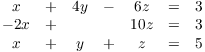
$$\matrix{ x & + & 4y & - & 6 z & = & 3 \cr -2 x & + & & & 10 z & = & 3 \cr x & + & y & + & z & = & 5 \cr}$$

Take the 9 coefficients of the variables x, y, and z on the left side and make them into a $3 \times 3$ matrix. Put the variables into a 3-dimensional column vector. Make the 3 numbers on the right side into a 3-dimensional column vectors. Here's what we get:

$$\left[\matrix{ 1 & 4 & -6 \cr -2 & 0 & 10 \cr 1 & 1 & 1 \cr}\right] \left[\matrix{x \cr y \cr z \cr}\right] = \left[\matrix{3 \cr 3 \cr 5 \cr}\right].$$

Work out the multiplication on the left side of this equation and you'll see how this represents the original system.

This is really important! It allows us to represent a system of equations as a matrix equation. Eventually, we'll figure out how to solve the original system by working with the matrices.

Identity matrices. There are special matrices which serve as identities for multiplication: The $n \times n$ identity matrix is the square matrices with 1's down the main diagonal --- the diagonal running from northwest to southeast --- and 0's everywhere else. For example, the $3 \times 3$ identity matrix is

$$I = \left[\matrix{1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right].$$

If I is the $n \times n$ identity and A is a matrix which is compatible for multiplication with A, then

$$A I = A \quad\hbox{and}\quad I A = A.$$

For example,

$$\left[\matrix{ 3 & -7 & 10 \cr \noalign{\vskip2pt} \pi & \dfrac{1}{2} & -1.723 \cr \noalign{\vskip2pt} 0 & 19 & 712 \cr}\right] \left[\matrix{1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] = \left[\matrix{ 3 & -7 & 10 \cr \noalign{\vskip2pt} \pi & \dfrac{1}{2} & -1.723 \cr \noalign{\vskip2pt} 0 & 19 & 712 \cr}\right].$$

Matrix multiplication obeys some of the algebraic laws you're familiar with. For example, matrix multiplication is associative: If A, B, and C are matrices and their dimensions are compatible for multiplication, then

$$(A B)C = A(B C).$$

However, matrix multiplication is not commutative in general. That is, $AB \ne BA$ for all matrices A, B.

One trivial way to get a counterexample is to let A be $3 \times 5$ and let B be $5 \times 3$ . Then $A B$ is $3 \times 3$ while $B A$ is $5 \times 5$ . Since $A B$ and $B A$ have different dimensions, they can't be equal.

However, it's easy to come up with counterexamples even when $A B$ and $B A$ have the same dimensions. For example, consider the following matrices in $M(2, \real)$ :

$$A = \left[\matrix{1 & -1 \cr 2 & 3 \cr}\right] \quad\hbox{and}\quad B = \left[\matrix{1 & 0 \cr 4 & 1 \cr}\right].$$

Then you can check by doing the multiplications that

$$A B = \left[\matrix{-3 & -1 \cr 14 & 3 \cr}\right] \quad\hbox{but}\quad B A = \left[\matrix{1 & -1 \cr 6 & -1}\right].$$

Many of the properties of matrix arithmetic are things you'd expect --- for example, that matrix addition is commutative, or that matrix multiplication is associative. You should pay particular attention when things don't work the way you'd expect, and this is such a case. It is very significant that matrix multiplication is not always commutative.

Transposes. If A is a matrix, the transpose $A^T$ of A is obtained by swapping the rows and columns of A. For example,

$$\left[\matrix{1 & 2 & 3 \cr 4 & 5 & 6 \cr}\right]^T = \left[\matrix{1 & 4 \cr 2 & 5 \cr 3 & 6 \cr}\right].$$

Notice that the transpose of an $m \times n$ matrix is an $n \times m$ matrix.

Example. Consider the following matrices with real entries:

$$A = \left[\matrix{1 & 0 & 1 & 2 \cr 2 & 1 & -1 & 0 \cr}\right], \quad B = \left[\matrix{c & c \cr 1 & 1 \cr}\right], \quad C = \left[\matrix{0 & 1 \cr 2 & -1 \cr 0 & 0 \cr 1 & 1 \cr}\right].$$

(a) Compute $C B + A^T$ .

(b) Compute $A C - 2 B$ .

(a)

$$C B + A^T = \left[\matrix{0 & 1 \cr 2 & -1 \cr 0 & 0 \cr 1 & 1 \cr}\right] \left[\matrix{c & c \cr 1 & 1 \cr}\right] + \left[\matrix{1 & 0 & 1 & 2 \cr 2 & 1 & -1 & 0 \cr}\right]^T = \left[\matrix{1 & 1 \cr 2 c - 1 & 2 c - 1 \cr 0 & 0 \cr c + 1 & c + 1 \cr}\right] + \left[\matrix{1 & 2 \cr 0 & 1 \cr 1 & -1 \cr 2 & 0 \cr}\right] = \left[\matrix{2 & 3 \cr 2 c - 1 & 2 c \cr 1 & -1 \cr c + 3 & c + 1 \cr}\right].\quad\halmos$$

(b)

$$A C - 2 B = \left[\matrix{1 & 0 & 1 & 2 \cr 2 & 1 & -1 & 0 \cr}\right] \left[\matrix{0 & 1 \cr 2 & -1 \cr 0 & 0 \cr 1 & 1 \cr}\right] - 2 \left[\matrix{c & c \cr 1 & 1 \cr}\right] = \left[\matrix{2 & 3 \cr 2 & 1 \cr}\right] - \left[\matrix{2 c & 2 c \cr 2 & 2 \cr}\right] = \left[\matrix{2 - 2 c & 3 - 2 c \cr 0 & -1 \cr}\right].\quad\halmos$$

The inverse of a matrix. The inverse of an $n \times n$ matrix A is a matrix $A^{-1}$ which satisfies

$$A A^{-1} = I \quad\hbox{and}\quad A^{-1} A = I.$$

There is no such thing as matrix division in general, because some matrices do not have inverses. But if A has an inverse, you can simulate division by multiplying by $A^{-1}$ . This is often useful in solving matrix equations.

An $n \times n$ matrix which does not have an inverse is called singular.

We'll discuss matrix inverses and how you find them in detail later. For now, here's a formula that we'll use frequently.

Proposition. Consider the following matrix with entries in a commutative ring with identity R.

$$A = \left[\matrix{a & b \cr c & d \cr}\right].$$

Suppose that $a d - b c$ is invertible in R. Then the inverse of A is

$$A^{-1} = (a d - b c)^{-1} \left[\matrix{d & -b \cr -c & a \cr}\right].$$

Note: The number $a d - b c$ is called the determinant of the matrix. We'll discuss determinants later.

Remember that not every element of a commutative ring with identity has an inverse. For example, $4^{-1}$ is undefined in $\integer_6$ . If we're dealing with real numbers, then $a d - b c$ has a multiplicative inverse if and only if it's nonzero.

Proof. To show that the formula gives the inverse of A, I have to check that $A A^{-1} = I$ and $A^{-1} A = I$ :

$$A A^{-1} = \left[\matrix{a & b \cr c & d \cr}\right] \cdot (a d - b c)^{-1} \left[\matrix{d & -b \cr -c & a \cr}\right] = (a d - b c)^{-1} \left[\matrix{a d - b c & 0 \cr 0 & a d - b c}\right] = \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right],$$

$$A^{-1} A = (a d - b c)^{-1} \left[\matrix{d & -b \cr -c & a \cr}\right] \left[\matrix{a & b \cr c & d \cr}\right] = (a d - b c)^{-1} \left[\matrix{a d - b c & 0 \cr 0 & a d - b c \cr}\right] = \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right].$$

This proves that the formula gives the inverse of a $2 \times 2$ matrix.

Here's an example of this formula for a matrix with real entries. Notice that $3 \cdot (-1) - 5 \cdot (-2) = 7$ . So

$$\left[\matrix{3 & 5 \cr -2 & -1 \cr}\right]^{-1} = \dfrac{1}{7} \cdot \left[\matrix{-1 & -5 \cr 2 & 3 \cr}\right].$$

(If I have a fraction outside a matrix, I may choose not to multiply it into the matrix to make the result look nicer. Generally, if there is an integer outside a matrix, I will multiply it in.)

Recall that a matrix which does not have an inverse is called singular. Suppose we have a real matrix

$$A = \left[\matrix{a & b \cr c & d \cr}\right].$$

The formula above will produce an inverse if $a d - b c$ is invertible, which for real numbers means $a d - b c \ne 0$ . So the matrix is singular if $a d - b c = 0$ .

Example. For what values of x is the following real matrix singular?

$$\left[\matrix{x - 1 & 3 \cr 4 & x - 5 \cr}\right]$$

The matrix is singular --- not invertible --- if

$$a d - b c = (x - 1)(x - 5) - (3)(4) = 0.$$

Solve for x:

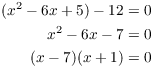
$$\eqalign{ (x^2 - 6x + 5) - 12 & = 0 \cr x^2 - 6x - 7 & = 0 \cr (x - 7)(x + 1) & = 0 \cr}$$

This gives $x = 7$ or $x = -1$ . The matrix is singular for $x = 7$ and for $x = -1$ .

Be careful! The following matrix is singular over $\integer_6$ :

$$\left[\matrix{5 & 1 \cr 3 & 1 \cr}\right]$$

However, its determinant is $5 \cdot 1 - 1 \cdot 3 = 2$ , which is nonzero. The point is that 2 is not invertible in $\integer_6$ , even though it's nonzero.

Example. (a) Find $2^{-1}$ in $\integer_5$ .

(b) Find the inverse of the following matrix over $\integer_5$ .

$$\left[\matrix{3 & 1 \cr 1 & 1 \cr}\right]$$

(You should multiply any numbers outside the matrix into the matrix, and simplify all the numbers in the final answer in $\integer_5$ .)

(a) Since $2 \cdot 3 = 6 = 1$ in $\integer_5$ , I have $2^{-1} = 3$ .

(b) First, the determinant is $3 \cdot 1 - 1 \cdot 1 = 2$ . I saw in (a) that $2^{-1} = 3$ . So

$$\left[\matrix{3 & 1 \cr 1 & 1 \cr}\right]^{-1} = 2^{-1} \cdot \left[\matrix{1 & -1 \cr -1 & 3 \cr}\right] = 3 \cdot \left[\matrix{1 & -1 \cr -1 & 3 \cr}\right] =$$

$$\left[\matrix{3 & -3 \cr -3 & 9 \cr}\right] = \left[\matrix{3 & 2 \cr 2 & 4 \cr}\right].$$

I reduced all the numbers in $\integer_5$ at the last step; for example, $-3 = 2$ in $\integer_5$ . As a check,

$$\left[\matrix{3 & 2 \cr 2 & 4 \cr}\right] \left[\matrix{3 & 1 \cr 1 & 1 \cr}\right] = \left[\matrix{11 & 5 \cr 10 & 6 \cr}\right] = \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right].$$

That is, when I multiply the inverse and the original matrix, I get the identity matrix. Check for yourself that it also works if I multiply them in the opposite order.

We'll discuss solving systems of linear equations later, but here's an example of this which puts a lot of the ideas we've discussed together.

Example. ( Solving a system of equations) Solve the following system over $\real$ for x and y using the inverse of a matrix.

$$\matrix{x & + & 3y & = & 7 \cr 2x & - & 2y & = & -2 \cr}$$

Write the equation in matrix form:

$$\left[\matrix{1 & 3 \cr 2 & -2 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{7 \cr -2 \cr}\right].$$

Using the formula for the inverse of a $2 \times 2$ matrix, I find that

$$\left[\matrix{1 & 3 \cr 2 & -2 \cr}\right]^{-1} = -\dfrac{1}{8} \left[\matrix{-2 & -3 \cr -2 & 1 \cr}\right].$$

Multiply both sides by the inverse matrix:

$$-\dfrac{1}{8} \left[\matrix{-2 & -3 \cr -2 & 1 \cr}\right] \left[\matrix{1 & 3 \cr 2 & -2 \cr}\right] \left[\matrix{x \cr y \cr}\right] = -\dfrac{1}{8} \left[\matrix{-2 & -3 \cr -2 & 1 \cr}\right] \left[\matrix{7 \cr -2 \cr}\right].$$

On the left, the square matrix and its inverse cancel, since they multiply to I. (Do you see how that is like "dividing by the matrix"?) On the right,

$$-\dfrac{1}{8} \left[\matrix{-2 & -3 \cr -2 & 1 \cr}\right] \left[\matrix{7 \cr -2 \cr}\right] = \left[\matrix{1 \cr 2 \cr}\right].$$

Therefore,

$$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{1 \cr 2 \cr}\right].$$

The solution is $x = 1$ , $y = 2$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga