Sums and Products

In this section, I'll review the notation for sums and products.

Addition and multiplication are binary operations: They operate on two numbers at a time. If you want to add or multiply more than two numbers, you need to group the numbers so that you're only adding or multiplying two at once.

Addition and multiplication are associative, so it should not matter how I group the numbers when I add or multiply. Now associativity holds for three numbers at a time; for instance, for addition,

$$a + (b + c) = (a + b) + c.$$

But why does this work for (say) two ways of grouping a sum of 100 numbers?

It turns out that, using induction, it's possible to prove that any two ways of grouping a sum or product of n numbers, for $n \ge 3$ , give the same result.

Taking this for granted, I can define the sum of a list of numbers $\{a_1, a_2, \ldots a_n\}$ recursively as follows.

A sum of a single number is just the number:

$$\sum_{i = 1}^1 a_i = a_1.$$

I know how to add two numbers:

$$\sum_{i = 1}^2 a_i = a_1 + a_2.$$

To add n numbers for $n > 2$ , I add the first $n - 1$ of them (which I assume I already know how to do), then add the $n^{\rm th}$ :

$$\sum_{i = 1}^n a_i = \sum_{i = 1}^{n - 1} a_i + a_n.$$

Note that this is a particular way of grouping the n summands: Make one group with the first $n - 1$ , and add it to the last term. By associativity (as noted above), this way of grouping the sum should give the same result as any other way.

Therefore, I might as well omit parentheses and write

$$\sum_{i = 1}^n a_i = a_1 + a_2 + \cdots + a_n.$$

The product of a list of numbers $\{a_1, a_2, \ldots a_n\}$ is defined recursively in a similar way.

A product of a single number is just the number:

$$\prod_{i = 1}^1 a_i = a_1.$$

I know how to multiply two numbers:

$$\prod_{i = 1}^2 a_i = a_1 \cdot a_2.$$

To multiply n numbers for $n > 2$ , I multiply the first $n - 1$ of them (which I assume I already know how to do), then multiply the $n^{\rm th}$ :

$$\prod_{i = 1}^n a_i = \prod_{i = 1}^{n - 1} a_i \cdot a_n.$$

Again, I can drop the parentheses and write

$$\prod_{i = 1}^n a_i = a_1 \cdot a_2 \cdot \cdots \cdot a_n.$$

Remark. Some people define the sum and product of no numbers as follows: The sum of no numbers (sometimes called the empty sum is defined to be 0, and the product of no numbers (sometimes called the empty product) is defined to be 1. These definitions are useful when you're taking the sum or product of numbers in a set, rather than the sum or product of numbers indexed by a range of consecutive integers.

For example, suppose $S = \{1, 4, 9, 13\}$ . Then to use summation notation to write the sum of the squares of the elements of S, you might write

$$\sum_{x \in S} x^2 \quad\hbox{to mean}\quad 1^2 + 4^2 + 9^2 + 13^2.$$

Similarly, to write the product of the reciprocals of the numbers in S, you might write

$$\prod_{x \in S} \dfrac{1}{x} \quad\hbox{to mean}\quad \dfrac{1}{1} \cdot \dfrac{1}{4} \cdot \dfrac{1}{9} \cdot \dfrac{1}{13}.$$

If the set containing the elements of the sum or product varies in a discussion, it might happen that the containing set is empty. Using the definitions for an empty sum or an empty product allows for this case. For instance,

$$\sum_{x \in \emptyset} x^2 = 0.$$

That is, the sum of the squares of the elements of the empty set is 0.

The following properties and those for products which are given below are fairly obvious, but careful proofs require induction.

Proposition. ( Properties of sums)

(a) $\displaystyle \sum_{i = 1}^n (a_i + b_i) = \sum_{i = 1}^n a_i + \sum_{i = 1}^n b_i$ .

(b) $\displaystyle \sum_{i = 1}^n c \cdot a_i = c \cdot \sum_{i = 1}^n a_i$ .

(c) $\displaystyle \sum_{i = 1}^n c = n \cdot c$ .

Proof. I'll prove (c) as an example. I'll use induction. For $n = 1$ , the left side is $\displaystyle \sum_{i = 1}^1 c = c$ and the right side is $1 \cdot c = c$ . The result holds for $n = 1$ .

Assume that the result holds for n:

$$\sum_{i = 1}^n c = n \cdot c.$$

Then for $n + 1$ , I have

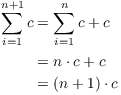
$$\eqalign{ \sum_{i = 1}^{n + 1} c & = \sum_{i = 1}^n c + c \cr & = n \cdot c + c \cr & = (n + 1) \cdot c \cr}$$

The first equality used the recursive definition of a sum. The second equality follows from the induction hypothesis. The final equality is just basic algebra.

Properties (a) and (b) can also be proved using induction.

Example. Compute the following sums:

(a) $\displaystyle \sum_{i = 1}^4 i^2$ .

(b) $\displaystyle \sum_{i = 2}^6 i \cdot b_i$ .

(c) $\displaystyle \sum_{j = 1}^{50} 4$ .

(d) $\displaystyle \sum_{i = 1}^n (a_i + c)$ , where c is a constant.

(a)

$$\sum_{i = 1}^4 i^2 = 1^2 + 2^2 + 3^2 + 4^2 = 30.\quad\halmos$$

(b)

$$\sum_{i = 2}^6 i \cdot b_i = 2 b_2 + 3 b_3 + 4 b_4 + 5 b_5 + 6 b_6.$$

Note that sums need not start indexing at 1.

(c)

$$\sum_{k = 1}^{50} 4 = 50 \cdot 4 = 200.$$

Note that the summation variable can be anything that you want.

(d)

$$\sum_{i = 1}^n (a_i + c) = \sum_{i = 1}^n a_i + \sum_{i = 1}^n c = \sum_{i = 1}^n a_i + n \cdot c.\quad\halmos$$

Example. Compute the exact value of $\displaystyle \sum_{n = 1}^{50} \dfrac{\sqrt{n + 2} - \sqrt{n + 1}}{\sqrt{n^2 + 3 n + 2}}$ .

Note that

$$\dfrac{\sqrt{n + 2} - \sqrt{n + 1}}{\sqrt{n^2 + 3 n + 2}} = \dfrac{\sqrt{n + 2} - \sqrt{n + 1}}{\sqrt{(n + 1)(n + 2)}} = \dfrac{1}{\sqrt{n + 1}} - \dfrac{1}{\sqrt{n + 2}}.$$

So

$$\sum_{n = 1}^{50} \dfrac{\sqrt{n + 2} - \sqrt{n + 1}}{\sqrt{n^2 + 3 n + 2}} = \sum_{n = 1}^{50} \left(\dfrac{1}{\sqrt{n + 1}} - \dfrac{1}{\sqrt{n + 2}}\right).$$

I'll write out a few of the terms:

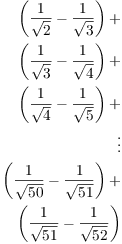
$$\eqalign{ \left(\dfrac{1}{\sqrt{2}} - \dfrac{1}{\sqrt{3}}\right) + \cr \left(\dfrac{1}{\sqrt{3}} - \dfrac{1}{\sqrt{4}}\right) + \cr \left(\dfrac{1}{\sqrt{4}} - \dfrac{1}{\sqrt{5}}\right) + \cr \vdots \cr \left(\dfrac{1}{\sqrt{50}} - \dfrac{1}{\sqrt{51}}\right) + \cr \left(\dfrac{1}{\sqrt{51}} - \dfrac{1}{\sqrt{52}}\right) \cr}$$

Most of the terms cancel in pairs, with the negative term in one expression cancelling with the positive term in the next expression. Only the first term and the last term are left, and they give the value of the sum:

$$\sum_{n = 1}^{50} \dfrac{\sqrt{n + 2} - \sqrt{n + 1}}{\sqrt{n^2 + 3 n + 2}} = \dfrac{1}{\sqrt{2}} - \dfrac{1}{\sqrt{52}}.$$

This is an example of a telescoping sum.

Proposition. ( Properties of products)

(a) $\displaystyle \prod_{i = 1}^n a_i b_i = \left(\prod_{i = 1}^n a_i\right)\left(\prod_{i = 1}^n b_i\right)$ .

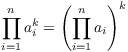(b) $\displaystyle \prod_{i = 1}^n a_i^k = \left(\prod_{i = 1}^n a_i\right)^k$ .

(c) $\displaystyle \prod_{i = 1}^n c = c^n$ .

Proof. I'll prove (a) by way of example. The proof will use induction on n.

For $n = 1$ , the left side is $\displaystyle \prod_{i = 1}^1 a_i b_i = a_1 b_1$ . The right side is $\displaystyle \left(\prod_{i = 1}^1 a_i\right)\left(\prod_{i = 1}^1 b_i\right) = a_1 b_1$ . The result holds for $n = 1$ .

Assume that the result holds for n:

$$\prod_{i = 1}^n a_i b_i = \left(\prod_{i = 1}^n a_i\right)\left(\prod_{i = 1}^n b_i\right).$$

Then for $n + 1$ , I have

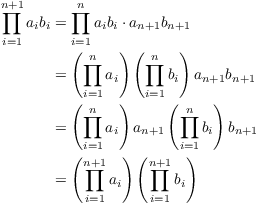
$$\eqalign{ \prod_{i = 1}^{n + 1} a_i b_i & = \prod_{i = 1}^n a_i b_i \cdot a_{n + 1} b_{n + 1} \cr & = \left(\prod_{i = 1}^n a_i\right) \left(\prod_{i = 1}^n b_i\right) a_{n + 1} b_{n + 1} \cr & = \left(\prod_{i = 1}^n a_i\right) a_{n + 1} \left(\prod_{i = 1}^n b_i\right) b_{n + 1} \cr & = \left(\prod_{i = 1}^{n + 1} a_i\right) \left(\prod_{i = 1}^{n + 1} b_i\right) \cr}$$

The first equality follows from the recursive definition of a product. The second equality uses the induction hypothesis. The third equality comes from commutativity of multiplication. And the fourth equality is a result of the recursive definition of a product again.

Properties (b) and (c) can also be proved by induction.

Example. Compute the following products:

(a) $\displaystyle \prod_{n = 1}^4 e^n$ .

(b) $\displaystyle \prod_{i = 1}^n (c a_i)^2$ , where c is a constant.

(c) $\displaystyle \prod_{k = 1}^{20} 5$ .

(a)

$$\prod_{n = 1}^4 e^n = e \cdot e^2 \cdot e^3 \cdot e^4 = e^{10}.\quad\halmos$$

(b)

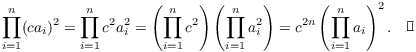
$$\prod_{i = 1}^n (c a_i)^2 = \prod_{i = 1}^n c^2 a_i^2 = \left(\prod_{i = 1}^n c^2 \right)\left(\prod_{i = 1}^n a_i^2 \right) = c^{2 n} \left(\prod_{i = 1}^n a_i \right)^2.\quad\halmos$$

(c)

$$\prod_{k = 1}^{20} 5 = 5^{20}.\quad\halmos$$

Example. Compute the exact value of $\displaystyle \prod_{n = 1}^{50} \left(1 + \dfrac{4}{n} + \dfrac{4}{n^2}\right)$ .

Note that

$$1 + \dfrac{4}{n} + \dfrac{4}{n^2} = \dfrac{n^2 + 4 n + 4}{n^2} = \dfrac{(n + 2)^2}{n^2}.$$

So

$$\prod_{n = 1}^{50} \left(1 + \dfrac{4}{n} + \dfrac{4}{n^2}\right) = \prod_{n = 1}^{50} \dfrac{(n + 2)^2}{n^2}.$$

I'll write out a few of the terms:

$$\dfrac{3^2}{1^2} \cdot \dfrac{4^2}{2^2} \cdot \dfrac{5^2}{3^2} \cdot \dfrac{6^2}{4^2} \cdot \cdots \cdot \dfrac{50^2}{48^2} \cdot \dfrac{51^2}{49^2} \cdot \dfrac{52^2}{50^2}$$

Most of the terms in the numerators cancel with the terms in the denominators "two fractions ahead". Only the first two denominators and the last two numerators don't cancel, and they give the value of the product:

$$\prod_{n = 1}^{50} \left(1 + \dfrac{4}{n} + \dfrac{4}{n^2}\right) = \dfrac{51^2 \cdot 52^2}{1^2 \cdot 2^2} = 1758276.$$

This is an example of a telescoping product.

If n is a positive integer, $n!$ (read n-factorial) is the product of the integers from 1 to n:

$$n! = \prod_{k=1}^n k = 1 \cdot 2 \cdot \cdots \cdot n.$$

For example,

$$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120.$$

By convention, $0!$ is defined to be 1. This definition agrees with the extension of factorials using the Gamma function, described below. It also is the appropriate definition when factorials come up in binomial coefficients.

Note that

$$n! = 1 \cdot 2 \cdot \cdots \cdot (n - 1) \cdot n = (n - 1)! \cdot n.$$

There is a way of extending the definition of factorials to positive real numbers (so that, for instance, $\dfrac{1}{2}!$ is defined). The Gamma function is defined by

$$\Gamma(x) = \int_0^\infty e^{-t} t^{x-1}\,dt \quad\hbox{for}\quad x > 0.$$

(Note that x here is a real number.) If n is a positive integer,

$$\Gamma(n + 1) = n!.$$

Here's a graph of the Gamma function:

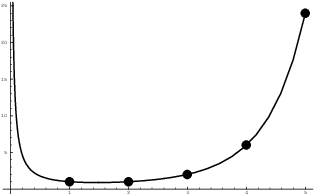
$$\hbox{\epsfysize=1.75in \epsffile{sums-and-products1.eps}}$$

I've placed dots at the points $(n, (n - 1)!)$ so you can see that the Gamma function really goes through the factorial points. Note also that $\Gamma(1) = 1$ . But if I plug $n = 0$ into the formula above, I get $\Gamma(0 + 1) = 0!$ , i.e. $\Gamma(1) = 0!$ . Thus, $0! = 1$ , which is the convention I mentioned earlier.

Example. Evaluate $\Gamma(5)$ using the integral definition.

$$\Gamma(5) = \int_0^\infty t^4 e^{-t}\,dt = \lim_{b \to \infty} \int_0^b t^4 e^{-t}\,dt.$$

Do the antiderrivative by parts:

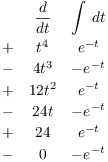
$$\matrix{ & \displaystyle \der {} t & \displaystyle \int\,dt \cr \noalign{\vskip2pt} + & t^4 & e^{-t} \cr \noalign{\vskip2pt} - & 4 t^3 & -e^{-t} \cr \noalign{\vskip2pt} + & 12 t^2 & e^{-t} \cr \noalign{\vskip2pt} - & 24 t & -e^{-t} \cr \noalign{\vskip2pt} + & 24 & e^{-t} \cr \noalign{\vskip2pt} - & 0 & -e^{-t} \cr}$$

$$\int t^4 e^{-t}\,dt = -t^4 e^{-t} - 4 t^3 e^{-t} - 12 t^2 e^{-t} - 24 t e^{-t} - 24 e^{-t} + c.$$

So the definite integral is

$$\lim_{b \to \infty} \left(-b^4 e^{-b} - 4 b^3 e^{-b} - 12 b^2 e^{-b} - 24 b e^{-b} - 24 e^{-b} + 24\right) = 24.$$

All the b-terms go to 0, because

$$\lim_{b \to \infty} b^n e^{-b} = 0 \quad\hbox{for}\quad n \ge 0.\quad\halmos$$

Note that $24 = 4!$ , so $\Gamma(5) = 4!$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga