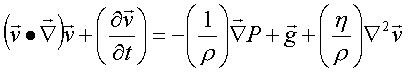
The rate at which an incompressible viscous fluid flows through a cylindrical pipe can be calculated from the Navier-Stokes equation. The result is called Poiseuille's Law. We begin by calculating the velocity field of such a flow.
We expect the velocity field to be zero at the boundaries, where it touches the walls of the pipe. Just inside the boundary, we expect the steady state velocity to be same, all the way around the circumference. That is we expect the velocity field to have circular symmetry, with surfaces of equal velocity being cylinders parallel to the axis of the pipe. (Compare this with the planes of equal velocity between two flat plates.)
In other words, we assume laminar flow, with the layers being cylinders co-axial with the pipe. (Note that these cylinders also contain the streamlines for the flow.) As a reminder, the Navier-Stokes equation is repeated below
| Coordinate system for steady state flow in a cylindrical pipe, |
| with cylindrical surfaces of equal velocity. |
We are seeking a steady state solution, so the time derivative of the velocity field on the left side of the Navier-Stokes equation is zero.
In addition, since the streamlines have constant velocity, there is no
acceleration associated with change of position of our sample volume. This
means that the
term is zero.
Finally, to keep the calculation simple, we assume that the gravitational
effects are small, and set
. The
Navier-Stokes equation becomes
with
We will work on this equation in cylindrical coordinates, with the x-axis down the axis of the pipe, as sketched in the figure. For cylindrical coordinates we accept as a gift from mathematicians the following expressions for our derivative operators:
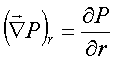
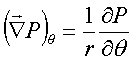
and
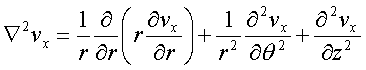
The assumption of cylindrical symmetry, plus the assumption that the
(symmetry-breaking) gravitational field is zero, means that our fields must be
independent of the angle
, so
derivatives with respect to
are zero.
Note well that
is not a
function of
or
,
is still
allowed to be a function of
.
We have already argued that surfaces of constant velocity are cylinders
parallel to the x-axis. This means that derivatives of the velocity with
respect to
must be zero. The
component of
the Navier-Stokes equation reduces to:
or
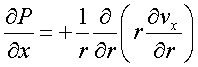
Since the only non-zero component of the velocity is the x component, the other two components of the Navier-Stokes equation are even simpler:
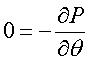
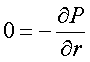
These two equations tell us that the pressure is a function of only x.
Since the left side of
is independent of
, the right
side (a function of
only)
must be constant.
Let us guess an expression for the velocity. We will try the polynomial form
,
since higher powers of
will not
differentiate to a constant.
( A more complete treatment shows that the proper form is
. Since we
must allow
,
and the logarithm of zero goes to infinity, it cannot appear in our solution.
See "Fluid Mechanics," by Pijush K. Kundu, Academic press, 1990,
p270.)
| This velocity field for a pipe of radius R is not a steady state |
| solution because its downstream velocity at the center will increase. |
Our solution has the form of a parabola, as sketched in the figure. In
general the parabola is "offset" by the term linear in
, as shown.
In this case the velocity field is as sketched. The viscous force on the small
volume is in the downstream direction, from both above and below. Since the net
force is not zero, the small volume must accelerate. This violates our
requirement of a steady state solution.
Only if
will the velocity field avoid the "kink" that causes an acceleration
at the center of the pipe.
We have another condition to apply: The velocity field must be zero when
where
is the radius
of the pipe. This means that
, so
that
| Parabolic velocity field for steady state viscous flow in a |
| cylindrical pipe of radius R. |
Our guess for the velocity has the form:
.
Plugging this into the x component of the Navier-Stokes equation gives
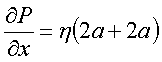
so that
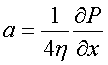
After some algebra, we find
 .
.
Return to index.
Return to survey.
Go forward to Poiseuille's Law denouement.