Metric Spaces

Definition. If X is a set, a metric on X is a function $d: X \times X \to \real$ such that:

(a) $d(x,y) \ge 0$ for all $x, y \in X$ ; $d(x,y) = 0$ if and only if $x = y$ .

(b) $d(x,y) = d(y,x)$ for all $x, y \in X$ .

(c) ( Triangle Inequality) For all $x, y, z \in X$ ,

$$d(x,y) + d(y,z) \ge d(x,z).$$

Lemma. Let X be a set with a metric, and consider the set of open balls of the form

$$B(x; \epsilon) = \left\{y \in X \mid d(x,y) < \epsilon\right\}.$$

The set $\{B(x; \epsilon)\}$ for all $x \in X$ and all $\epsilon > 0$ forms a basis for a topology on X.

Proof. If $x \in X$ , then $x \in B(x; 1)$ .

Suppose $B(x_1; \epsilon_1)$ and $B(x_2; \epsilon_2)$ are open balls. Let $x \in B(x_1; \epsilon_1) \cap B(x_2; \epsilon_2)$ .

Let

$$\epsilon = \min(\epsilon_1 - d(x,x_1), \epsilon_2 - d(x,x_2)).$$

Then $x \in B(x; \epsilon) \subset B(x_1; \epsilon_1) \cap B(x_2; \epsilon_2)$ . Therefore, the collection of open balls forms a basis.

Definition. If X is a set with a metric, the metric topology on X is the topology generated by the basis consisting of open balls $B(x; \epsilon)$ , where $x \in X$ and $\epsilon > 0$ .

A metric space consists of a set X together with a metric d, where X is given the metric topology induced by d.

Remark. In generating a metric topology, it suffices to consider balls of rational radius.

Example. Let $x = (x_1, \ldots, x_n)$ and $y = (y_1, \ldots, y_n)$ be elements of $\real^n$ , and define

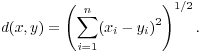
$$d(x,y) = \left(\sum_{i=1}^n (x_i - y_i)^2\right)^{1/2}.$$

This gives the standard or Euclidean metric on $\real^n$ .

It is clear that $d(x,y) \ge 0$ and that $d(x,x) = 0$ for all $x, y \in \real^n$ . If $x = (x_1, \ldots, x_n)$ and $y = (y_1, \ldots, y_n)$ and $d(x,y) = 0$ , then

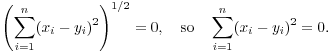
$$\left(\sum_{i=1}^n (x_i - y_i)^2\right)^{1/2} = 0, \quad\hbox{so}\quad \sum_{i=1}^n (x_i - y_i)^2 = 0.$$

This is only possible if $(x_i - y_i)^2 = 0$ for all i, and this in turn implies that $x_i = y_i$ for all i. Therefore, $x = y$ .

It is obvious that $d(x,y) = d(y,x)$ for all $x, y \in \real^n$ .

Note that $d(x,y) = |x - y|$ , where $|\cdot|$ is the standard norm which gives the length of a vector. Now $|u|^2 = u\cdot u$ , where $\cdot$ denotes the dot product in $\real^n$ . By standard properties of the dot product,

$$|u + v|^2 = (u + v)\cdot (u + v) = u\cdot u + 2u\cdot v + v\cdot v = |u|^2 + 2u\cdot v + |v|^2 \le |u|^2 + 2|u||v| + |v|^2 = (|u| + |v|)^2.$$

(The inequality follows from the Schwarz inequality $|u\cdot v| \le |u||v|$ .) Then

$$|u + v| \le |u| + |v|.$$

Now let $u = x - y$ and $v = y - z$ . Then

$$|x - z| \le |x - y| + |y - z|, \quad\hbox{or}\quad d(x,z) \le d(x,y) + d(y,z).$$

Here is a proof of the Schwarz inequality in case you ahven't seen it. Given $u = (u_1, \ldots, u_n), v = (v_1, \ldots, v_n) \in \real^n$ , I want to show that $|u\cdot v| \le |u||v|$ ; I'll show that $|u\cdot v|^2 \le |u|^2|v|^2$ , and the result will follow by taking square roots.

Set $A = |u|^2$ , $C = |v|^2$ , and $B = |u\cdot v|$ . I want to show that $B^2 \le AC$ .

If $A = 0$ , then $u = 0$ , and the result is obvious. Assume then that $A > 0$ . For all $x \in \real$ ,

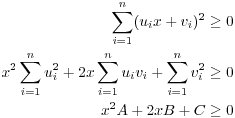
$$\eqalign{\sum_{i=1}^n (u_ix + v_i)^2 &\ge 0 \cr x^2 \sum_{i=1}^n u_i^2 + 2x \sum_{i=1}^n u_iv_i + \sum_{i=1}^n v_i^2 &\ge 0 \cr x^2 A + 2xB + C &\ge 0 \cr}$$

Take $x = -\dfrac{B}{A}$ . The last inequality yields

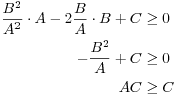
$$\eqalign{\dfrac{B^2}{A^2}\cdot A - 2\dfrac{B}{A}\cdot B + C &\ge 0 \cr -\dfrac{B^2}{A} + C &\ge 0 \cr AC &\ge C \cr}$$

This completes the proof of the Schwarz inequality.

Thus, the standard metric on $\real^n$ satisfies the axioms for a metric. Obviously, the metric topology is just the standard topology.

Lemma. ( Comparison Lemma for Metric Topologies) Let d and $d'$ be metrics on X inducing topologies ${\cal T}$ and ${\cal T}'$ . ${\cal T}$ is finer than ${\cal T}'$ if and only if for all $x \in X$ and $\epsilon > 0$ , there is a $\delta > 0$ such that $B_d(x; \delta) \subset B_{d'}(x; \epsilon)$ .

Proof. Suppose first that ${\cal T}' \subset {\cal T}$ . Let $x \in X$ , and let $\epsilon > 0$ . $B_{d'}(x; \epsilon)$ is open in ${\cal T}'$ , so it's open in ${\cal T}$ . Since the open d-balls form a basis for ${\cal T}$ , there is an open ball $B_d(x; \delta)$ such that

$$x \in B_d(x; \delta) \subset B_{d'}(x; \epsilon).$$

Conversely, suppose that for all $x \in X$ and $\epsilon > 0$ , there is a $\delta > 0$ such that $B_d(x; \delta) \subset B_{d'}(x; \epsilon)$ . I want to show that ${\cal T}' \subset {\cal T}$ .

Let U be open in ${\cal T}'$ . I want to show that it's open in ${\cal T}$ . Let $x \in U$ . Since the $d'$ -balls form a basis for ${\cal T}'$ , there is an $\epsilon > 0$ such that

$$x \in B_{d'}(x; \epsilon) \subset U.$$

By assumption, there is a $\delta > 0$ such that

$$x \in B_d(x; \delta) \subset B_{d'}(x; \epsilon).$$

Therefore, $x \in B_d(x; \delta) \subset U$ .

Now $B_d(x; \delta)$ is a ${\cal T}$ -open set containing x and contained in U. Since $x \in U$ was arbitrary, U is open in ${\cal T}$ . Therefore, ${\cal T}' \subset {\cal T}$ .

The standard metric on $\real^n$ is unbounded, in the sense that you can find pairs of points which are arbitrarily far apart. However, you can always replace a metric with a bounded metric which gives the same topology.

Definition. If $(X, d)$ is a metric space and $Y \subset X$ , then Y is bounded if there is an $M \in \real$ such that

$$d(x,y) \le M \quad\hbox{for all}\quad x, y \in Y.$$

Lemma. Let X be a metric space with metric d. Define

$$\overline{d}(x,y) = \min(d(x,y), 1).$$

(a) $\overline{d}$ is a metric.

(b) d and $\overline{d}$ induce the same topology on X.

Proof. (a) Let $x, y \in X$ . Since $d(x,y) \ge 0$ , $\overline{d}(x,y) = \min(d(x,y),1) \ge 0$ , and

$$\overline{d}(x,x) = \min(d(x,x), 1) = \min(0,1) = 0.$$

If $\overline{d}(x,y) = \min(d(x,y), 1) = 0$ , then $d(x,y) = 0$ , so $x = y$ . This shows that the first metric axiom holds.

Since $\overline{d}(x,y) = \min(d(x,y), 1) = \min(d(y,x), 1) = \overline{d}(y,x)$ , the second metric axiom holds.

To verify the third axiom, take $x, y, z \in X$ . Begin by noting that if either $d(x,y) \ge 1$ or $d(y,z) \ge 1$ , then $\overline{d}(x,y) = 1$ or $\overline{d}(y,z) = 1$ . Therefore,

$$\overline{d}(x,y) + \overline{d}(y,z) \ge 1 \ge \overline{d}(x,z).$$

Assume that $d(x,y) < 1$ and $d(y,z) < 1$ . Then

$$\overline{d}(x,y) + \overline{d}(y,z) = d(x,y) + d(y,z) \ge d(x,z) \ge \overline{d}(x,z).$$

This verifies the third axiom, so $\overline{d}$ is a metric.

(b) Observe that for $0 < \epsilon < 1$ , $B_d(x; \epsilon) = B_{\overline{d}}(x; \epsilon)$ . The idea is to apply the Comparison Lemma, shrinking balls if necessary to make their radii less than 1.

Let $x \in X$ and let $\epsilon > 0$ .

If $\epsilon < 1$ , then $x \in B_d(x; \epsilon) = B_{\overline{d}}(x; \epsilon)$ .

If $\epsilon \ge 1$ , then

$$x \in B_d(x; 0.5) = B_{\overline{d'}}(x; 0.5) \subset B_{\overline{d}}(x; \epsilon).$$

Therefore, the d-topology is finer than the $d'$ -topology. The other inclusion follows by simply swapping the d's and $d'$ 's.

It follows that boundedness is not a topological notion, since every subset is bounded in the standard bounded metric.

Example. The square metric on $\real^n$ is given by

$$\rho(x,y) = \max(|x_1 - y_1|, \ldots, |x_n - y_n|).$$

Relative to this metric, $B(x; \epsilon)$ is an n-cube centered at x with sides of length $2\epsilon$ .

First, I'll show that $\rho$ is a metric. Let $x = (x_1, \ldots, x_n), y = (y_1, \ldots, y_n) \in \real^n$ .

Clearly, $\rho(x,y) \ge 0$ and $\rho(x,x) = 0$ . If $\rho(x,y) = 0$ , then $|x_i - y_i| = 0$ for all i, so $x = y$ .

It's also obvious that $\rho(x,y) = \rho(y,x)$ .

If $x, y, z \in \real^n$ , then for each j,

$$\rho(x,y) + \rho(y,z) = \max_i \{|x_i - y_i|\} + \max_i \{|y_i - z_i|\} \ge |x_j - y_j| + |y_j - z_j| \ge |x_j - z_j|.$$

Therefore,

$$\rho(x,y) + \rho(y,z) \ge \max_j \{|x_j - z_j|\} = \rho(x,z).$$

Thus, $\rho$ is a metric.

Lemma. $\rho$ induces the same topology on $\real^n$ as the standard metric.

Proof. The idea of the proof is depicted below.

$$\hbox{\epsfysize=1.25in \epsffile{metric1.eps}}$$

Note that

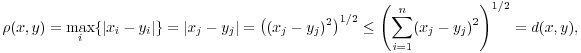
$$\rho(x,y) = \max_i \{|x_i - y_i|\} = |x_j - y_j| = \left((x_j - y_j)^2\right)^{1/2} \le \left(\sum_{i=1}^n (x_j - y_j)^2\right)^{1/2} = d(x,y),$$

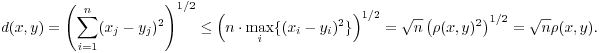
$$d(x,y) = \left(\sum_{i=1}^n (x_j - y_j)^2\right)^{1/2} \le \left(n\cdot \max_i \{(x_i - y_i)^2\}\right)^{1/2} = \sqrt{n} \left(\rho(x,y)^2\right)^{1/2} = \sqrt{n} \rho(x,y).$$

These inequalities may be used to get $\rho$ -balls contained in d-balls and d-balls contained in $\rho$ -balls; by the Comparison Lemma, this shows that the topologies are the same.

Lemma. The square metric induces the product topology on $\real^n$ .

Proof. If $x = (x_1, \ldots, x_n) \in \real^n$ , then

$$B(x; \epsilon) = (x_1 - \epsilon, x_1 + \epsilon) \times (x_2 - \epsilon, x_1 + \epsilon) \times \cdots \times (x_n - \epsilon, x_n + \epsilon).$$

The set on the right is open in the product topology. Since the square metric-basic sets are open in the product topology, any square metric-open set is open in the product topology.

Conversely, let

$$U = (a_1, b_1) \times (a_2, b_2) \times \ldots \times (a_n, b_n).$$

It is easy to check that sets of this form comprise a basis for the product topology.

Let $x = (x_1, \ldots, x_n) \in U$ , so $a_i < x_i < b_i$ for all i. Define

$$\epsilon = \min_i \{x_i - a_i, b_i - x_i\}.$$

Then

$$(x_i - \epsilon, x_i + \epsilon) \subset (a_i, b_i) \quad\hbox{for all}\quad i.$$

So

$$B(x; \epsilon) = \prod_i (x_i - \epsilon, x_i + \epsilon) \subset \prod_i (a_i, b_i) = U.$$

It follows that U is open in the square metric topology. Since the product topology basic sets are open in the square metric topology, any product topology open set is open in the square metric topology.

Lemma. Metric topologies are Hausdorff.

Proof. Let $(X, d)$ be a metric space, and let x and y be distinct points of X. Let $\epsilon = d(x,y)$ . Then $B\left(x; \dfrac{\epsilon}{2}\right)$ and $B\left(y; \dfrac{\epsilon}{2}\right)$ are disjoint open sets in the metric topology which contain x and y, respectively.

Lemma. If $(X,d)$ , $(Y,d')$ are metric spaces, the $\epsilon-\delta$ definition of continuity is valid. That is, a map $f: X \to Y$ is continuous at $x \in X$ if and only if for every $\epsilon > 0$ , there is a $\delta > 0$ such that if $\delta > d(x,y)$ implies that $\epsilon > d'(f(x), f(y))$ .

Proof. First, suppose that $f: X \to Y$ is continuous at $x \in X$ . Let $\epsilon > 0$ , and consider the ball $B(f(x); \epsilon)$ . Since this is an open set containing $f(x)$ , continuity implies that there is a $\delta > 0$ such that

$$f\left(B(x; \delta)\right) \subset B(f(x); \epsilon).$$

Now consider the conclusion to be established. Suppose $y \in X$ satisfies $\delta > d(x,y)$ . Then $y \in B(x; \delta)$ , so $f(y) \in f\left(B(x; \delta)\right)$ . Therefore, $f(y) \in B(f(x); \epsilon)$ , so $\epsilon > d'(f(x), f(y))$ .

Conversely, suppose that for every $\epsilon > 0$ , there is a $\delta > 0$ such that if $\delta > d(x,y)$ implies that $\epsilon > d'(f(x), f(y))$ . I want to show that f is continuous.

Let $x \in X$ , and let V be an open set in Y containing $f(x)$ . I want to find a neighborhood U of x such that $f(U) \subset V$ .

Since the $\epsilon$ -balls form a basis for the metric topology, I may find an $\epsilon > 0$ such that $f(x) \in B(f(x), \epsilon \subset V$ . By assumption, there is a $\delta > 0$ such that if $\delta > d(x,y)$ implies that $\epsilon > d'(f(x), f(y))$ .

Now consider the ball $B(x; \delta)$ . This is an open set containing x. If $y \in B(x; \delta)$ , then $\delta > d(x,y) > 0$ . Therefore, $\epsilon > d'(f(x), f(y))$ , so $f(y) \in B(f(x); \epsilon)$ . This shows that $f(B(x; \delta)) \subset B(f(x); \epsilon) \subset V$ , so f is continuous.

Definition. If X is a set, a sequence in X is a function $x: \integer^+ \to X$ .

It's customary to write $x_n$ for $x(n)$ in this situation, and to abuse terminology by referring to the collection $\{x_n\}$ as "the sequence".

Definition. Let X be a topological space. A sequence $\{x_n\}$ converges to a point $x \in X$ if for every neighborhood U of x, there is an integer N such that $x_n \in U$ for all $n \ge N$ .

$x_n \to x$ means that $\{x_n\}$ converges to x.

Lemma. Let X be a Hausdorff space. Convergent sequences converge to unique points.

Proof. Let $x_n \to x$ and $x_n \to y$ . I want to show that $x = y$ .

Suppose $x \ne y$ . Since X is Hausdorff, I can find disjoint neighborhoods U of x and V of y. Since $x_n \to x$ , I can find an integer M such that $n \ge M$ implies $x_n \in U$ . Since $x_n \to y$ , I can find an integer N such that $n \ge N$ implies $x_n \in V$ . Therefore, for $n \ge \max(M,N)$ , I have $x_n \in U \cap V = \emptyset$ . This is nonsense, so $x = y$ .

In particular, limits of sequences are unique in metric spaces.

Lemma. ( The Sequence Lemma) Let X be a topological space, let $Y \subset X$ , and let $x \in X$ . If there is a sequence $\{x_n\}$ with $x_n \in Y$ for all n and $x_n \to x$ , then $x \in \cl{Y}$ . The converse is true if X is a metric space.

Proof. Suppose that there is a sequence $\{x_n\}$ with $x_n \in Y$ for all n and $x_n \to x$ . Let U be a neighborhood of x. Find an integer N such that $x_n \in U$ for all $n \ge N$ . Obviously, U meets Y. This proves that $x \in \cl{Y}$ .

Conversely, suppose that X is a metric space and $x \in \cl{Y}$ . For each $n \in \integer^+$ , the ball $B\left(x; \dfrac{1}{n}\right)$ meets Y, so I may choose $x_n \in B\left(x; \dfrac{1}{n}\right) \cap Y$ . I claim that $x_n \to x$ .

Let U be a neighborhood of x. Since the open balls form a basis for the metric topology, I may find $\epsilon > 0$ such that $B(x; \epsilon) \subset U$ ; then I may find $N \in \integer^+$ such that $\dfrac{1}{n} < \epsilon$ , so $B\left(x; \dfrac{1}{N}\right) \subset B(x; \epsilon)$ .

For all $n \ge N$ , I have $\dfrac{1}{n} < \dfrac{1}{N}$ , so $x_n \in B\left(x; \dfrac{1}{N}\right)$ . Since $B\left(x; \dfrac{1}{N}\right) \subset U$ , I have $x_n \in U$ for all $n \ge N$ .

This proves that $x_n \to x$ .

Theorem. Let X be a metric space, let Y be a topological space, and let $f: X \to Y$ . f is continuous if and only if $x_n \to x$ in X implies that $f(x_n) \to f(x)$ in Y.

More succinctly, continuous functions carry convergent sequences to convergent sequences.

Proof. Suppose f is continuous, and suppose $x_n \to x$ in X. Let V be a neighborhood of $f(x)$ in Y. By continuity, there is a neighborhood U of x such that $f(U) \subset V$ .

Since $x_n \to x$ , there is an integer N such that $x_n \in U$ for all $n \ge N$ . Then $f(x_n) \in f(U) \subset V$ for all $n \ge N$ . This proves that $f(x_n) \to f(x)$ .

Conversely, suppose that $x_n \to x$ in X implies that $f(x_n) \to f(x)$ in Y. To show f is continuous, it will suffice to show that for all $A \subset X$ , I have $f(\cl{A}) \subset \cl{f(A)}$ .

Thus, take $x \in cl{A}$ . I want to show that $f(x) \in \cl{f(A)}$ .

Now X is a metric space and $x \in cl{A}$ , so by the Sequence Lemma, there is a sequence of points $\{x_n\} \subset A$ with $x_n \to x$ . By hypothesis, this implies that $f(x_n) \to f(x)$ . Since $\{f(x_n)\}$ is a sequence in $f(A)$ , the Sequence Lemma implies that $f(x) \in \cl{f(A)}$ . Therefore, f is continuous.

Definition. Let $\{f_n: X \to Y\}$ be a sequence of functions from X to Y, where Y is a metric space. $\{f_n\}$ converges uniformly to a function $f: X \to Y$ if for every $\epsilon > 0$ , there is an integer N such that

$$d(f_n(x), f(x)) < \epsilon \quad\hbox{for}\quad n \ge N \quad\hbox{and}\quad x \in X.$$

Theorem. Let $\{f_n: X \to Y\}$ be a sequence of continuous functions from X to Y, where Y is a metric space. If $\{f_n\}$ converges uniformly to $f: X \to Y$ , then f is continuous.

This is often expressed by saying that a uniform limit of continuous functions is continuous.

Proof. Let $f(a) \in Y$ and let $B(f(a); \epsilon)$ be a neighborhood of $f(a)$ . I want to find a neighborhood U of a such that $f(U) \subset B(f(a); \epsilon)$ .

First, uniform continuity implies that there is an integer N such that

$$d(f_n(x), f(x)) < \dfrac{\epsilon}{3} \quad\hbox{for}\quad n \ge N, \quad x \in X. \eqno{\rm (*)}$$

In particular,

$$d(f_N(a), f(a)) < \dfrac{\epsilon}{3}.$$

$f_N$ is continuous, so there is a neighborhood U of a such that $f_N(U) \subset B\left(f_N(a), \dfrac{\epsilon}{3}\right)$ . Thus,

$$d\left(f_N(x), f_N(a)\right) < \dfrac{\epsilon}{3} \quad\hbox{for all}\quad x \in U.$$

Moreover, restricting (*) to $n = N$ and $x \in U$ , I have

$$d(f_N(x), f(x)) < \dfrac{\epsilon}{3} \quad\hbox{for all}\quad x \in U.$$

Therefore, the triangle inequality implies that

$$d(f(x), f(a)) \le d(f_N(x), f(x)) + d\left(f_N(x), f_N(a)\right) + d(f_N(a), f(a)) < \dfrac{\epsilon}{3} + \dfrac{\epsilon}{3} + \dfrac{\epsilon}{3} = \epsilon$$

for all $x \in U$ .

This proves that f is continuous.

Example. For $n \in \integer^+$ , let $f_n: \real \to \real$ be defined by

$$f_n(x) = \dfrac{x}{nx + 1}.$$

For fixed x, $\displaystyle \lim_{n\to \infty} \dfrac{x}{nx + 1} = 0$ . Thus, this sequence of functions converges pointwise to the constant function 0.

The picture below shows the graphs of $f_n$ for $n = 1, 2, 3, 4, 5$ on the interval $0 \le x \le 1$ .

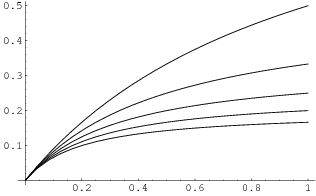
$$\hbox{\epsfysize=1.75in \epsffile{metric2.eps}}$$

I will show that the convergence is uniform on the interval $0 \le x \le 1$ . Thus, choose $\epsilon > 0$ ; I must find an integer N such that if $n \ge N$ , then

$$|f_n(x)| < \epsilon.$$

Since $f_n'(x) = \dfrac{1}{(nx + 1)^2}$ , $f_n$ is an increasing function; $f_n(1) = \dfrac{1}{n + 1}$ , so it follows that

$$|f_n(x)| < \dfrac{1}{n + 1} \quad\hbox{for}\quad 0 \le x \le 1.$$

Now choose N such that $\dfrac{1}{N + 1} < \epsilon$ . Then if $n \ge N$ ,

$$|f_n(x)| < \dfrac{1}{n + 1} \le \dfrac{1}{N + 1} < \epsilon.$$

This proves that $f_n$ converges uniformly to 0 on $0 \le x \le 1$ .

Example. For $n \in \integer^+$ , let $f_n: \real \to \real$ be defined by

$$f_n(x) = \dfrac{1}{nx + 1}.$$

For fixed $x \ne 0$ , $\displaystyle \lim_{n\to \infty} \dfrac{1}{nx + 1} = 0$ . Thus, this sequence of functions converges pointwise to the constant function 0 for $x \ne 0$ . It converges pointwise to 1 for $x = 0$ .

The picture below shows the graphs of $f_n$ for $n = 1, 2, 3, 4, 5$ on the interval $0 \le x \le 1$ .

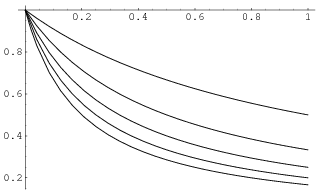
$$\hbox{\epsfysize=1.75in \epsffile{metric3.eps}}$$

I will show that the convergence is not uniform on the interval $0 < x < 1$ . In fact, I will show that there is no integer N such that if $n \ge N$ , then

$$|f_n(x)| < \dfrac{1}{4}.$$

To see this, it suffices to note that $f_n\left(\dfrac{1}{n}\right) = \dfrac{1}{2}$ , so there will always be a point in $0 < x < 1$ where the function exceeds $\dfrac{1}{4}$ .

Therefore, $\{f_n\}$ converges pointwise, but not uniformly, to the zero function.

Send comments about this page to: bikenaga@marauder.millersville.edu.

Last updated:

Bruce Ikenaga's Home Page

Math Department Home Page

Millersville University Home Page

Copyright 2009 by Bruce Ikenaga