ArcGIS Coordinate Systems
Unprojected Maps
There is an insidious disease which has infected the Internet. It is caused by uneducated or lazy map makers (they cannot be called cartographers). It is . . . the Unprojected Map!
Unprojected maps are maps in which the non-Euclidean Earth coordinates, recorded in degrees, minutes and seconds or decimal degrees, are used without mathematical conversion as coordinates on a flat plane in which one degree of latitude is the same length as one degree of longitude. Technically, there is a map projection called the Plate Carrée projection which has the characteristics and appearance of the unprojected map, but the Plate Carrée projection has very specific preferred applications, such as when depicting a very small urban area or a relatively small area along the equator. It is clear that most unprojected maps are not intentionally emulating those properties.
Three examples of unprojected maps are presented here. It is not necessarily easy to tell whether a map is unprojected or not, but it will be easy if the map covers a well-known area that you are used to seeing on globes or on projected maps.
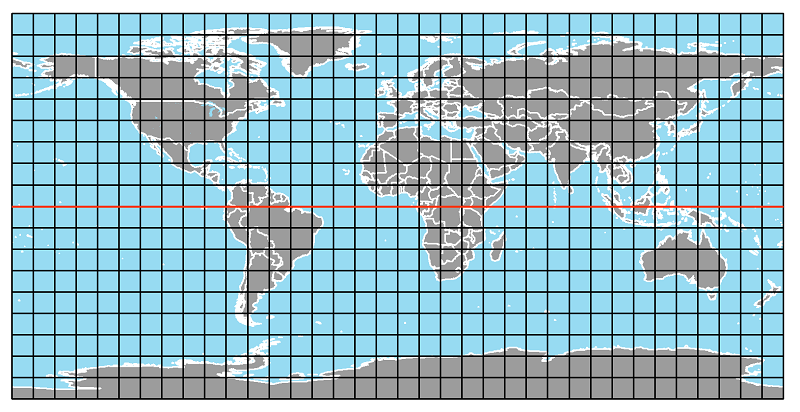
The Unprojected World Map:
There are cylindrical projections, as you will see, which come close to the distortion visible here. The key difference, though, is that the distortion on projected maps either serves a purpose itself, or is unavoidable because of another Earth/globe property that must be preserved. The unprojected world map has no redeeming property or purpose.
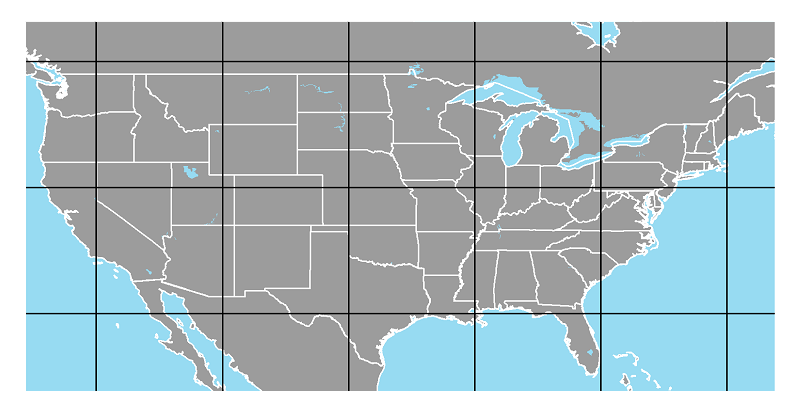
The Unprojected US Map:
These unprojected maps really stand out because virtually every map showing the entire US is in the family of Conic projections. The stretched-out (east-to-west) appearance and the straightened boundary with Canada are the most obvious clues.
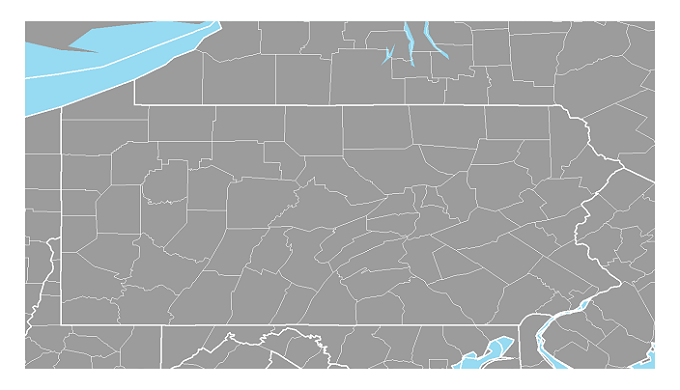
The Unprojected Pennsylvania Map:
Maps showing the entire state of Pennsylvania are usually projected on a Conic projection grid also. It is difficult to pinpoint any particular shape changes to the state boundary, but once again the stretched-out appearance is the best clue.
GIS Data Coordinates
There is a difference between the coordinates a GIS layer is stored in and the coordinates that layer is displayed in. The former are called the data coordinates or "geographic coordinates" and the latter are called the "projected coordinates." One of the computer files that makes up a shapefile (the one ending in .SHP) is the data file containing the coordinates of each point that either makes up a point feature itself or serves as a pivot point along a line feature or along the outline of an area feature. Those "geographic" coordinates have to be recorded in some unit of measure, such as in decimal degrees, or in the feet or meters measurements of a projected coordinate system such as UTM or state plane coordinates. Those geographic coordinates must be translated to positions on your computer screen, which has its own plane geometry coordinate system with different units of measure; obviously, those coordinates change every time you move or zoom the map, in addition to every time you make general changes like choosing a different map projection. The screen's coordinates make up the "projected coordinates." The projected coordinates also apply to the paper on which the GIS map gets printed.
The projected coordinates must have a map projection applied to control the distortion caused by representing the round Earth on a flat surface. Once projected, the resulting map could have a grid displayed that shows the projected graticule with coordinates in realistic units of measure. For example, if a cartographer created a world map to be printed and decided to project it as a rectangular cylindrical projection, the projected points' locations would be calculated in decimal fractions of an inch to be positioned on a piece of paper. The cartographer could then label the paper map's graticule with the more realistic degrees of latitude and longitude of the Earth’s surface.
However, the map could also be labeled with different real-world units of measure, such as feet or meters measured from a fixed point on that map. If those units of measure had been used to store the geographic coordinates in the first place, the projection process becomes a lot easier for the cartographer and for the computer. That was the rationale behind devising the UTM and State Plane coordinate systems. The geographic coordinates for the UTM coordinate system are stored in metric units, based on an original projection process that displayed the map area in print using Mercator’s projection laid “transversely”. Similarly, if a US state map (or a map of part of a state) was projected using a conic projection, a grid was set up with a starting point (0,0) from which every location on the map could be measured in feet, and then all locations were stored in those feet coordinates, the result would be geographic coordinates in the State Plane Coordinate System for that state (or that part of the state).
Projections in GIS
GIS software uses map projections in two ways:
- Control the map grid in order to portray the round earth on a flat surface (paper or computer screen).
- Combine on one map a data theme stored in one coordinate system with a different data theme stored in another coordinate system (not all GIS programs can handle this scenario).
One of the key features of GIS software is its ability to project any map or map layer. Since projecting a map layer means converting the actual Earth coordinates of its map features to paper or screen coordinates, it is really just the application of a mathematical equation.
The beauty of GIS is that most of the time the software knows (from one of the shapefile's computer files) what geographic coordinates (including units of measure) the layer was saved in. In fact, it determines from that information a default map projection (or projected coordinate system) with which to display the map. For example, in ArcMap, the geographic coordinates of the first layer added to a new map are used as simple X,Y coordinates that are just translated to the dimensions of the computer screen: a simple projected coordinate system. If the geographic coordinates were decimal degrees, the result would be an unprojected map (see above), and would look rather distorted. If a second map layer with state plane feet for its geographic coordinates is added, ArcMap converts its geographic coordinates to that default unprojected coordinate system "on the fly." However, you can override that default map projection and decide on a different one. That is the starting point for the discussion below.
But we already saw that a map layer can also be stored in already-projected coordinates, such as UTM meters or State Plane feet. If that is the first layer added to a map, that map will not look distorted when it is initially displayed; it is already projected. again, adding additional layers will project them to that projection on the fly. If you want the map to have a different projection than the initial one the first layer was stored in, the mapping software must "unproject" it back into decimal degrees (it does this without the user's involvement) and then apply the new projection. Related to this on-the-fly map projection capability of GIS programs is the ability to convert a layer's geographic coordinates permanently from one coordinate system to another.
A map whose layers are all stored in decimal degrees must be projected, or it will look distorted like the maps above. An exception is if the map area is relatively small and right on the equator, where one degree of latitude is the same distance as one degree of longitude. Projecting it, though, is just a process of selecting a new projection from the choices built into the software (see below).
Projections in Google Maps
The geographers who helped Google get Google Maps started had to decide on a map projection for displaying their maps. The biggest challenge was that it had to look reasonable whether the user was zoomed in to a small local area or zoomed all the way out to look at the whole country or world. As a matter of fact, if you look closely as you zoom in or out in Google Maps, there is a small range of zooming in which the map is getting bigger or smaller, but if you zoom to an extent beyond that small range you are actually looking at a new map. To make that process look as seamless as possible, Google adopted one map projection for all their maps. It is actually a modified Mercator projection called the "Web Mercator Auxiliary" projection. When Esri started producing their own online map display tools, they followed Google's lead and use that same projection. The only exception is that when you zoom out far enough that the Mercator projection's limitations become obvious it will switch to a planar projection, one that can be manipulated like a spinning globe.
Projections in ArcGIS
Projecting Maps
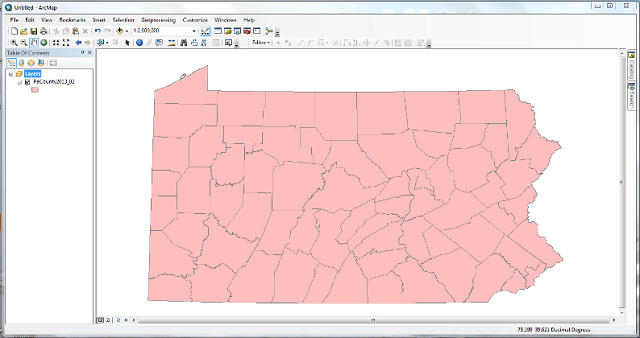
Let's follow an example in which you want to project the unprojected map of Pennsylvania below. In order to apply a map projection to an unprojected map, or to a map whose initial or current projection is different than what you want, here is a brief list of the steps.
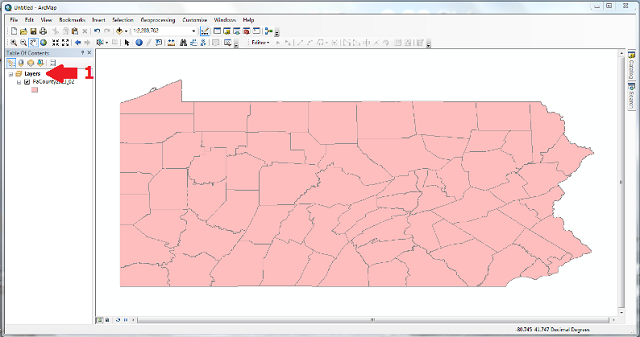
- Right-click on the word "Layers" at the top of the Table of Contents area of the ArcMap window.
- Select "Properties" at the bottom of the list of links that opens.
- Select the "Coordinate System" tab in the new "Data Frame Properties" window that opens.
- The resulting window operates like a file browser with folders and subfolders (because each map projection definition is a separate file stored in a system of folders). At the highest folder level, select the "Projected Coordinate Systems" folder.
- For the Pennsylvania map, first select the "State Plane" folder, and within that, select the "NAD 1983 (US Feet)" folder.
- Within that folder, select the specific projection named "NAD 1983 StatePlane Pennsylvania South FIPS 3702 (US Feet)," and click "OK."
The ArcMap Coordinate System Dialog
The first big thing to understand, in order to grasp the logic of how map projections are used in ArcGIS, is that they are not referred to as "map projections," but as "projected coordinate systems." As described earlier, the process begins with knowing the geographic coordinates of the first map layer added to the current map, so that you can identify the default projection (or lack of projection) of the map. Whatever that first layer's geographic coordinates are, all subsequently added layers will be projected (if necessary) to that coordinate system. When you open the map's (not the layer's) Properties dialog and click on the Coordinate System tab, the initial selection will be that default geographic coordinate system.
The Coordinate System dialog is basically a file explorer with two folders. The first folder lists the "Geographic Coordinate Systems" arranged into several subfolders. There are actually quite a lot of different choices given there, with the variety deriving from all of the different regions of the world (with their equivalents to the US's state plane coordinates) as well as many very specialized choices. There are analytical applications for these that go well beyond the scope of this course, and Esri prides itself on being comprehensive with the options. The second Coordinate System dialog folder lists the "Projected Coordinate Systems" arranged into quite a few different subfolders.
ArcMap only allows there to be one "coordinate system" to be defined at a time for the map, and that coordinate system is the one with which the map is displayed. Therefore, to project the map we replace the default "geographic" coordinate system with a "projected" coordinate system. To do that, collapse the folder of Geographic Coordinate Systems, and expand the folder of Projected Coordinate Systems.
It would be nice for our purposes if the subfolders in the folder of Projected Coordinate Systems had names like Planar, Conic and Cylindrical, but they don’t. The logic in ArcMap works like this: assuming that many ArcGIS users are not professional geographers, they organized the folders along the lines of what criteria would be most obvious in choosing projections. The primary criteria have to do with where in the world the map area is. The options are the names of their main subfolders: Continental, State Plane, World, etc. The best guess I can make about why they chose the subfolder names they did was to distribute the individual projections as logically but also as evenly as they could (so each folder had many options). Those subfolders generally have sub-subfolders that contain the actual choices of projected coordinate systems. In this dialog, the folders, subfolders and sub-subfolders are not just an analogy; each coordinate system—geographic and projected—is represented by a separate file stored in that folder structure.
There are literally hundreds of choices of projected coordinate systems in ArcMap.
The Finished Map
Once the map is projected, the remaining tasks are aimed at completing the map. Depending on the purpose of the map (see the discussion early in the course about the basic mapping procedure), information can be represented in a number of ways; we learned some of the ideas of topographic map symbology earlier in the course, and will learn about the types of thematic maps later in this section.
For now, adding other map layers can enhance the effectiveness of the map. For the projected map below, my next step would be to add highways and rivers. When they are added, because the map window has already been projected, they will appear to be already projected, too.
Choosing an Appropriate Projection
Appropriate Map Projection Choices
The best map projection choice will always depend very much on the map's purpose and spatial context. The list below should be considered to be illustrative, and not comprehensive. There are literally hundreds of different map projections that have been developed since the original Mercator Projection; most are easily enough programmed. However, the number of different projections you will ever use is probably very small, probably fewer than a dozen.
ArcGIS offers abundant choices in its organizational structures. As you saw on the previous page, the map projection is chosen from a menu of many projections, which are divided them into several levels of categories. Even for basic needs, such as World maps, US maps or Pennsylvania maps, the number of choices can be intimidating. You will also notice that, in addition to the projection name, a 4-5 digit identification number is given, which is part of an internationally-recognized system. If you visit multiple projection categories in ArcGIS, you will see that many map projections are designed for very specific areas of the world or US.
Consider that in most job situations your company or organization or agency will probably have a certain region or territory of operation. The maps you might produce for their work will generally focus on that area. It is not very likely that you will produce world maps and US maps and state maps and local maps. The list below has been kept simple for that reason. If your scope of work focuses on one of those areas, you may well have to go beyond this list within that area.
| Area | Purpose: Sizes of areas is primary. "Equal-Area" | Purpose: Shapes of areas is primary. "Conformal" |
|---|---|---|
| World | All are non-rectangular projections. Mollweide and Sinusoidal Projections are classics, joined by the Robinson and Winkel-Tripel Projections. | Mercator is the classic, but significantly distorts polar areas. For a non-rectangular projection, Robinson and Winkel-Tripel are compromise projections. |
| USA | Albers Equal Area Conic Projection. | Lambert's Conformal Conic Projection. |
| Pennsylvania | Albers Equal Area Conic Projection. | Lambert's Conformal Conic Projection. This is the basis for the Pennsylvania State Plane coordinate system (see last unit). |