The Quantitative Difference

We have already seen how ordinal (classified) symbols can be used to represent data values using size and color symbology options. In this unit we are using similar symbols with the same appearance options in a different way to represent data. The difference is that, whereas a classified (ordinal-level) thematic map creates a limited number of different symbols to reflect the entire range of data values for a set of map features, unclassified and proportional thematic maps approximate reality by representing each map feature's unique data value by a correspondingly unique symbol for that feature.

Keep referencing the Thematic Map Types chart from several units ago. The quantitative-level thematic maps have more specific map types than the other levels of measurement, especially for area features. Two of those map types, graduated symbols (this occurs at the ordinal level of measurement as well) and isolines, are repeated for two different types of geographical features, both points and areas. Perhaps the biggest challenge in learning about the quantitative-level thematic maps is keeping the different data requirements and symbology options straight.

Of course, we will also be examining how these maps are created in ArcMap. In a couple of cases the best we can do here is to view completed maps; ArcMap is not able to produce them without extra software or extra data or graphical manipulation. As before, we will also have to face some of ArcMap's terminology differences with the language of cartographers. For example, we have already seen that ArcMap calls choropleth maps "graduated color" maps and treats flow maps as a version of a graduated symbols map (we will continue that interpretation here by considering flow maps here with the graduate symbols representation).

Proportional Graduated Symbols Maps

Data Requirements for Graduated Symbols Maps

We start our discussion here with the quantitative version of the graduated symbols map. As stated in the description of the ordinal graduated symbols map, the data requirements for area map features are that the variable must be a “count” quantity and not a ratio or density or other calculation. The reason for this is that the symbol size visually compared to the size of the area it represents work as a visual representation of density. If the graduated symbol is a circle, then the circle radius will be directly proportional to the data value it represents; in other words, there is no classification step. For any shape used as an alternative symbol, some dimension of the shape (height, width, length, etc.) will be used in the same way: each separate symbol will be sized in direct proportion to the data value it represents.

As you see in the Thematic Map Types chart, graduated symbols maps, both classified and proportional, can be used for point features and area features. On that chart proportional graduated symbols used with point features requires that those point features represent "discrete phenomena" in contrast to "continuous phenomena." The distinction is that the point locations should represent something that stands alone at that place, such a city surrounded by countryside or a water well surrounded by land with no wells (until at some location there happens to be another well). With that distinction made, the symbol size will best represent the relative size of the data value. We are less concerned about whether the data represented are counts vs. calculated values (ratios, densities, etc.) because we are more focused on the magnitude of each individual feature than the density of multiple features in an area.

Since flow lines are considered graduated symbols in ArcMap, we have to understand whether their data requirements are more like the counts of the graduated symbols for area features or the discrete values of the graduated symbols for point features. Flow maps are meant to show the quantities of some sort of material flowing along that route. In the case of roads or railroad tracks it will be vehicles or freight or passengers. In the case of pipelines it will be some measure of the amount of fluids. For wires there are various measures of the amount of information flowing. These quantities are more like the counts of area maps for showing graduated symbols. Represent the quantities, not the rates of flow or similar calculated measures. However, the quantities would still require some sort of time context. The number of vehicles traveling on a road can be measured by a counting hose stretched across the road. But that is not a permanent set up. The hose might be there for a few hours or a day. The values for all the roads in that GIS layer are adjusted proportionally as if they were measured for the same length of time.

Graduated Symbols Maps Show Quantities using Symbol Sizes

For point features, such as cities on a US map, the graduated symbol is centered on the actual city location, but with area features, like the US states, the symbol is centered within the outline of each feature. If some point locations are close together or some neighboring areas are small, the symbols become crowded together in some area(s) of the map. A little overlap between neighboring circles is fine, and is actually better than seeing a lot of white space between all circles, but too much overlap will make it harder to identify which circle goes with which map feature.

Controlling for those size issues requires you to set the symbol size in the Symbology dialog and then go back and look at the map. You can control the visual effect of that relationship by adjusting the scale of the map, though this should only be used to a limited degree. In ArcMap your control over symbol sizes for graduated symbols is limited, as you will see below, so the scale adjustment could become necessary.

One other consideration applies to maps with graduated symbols, especially with those symbols presented as circles. Start by considering square symbols. The first shape is considered 1 square unit in area: one unit wide by one unit tall. The second shape, then, is 2 square units in area and the third one is 4 square units. Even though the dimensions of the third shape are double those of the first square (2 units wide by 2 units tall), it is 4 times bigger. To make a square that is twice the area of the first square, its dimensions would have to be 1.4142 units x 1.4142 units (1.4142 is the square root of 2) in size, which are the dimensions of the last shape. Generally, the “proportional” relationship between the data value and the symbol size should relate to the symbol’s area, not any one dimension.

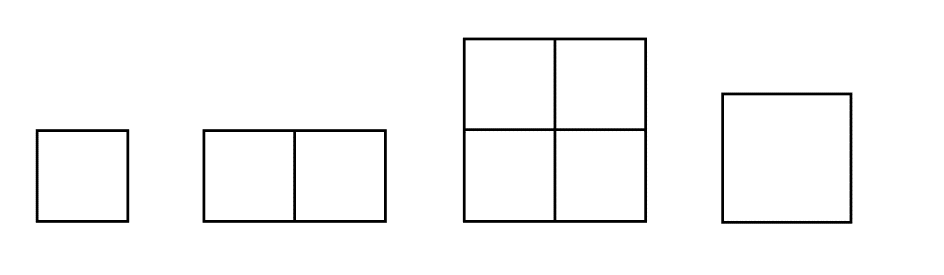
Something similar happens with circle symbols. To create a circle that is twice the area of another we cannot just double the diameter of the first circle. The formula for the area of a circle, πr², can be used to demonstrate that. Compare two circles, one with a radius of 3 and the other with a radius of 6. The area of the first circle is 28.27 and the area of the second circle is 113.10. Instead, 4.244 is the correct radius for a circle whose area is twice that of the first circle. However, a psychologist with the last name Flannery did some research on visual perception and showed that what people perceive to be a circle twice the area of another circle is actually a little more than twice the area of the first circle. This is referred to as the "Flannery compensation." ArcMap gives you the option to apply the Flannery compensation when you create a Proportional Symbols map, which you should always check. If you compare the same map with the Flannery compensation unselected first and then selected the second time, you will see that the effect of applying it is to make the larger circles bigger than they would be otherwise.

For the line thicknesses of a proportional flow map, think of them the same way as the proportional graduated symbols. As the data value gets bigger the line will get thicker. However, it is much more difficult to see subtle differences in line thicknesses, such as trying to decide whether one line is twice as thick as another. For that reason, it is best to use this kind of map only to show very obvious relationships.

Try It

First add the appropriate layers. In this case, the main data layer is the universities of the Pennsylvania State System of Higher Education. The ArcGIS topographic basemap and the layer of county boundaries are added to provide context.

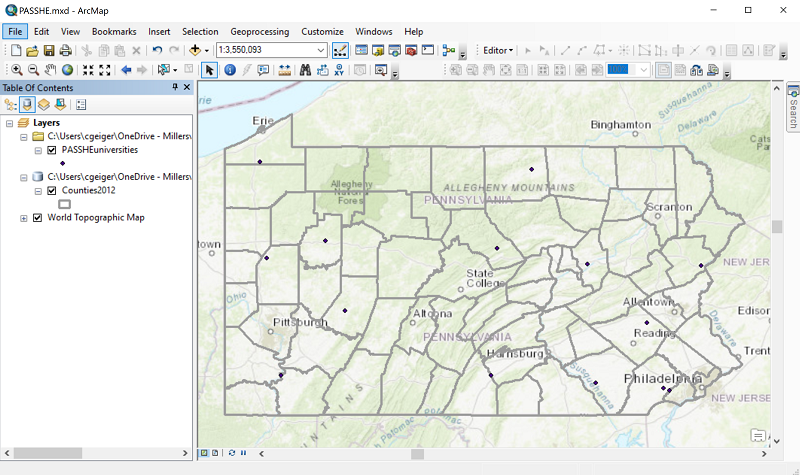
Next in ArcMap we define the main data layer's symbology. In this map we will size the graduated circles using data showing the number of students enrolled at each university in 2019. In the Symbology dialog the main decisions to make are:

1. The map type, on the left. A proportional graduated symbols map in ArcMap is simply a "Proportional symbols" map.
2. The name of the Value variable. Remember, this should be a count type of magnitude measurement. In this example, the variable name is "Enrolled19."



3. The "Min Value" button gives you the only controls you have over the symbology. Click on that button to open the standard ArcMap point symbols dialog. The default symbol is a circle with a different-colored edge to it. In the dialog, you can change the interior color of the circle, the edge color and the circle diameter of the smallest circle only. You can only control the minimum circle size because all other circles are calculated proportionally to that smallest circle. You will notice that I also applied some transparency to my circles.
4. Finally, you will see a checkbox labeled "Appearance Compensation (Flannery)." As discussed above, you should select this option. Note that it becomes unavailable if you make a selection in the "Unit" box below the variable selection, so that is not recommended.

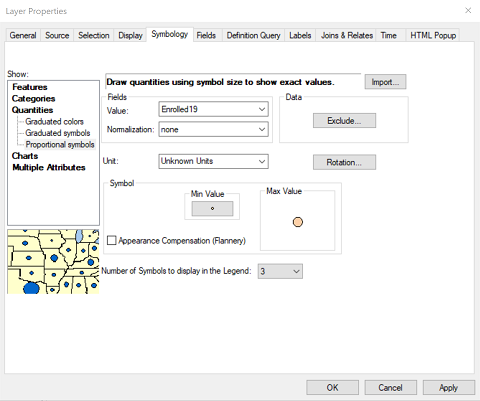
The resulting map shows the effects of these decisions, particularly the relative sizes of our state universities. It demonstrates some of the potential challenges of using graduated circles (ordinal or proportional), such as the effect of covering or letting through some of the underlying basemap and what happens when ArcMap has to draw two graduated circles that overlap. In the latter case, the circles are drawn largest to smallest so the small circles will always be visible.

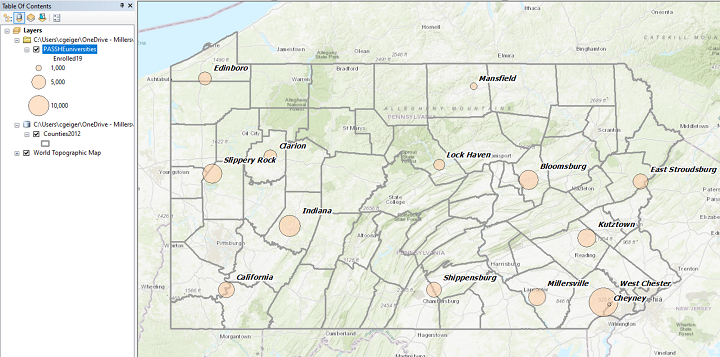
The transparency is achieved after the Symbology dialog is finished. In the Layer Properties window, the tab to the left of the Symbology tab is the Display tab. It contains the control for layer Transparency.

Notice the legend representation for the proportional version of the graduated symbols map. Three different circles sizes are shown, each labeled with a single rounded number. These circles are drawn to the same scale of the circles on the map, and will be represented in exactly the correct scale if you add a legend to the map in Layout view. This is the correct way to represent quantitative-level data. Ordinal-level thematic maps show all possible symbol sizes of the thematic layer labeled with the range of data values each represents, while that is impossible for a quantitative-level map. So, the quantitative-level map's legend for the main thematic layer shows sample small, medium and large symbols so the reader can estimate the value for symbols of sizes relative to them.

Dot Maps

Dot Maps Show Densities

Dot maps, or dot density maps, show data by varying the number of dots filling a set of areas. Dot maps are proportional data representations: each dot represents the same number of things on the map. That number is never "1" so that, for example, on a map of beer distributors across the state of Pennsylvania, each dot cannot represent one beer distributor, but can represent three. The difference is that if it represented one, then people viewing the map would expect the dots to be placed at the exact location of each distributor, but not if it represents three. The key GIS layer for this map would depict the counties of Pennsylvania and its attribute table would include one data column showing the number of beer distributors for each county as quantities that are "counts." There would not be enough information there to show exact locations. A map that does show each distributor at its exact location is a topographic map of the distributors (point features), not a thematic map of the counties (area features).

In the dot map below, each dot represents 10,000 acres of soybeans harvested in the US (US Dept. of Agriculture). The dots are displayed against a background of the counties of the US, which is most likely how the data were reported to the US Department of Agriculture. The dots are a little tricky to see in areas where they are relatively few, but the concentration of soybean farming in the central plains of the US is clearly shown. Notice also this map's arrangement of the inset maps for Alaska and Hawaii, which is being advocated by a number of cartographers for maps featuring US states.

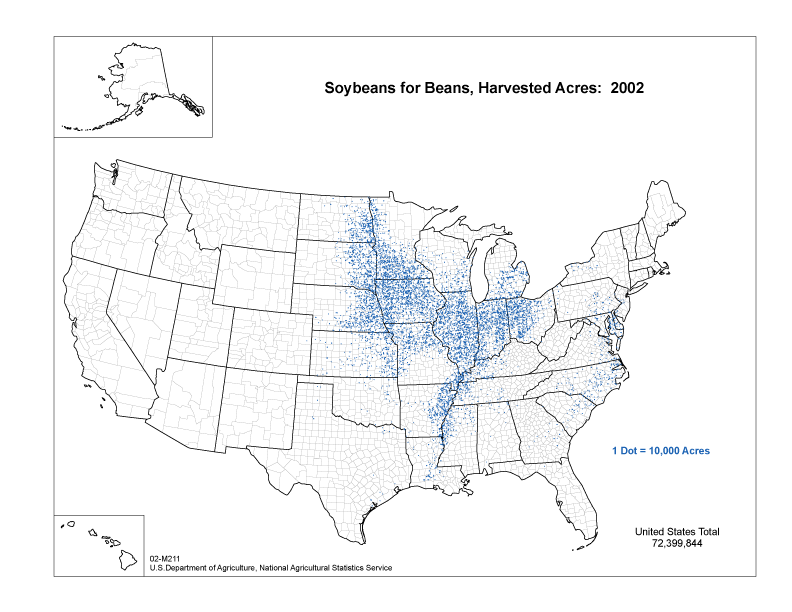
The legend of the map above is also important to examine. It is the simplest of all the thematic map legends we will encounter, but it tells you all you need to know. On this map the legend uses all words (and a number, of course) to state the value of each dot. There is no expectation that anyone will try to count the dots or calculate any subtotals, but that legend is enough to give a relative sense of how much more productive one are of the map is than another. Another version of the legend would show a dot followed by the number and its units of measure. The tricky thing for the example below is that the default legend that ArcMap makes for a dot map is more complicated and awkward than this one.

Data Processing for Dot Maps

The concept behind dot maps is that the varying densities of dots across the map reflects the density of the mapped feature just by virtue of the symbol representing a fixed number of those "things." You could achieve the same objective if you had data showing the exact location of each "thing," but very often that is not available, and you only have counts of those things for some level of area features. That aspect is very important, that even though the objective is to show relative densities, your data must represent counts within area features.

The dot map feature in ArcGIS places the appropriate number of dots randomly within the area features. You as the software user and cartographer do not control those random locations. ArcGIS does include more sophisticated procedures for “guiding” the dot locations, but that is beyond the scope of this course.

Try It

In this step-by-step example, you will be seeing the steps needed to turn a set of count data into a Dot Map. The ArcGIS procedure for this fits the descriptions above, but focus on the getting the sequence right because it can save work later. The data table records several types of information about preserved farms across the state of Pennsylvania, courtesy of the PA Department of Agriculture. The variable to be mapped is the number of preserved farms in each county.

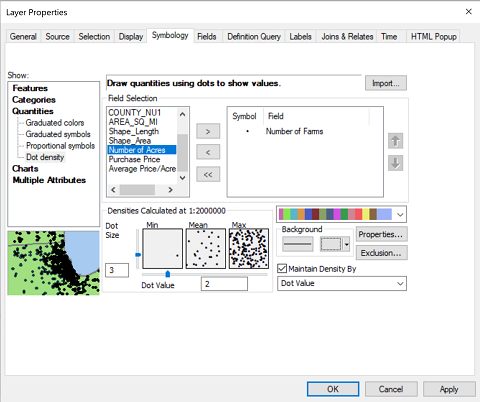
1. Adding the GIS layer in this case required joining the data table from the Department of Agriculture to a Pennsylvania counties layer. Not every county has preserved farms, explaining the word "" in this illustration.



2. The next few steps take place in the Symbology dialog box. First, select "Dot density" in the list of thematic map types on the left.



3. In the same dialog, the section to the right of the previous set has two boxes, one with a list of all the data fields and the other with a list of the fields that will be represented with dots. If you have additional layers in your map, they may already show up on the right. If there are any that should not be symbolized with dots, just select them and click on the "<" button between the two windows to remove them. If the correct field does not yet show up there, just select it in the left-hand box and click on the ">" button between the two windows to add it. The other function of this part of the dialog is to change the symbol size and color. Do so by clicking on the actual symbol shown there and make decisions in the usual ArcMap point symbol dialog.
4. There are three smaller boxes labeled "Min," "Mean" and "Max" below the two you were just working with. To adjust the dot value (in this case the number of farms represented by each dot) there is a box below those three where you can change that. After taking this screenshot image I changed the 2 to a 3. To the left is a similar spot where you can change the dot sizes.
5. The only other controls I recommend you use are the two below the word "Background" just to the right of the last ones you were just working with. The control on the left lets you control the appearance of the borders of the areas, and the control on the right lets you control the appearance of the background color. In my case I made the borders a thin black line and the background completely transparent. Here is the resulting map:



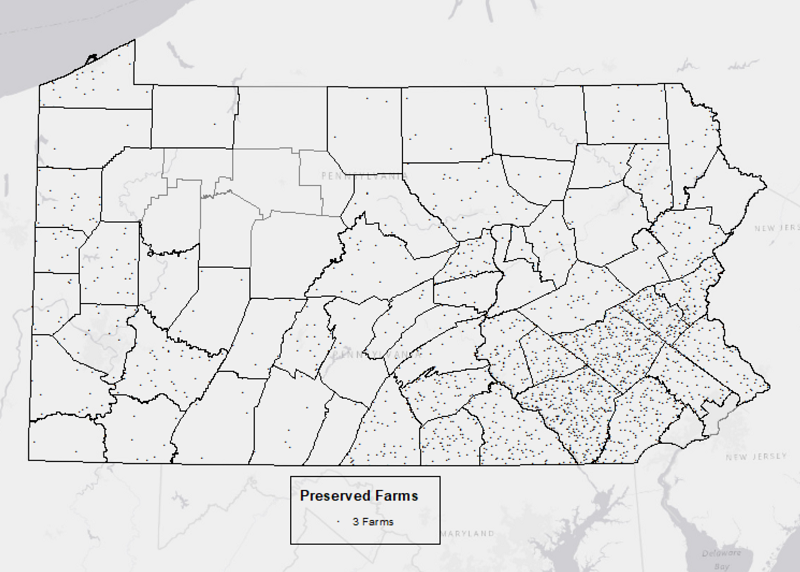
6. To prepare the map for final display, I added a basemap for improved context. I also added a second copy of the Counties layer in order to fill in the borders of the counties that were not drawn because they have no preserved farms. Notice the legend represented in the map above; it is not the ideal representation for a simple dot map like this; it is way too complicated and would be awkward to use for someone trying to read this map. A few adjustments were necessary to make it look like it does in the final version below.

Isoline Maps

Isoline Maps Represent Quantities

Understanding isolines was a very important part of learning about contour lines on topographic maps earlier in the course. If you recall, contour maps are constructed by a cartographer who starts with a set of point locations with an elevation at each point. The cartographer then decides on a set of contour values based on a contour interval, and interpolates the paths of the lines among those data points. Isolines can also be constructed for maps of air temperature, barometric pressure or some other (frequently environmental) data that represents a naturally continuous, ubiquitous phenomenon. In some cases the areas between the isolines are colored like a choropleth map to emphasize the increasing data values. A great example of this representation is the daily high temperature map in most newspapers.

The purpose of the isoline map is to divide the map area into zones of more similar values of the data variable, in this case precipitation. These zones do not follow boundary lines, like they do with the choropleth map, but follow lines determined by the data itself. When the data represent land elevations, you see an approximation of the hilliness of the landscape. The isolines that circle back on themselves, and that are nested inside other circling isolines represent the hill tops and mountain tops. You can apply that same metaphor to the other types of data; in the sample map for this page it becomes easy to find the small areas of highest precipitation.

Another scenario for the use of isoline maps is to depict non-environmental data variables representing a ratio or density (never a count) for a set of area features. Given our procedure for creating contour lines, this may sound counter-intuitive, because we would not be starting from point locations. However, there is a procedure for turning a set of area features into point locations by determining the point location at the center of each area. These points are known as "centroids" and ArcGIS does include a procedure for generating them automatically. In this case, we will just assume that we have been given such a layer, which includes the appropriate data variable in the attribute table for the layer. This image shows such a set of county centroids for the northeastern United States.

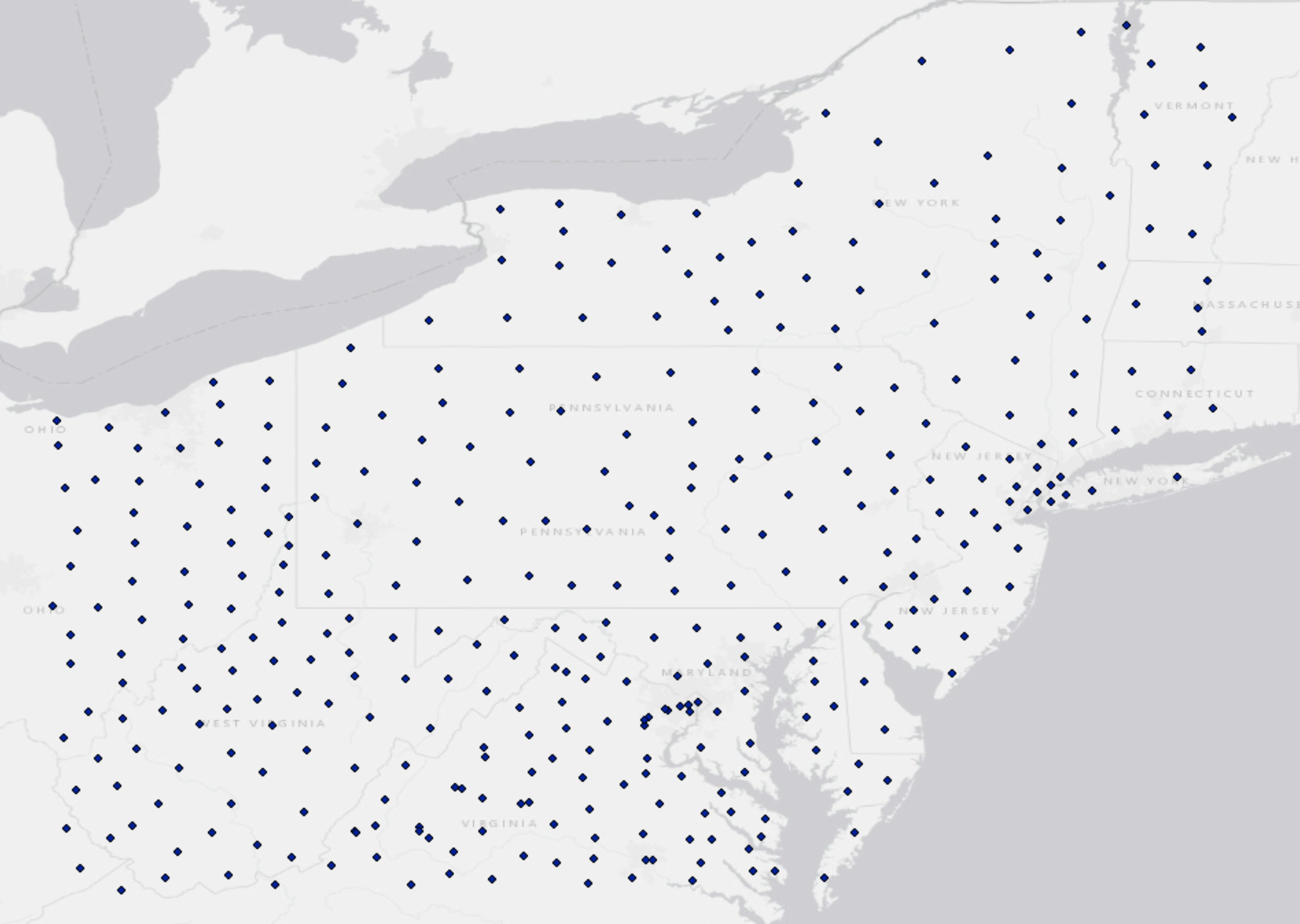
Creating Isoline Maps

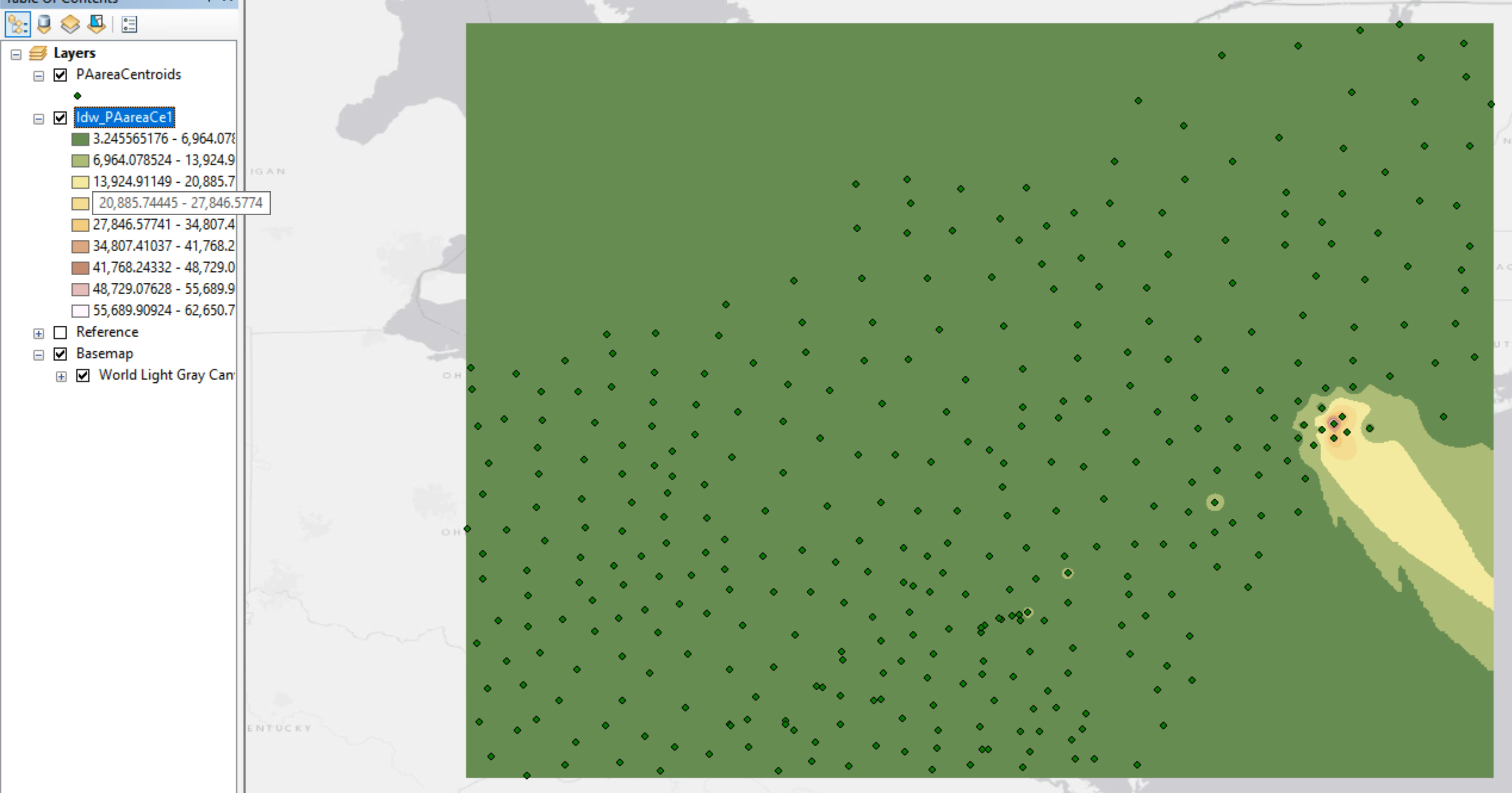
The Centroids layer can be used to create an isoline map of population density across the northeastern US, which can also illustrate some of the pitfalls of isoline mapping in ArcGIS (and in general). The next image below shows the output of the easiest procedure built into ArcMap to generate an isoline map; there are more options than this for different purposes, but the steps get much more complex. The map produced following this procedure is a raster layer, not a line layer of the isolines. ArcMap automatically adds the choropleth coloring between the isolines, and by default it chooses a color scheme that would be better suited to showing elevation contours; you can change that color scheme, though it can be hard to get an ideal mix of colors. It becomes another balancing act between competing considerations: the contour interval determines the number of different contour lines, which determines the number of different colors. Fewer colors are easier to distinguish but will show less detail, as on the map below. Another difficulty illustrated in the image below is that ArcMap creates the isolines based on the points layer, but does not "know" that areas with no points are oceans. It has to assume that whatever pattern it has created within the area covered by points extends outward. Again, in a higher level GIS course you will learn techniques for "clipping" the map to the edge of the continent.

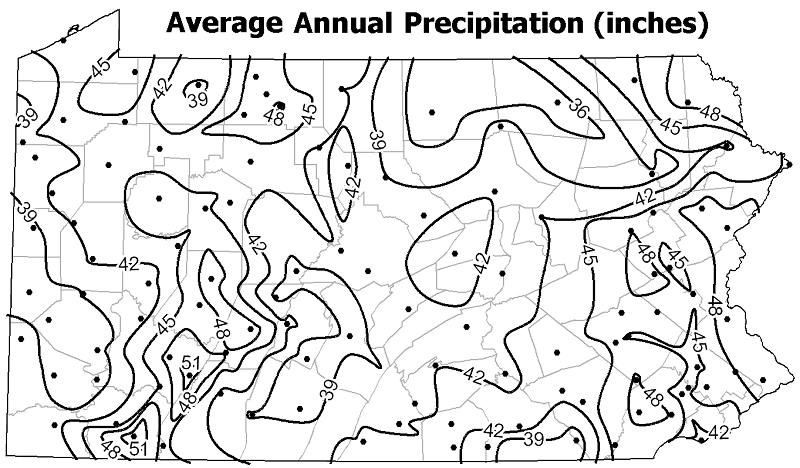
The isoline map below shows the average precipitation across Pennsylvania. I left the locations at which the precipitation was measured, which represent weather stations, on the map; usually the point features used to generate the isolines are not visible on the final map. The map is titled "Average Annual Precipitation," so at each of those locations the weather station had been recording precipitation totals for each year over several decades. Those were the starting data values. The decision about the isoline interval was to create a new isoline for every three inches of rainfall. I could have set the interval at every two inches, but that would have resulted in a very busy map; I could have set it at every five inches, but there would have been significantly fewer lines and it would have been harder to see the trends. The range of precipitation totals across Pennsylvania is between just below 36 inches (in north-central PA) and just above 51 inches (near southwestern PA).

The interpolation process mentioned above is essentially what you learned to execute on paper in the course. ArcGIS contains the ability to duplicate that procedure when given a layer of point locations that includes an appropriate data value. In fact, ArcGIS refers to the procedure as "contouring." As you did in your manual version of the process, the cartographer must tell ArcGIS the starting data value and the "contour interval." The software then positions each isoline relative to the given point locations and values.

There are just too many controls and considerations in the process to create an isoline map in ArcMap to be able to show that process easily here. One of those complications is that creating isolines in this manner requires a set of geoprocessing tools that must be added to "extend" the ArcGIS software The Spatial Analyst Extension includes a set of Interpolation tools; recall that interpolation was the term used to describe the process of estimating the positions of contours between control points in the process of constructing contour maps. Many things about the data processing and the output are awkward to try to make simple and clean. Save that process for your next GIS course.

Cartograms

Cartograms Show Quantities

Cartograms are the most elaborate of the thematic maps, approaching pure art. A cartogram represents count data only, again for area features such as the US states. A common data variable to use is the population of each area. Instead of varying the color of each state as is done for a choropleth map, the cartographer alters the size of each state according to its data value. Essentially, the cartographer is establishing a mathematical relationship between the data value and the state area. The artistic effect has to be added because, looking at any pair of neighboring states, state A might have a data value that is greater than state B, when in fact state A is actually smaller than its neighbor. The cartographer must introduce distortion of the shapes of each state in order to make the whole country fit together (sort of). See the example linked below. There are variations on this style of cartogram that rely less on keeping the states connected to each other, but the style depicted below tends to have maximum impact.

The website link below connects to a site that shows political election results using cartograms. What can be deceptive in this case is that the cartogram is based on states (or counties) distorted to the counts of Electoral College “electors” or election voters; the states (or counties) are then colored according to the party winning the vote count in that state (or county). The cartographer is thereby combining the cartogram with a choropleth map.

Cartograms from GIS Software

GIS software, at least as it comes "out of the box," is unable to create the cartogram. There are algorithms created to accomplish it, but they tend to take a long time to run. If you understand that asking a program that was designed to create mapped representations of real boundaries with very precisely located coordinates to now move those coordinates and create very unrealistic representations, you get a sense of why these are challenging for the software. Add to that the fact that many viewers of cartograms have trouble seeing the purpose of them or the data being represented, then that adds to the lack of appeal.

Heat Map

Context

Heat maps are a relatively new map design concept that has uses beyond the geographical map. Consider as a "default" a landscape in which any point location is equally likely, at least at some abstract or theoretical level, to have an occurrence of the data theme. The data are simple point locations with no attention paid to attribute data values. The theme could be earthquakes, tornado touchdowns, property sales, or crimes. The purpose of the heat map is to represent the relative density of the features, to identify "hot spots" or areas where that density is higher than those default conditions. Because of the calculations necessary to work that out, the heat map is categorized at the quantitative level of measurement.

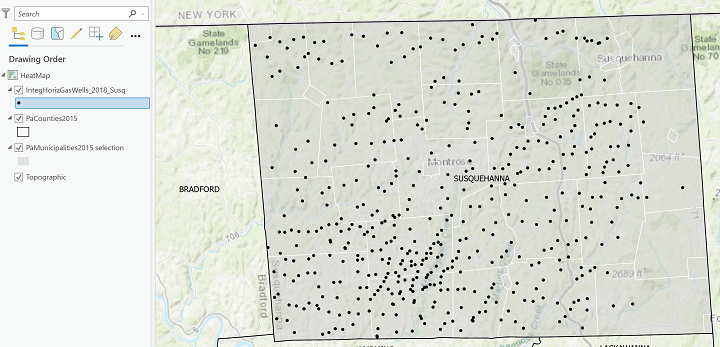
Here is an example of the starting data for such a map: this map shows oil and natural gas wells in one county Susquehanna County) in northern Pennsylvania for which the controversial procedure known as "fracking" (hydraulic fracturing) has been used. This map shows the well locations as simple black dots. It is a little deceptive because many of the apparent black dots are actually two or more separate dots spaced very closely together.

The Heat Map

Here is the Heat Map corresponding to the above map of fracked wells. Compare the well locations from the map above with the shades of color on this map.

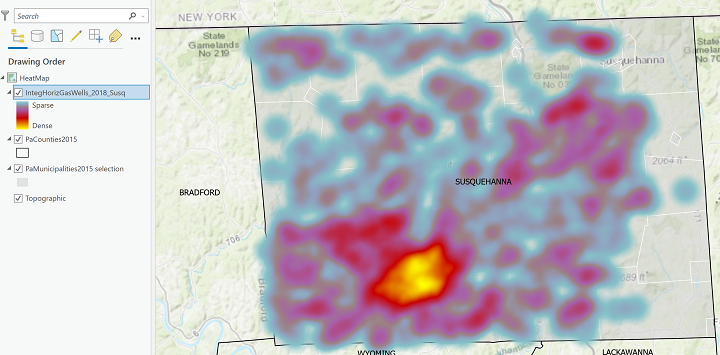
The heat map representation of those dots uses a color scheme that expresses a range of value from a minimum, say blue, to a maximum, like a bright red. For every location (including locations that have no dots), spaced a certain distance apart, the algorithm counts the number of data theme occurrences (or dots) within a fixed distance of that location. The occurrences (dots) are "counted" multiple times, but the shifting of the count locations means that some areas of the map will have much higher count values than others. Following the counting stage, the minimum and maximum numbers of occurrences are established as the lowest (coolest) and highest (hottest) values, respectively. That range of counts is made equivalent to the corresponding range of colors, which are then applied to the map at the count locations. Like the choropleth map, the heat map is using the "color ramp" idea to convey increasing density; unlike the choropleth map, there are no fixed boundaries for the colors, just the gradually shifting locations of the counts.

Unfortunately, this is another one of the types of thematic maps that you will not learn how to make with ArcMap. It is technically possible to create it using ArcMap but again requires advanced "extensions" to the program and an understanding of ArcGIS's "geoprocessing tools" system, which is beyond the scope of this course.