Divisibility

You probably know that division can be defined in terms of multiplication. If m and n are integers, m divides n if $n = mk$ for some integer k. In this section, I'll look at properties of the divisibility relation.

I'll begin by discussing the Division Algorithm, which tells you something you've known since grade school --- namely, that you can divide one integer by another. Note that this isn't the long-division algorithm, which tells you how to divide one integer by another. The Division Algorithm follows from the Well-Ordering Axiom for the nonnegative integers.

Well-Ordering Axiom. The positive integers $\integer^+$ are well-ordered --- that is, every nonempty subset of the positive integers has a smallest element.

Even though your experience with the integers may lead you to think this is obvious, it's actually an axiom of the positive integers $\integer^+$ . It has many important consequences; mathematical induction is one, and the Division Algorithm is another.

Note that Well-Ordering applies to nonempty subsets of the nonnegative integers as well. If such a subset contains 0, then 0 is the smallest element; if the subset doesn't contain 0, then it consists of only positive integers, and Well-Ordering for the positive integers implies that it has a smallest element.

Example. ( Applying the Well-Ordering Axiom) Show that there is no positive integer less than 1.

In this proof, I'm going to assume familiar facts about inequalities involving integers, since the point is to illustrate how you might use Well-Ordering.

Suppose that there is a positive integer less than 1. Let S be the set of positive integers less than 1. Then S is nonempty, so by Well-Ordering, S has a smallest element.

Suppose that x is the smallest element of S. Now $0 < x < 1$ , so multiplying by x, I get

$$0 < x^2 < x, \quad\hbox{and}\quad x < 1, \quad\hbox{so}\quad 0 < x^2 < x < 1.$$

Thus, $x^2$ is a positive integer less than 1 which is smaller than x. This is a contradiction. Therefore, there is no positive integer less than 1.

Theorem. ( The Division Algorithm) Let a and b be integers, with $b > 0$ . There are unique integers q and r such that

$$a = b \cdot q + r, \quad\hbox{and}\quad 0 \le r < b.$$

Of course, q is the quotient and r is the remainder.

Proof. What is division? Division is successive subtraction. Therefore, you ought to be able to find r by subtracting multiples of b from a until the result becomes negative. For example, if you're dividing 23 by 7, you'd do this:

$$23 - 7 = 16, \quad 23 - 2 \cdot 7 = 9, \quad 23 - 3 \cdot 7 = 2, \quad 23 - 4 \cdot 7 = -5. \quad\hbox{(Negative!)}$$

The quotient is 3 --- the last multiple of 7 which gave a nonnegative result. The last nonnegative result is the remainder, which is 2.

To do the proof, I have to take the idea exhibited in this example and write it out in general (with a, b, q, and r instead of specific numbers).

Look at the set of integers

$$S = \{a - bn \mid n \in \integer\}.$$

If I choose $n < \dfrac{a}{b}$ (as I can --- there's always an integer less than any number), then $b n < a$ , so $a - bn > 0$ . This choice of n produces a positive integer $a - b n$ in S. So the subset T consisting of nonnegative integers in S is nonempty.

Since T is a nonempty set of nonnegative integers, I can apply Well-Ordering. It tells me that there is a smallest element $r \in T$ . Thus, $r \ge 0$ , and $r = a - b q$ for some q (because $r \in T$ , $T \subset S$ , and everything in S has this form).

Moreover, if $r \ge b$ , then $r - b \ge 0$ , so

$$a - b q - b \ge 0, \quad\hbox{or}\quad a - b(q + 1) \ge 0.$$

So $a - b(q + 1) \in T$ , but $r = a - b q > a - b(q + 1)$ . This contradicts my assumption that r was the smallest element of T.

All together, I now have r and q such that

$$a = b \cdot q + r, \quad\hbox{and}\quad 0 \le r < b.$$

To show that r and q are unique, suppose $r'$ and $q'$ also satisfy these conditions:

$$a = b \cdot q' + r', \quad\hbox{and}\quad 0 \le r' < b.$$

Then

$$b \cdot q + r = b \cdot q' + r', \quad\hbox{so}\quad b(q - q') = r' - r.$$

But r and $r'$ are two nonnegative numbers less than b, so they are both in the range $0 \le x < b$ . Therefore, they have to be less than b units apart. But the last equation says they are $|b(q - q')|$ units apart --- a multiple of b).

The only way r and $r'$ can be less than b units apart and a multiple of b units apart is if the multiple in question is 0. That is, $|b(q - q')| = 0$ . Since $b > 0$ , this means that $q - q' = 0$ , or $q = q'$ . If I plug $q = q'$ back into $b(q - q') = r' - r$ , I find that $r' - r = 0$ , so $r = r'$ . This proves that r and q are unique.

Example. ( Applying the Division Algorithm) (a) Find the quotient and remainder when the Division Algorithm is applied to divide 99 by 13.

(b) Find the quotient and remainder when the Division Algorithm is applied to divide -99 by 13.

(a)

$$99 = 7 \cdot 13 + 8.$$

The quotient is 7 and the remainder is 8. According to the proof of the theorem, 8 should be the smallest positive number of the form $99 + k\cdot 13$ . In this case,

$$8 = 99 + (-7) \cdot 13.$$

Clearly, adding multiples of 13 to $99 + (-7)\cdot 13$ will give numbers larger than 8, whereas subtracting multiples of 13 from $99 + (-7)\cdot 13$ will give negative numbers.

(b)

$$-99 = (-8) \cdot 13 + 5.$$

Note that $0 \le 5 < 13$ . I don't write $-99 = (-7) \cdot 13 + -8$ (even though the equation is correct), because -8 is not between 0 and 13. The Division Algorithm always produces a nonnegative remainder.

Definition. If m and n are integers, then m divides n if $m k = n$ for some integer k.

The notation $m \mid n$ means that m divides n; $m \notdiv n$ means that m does not divide n.

Remarks. (a) Some people prefer to require that $m \ne 0$ when you write "$m \mid n$ ". Note that if $m = 0$ and $m \mid n$ , then $0 \mid n$ . This means $0 \cdot k = n$ for some k, so $n = 0$ . So the only divisibility statement you can make of the form "$0 \mid n$ " is "$0 \mid 0$ ", which isn't that interesting.

This issue is different from the idea that "you can't divide by 0", which means that 0 does not have a multiplicative inverse. We'll see later that in any commutative ring with identity, $0^{-1}$ can't be defined (unless the ring is the zero ring).

The definition of divisibility above makes no reference to multiplicative inverses or an operation of division: It's defined entirely in terms of multiplication.

(b) Be careful not to write "$\dfrac{n}{m}$ ", "$n/m$ ", or "$n \div m$ " when you mean "$m \mid n$ "!

"$\dfrac{n}{m}$ ", "$n/m$ ", and "$n \div m$ " all mean "n divided by m". Notice that this isn't a statement, since it's not a complete sentence that can be true or false --- it's an expression. On the other hand, "$m \mid n$ " means "m divides n", which is a statement.

Example. Apply the definition of divisibility to show that:

(a) $6 \mid 72$ .

(b) $-8 \mid 24$ .

(c) $1 \mid n$ for all $n \in \integer$ .

(d) $n \mid 0$ for all $n \in \integer$ .

(a) Since $6 \cdot 12 = 72$ , I have $6 \mid 72$ .

(b) Since $(-8) \cdot (-3) = 24$ , I have $-8 \mid 24$ .

(c) Since $1 \cdot n = n$ , I have $1 \mid n$ for all $n \in \integer$ .

(d) Since $n \cdot 0 = 0$ , I have $n \mid 0$ for all $n \in \integer$ .

Proposition.

(a) Let $m, n \in \integer$ . If $m \mid n$ and $n \mid p$ , then $m \mid p$ .

(b) Let $m, n, p \in \integer$ . If $m \mid n$ and $m \mid p$ , then $m \mid a n + b p$ for all $a, b \in \integer$ .

This is often expressed by saying that if m divides two numbers, it divides any integer linear combination of the two numbers.

(c) Let $m, n \in \integer$ . If $m \mid n$ , then $m \mid a n$ for all $a \in \integer$ .

(d) Let $m, n, p \in \integer$ . If $m \mid n$ and $m \mid p$ , then $m \mid n + p$ .

This is often expressed by saying that if m divides two numbers, it divides their sum. It's also true that if m divides two numbers, it divides their difference.

(e) If $m \mid n$ and $m, n \in \integer^+$ , then $m \le n$ .

Proof. The idea in divisibility proofs is often to translate statements like "$m \mid n$ " into equations like "$m k = n$ ", then work with the equations.

(a) $m \mid n$ implies $mk = n$ for some k. $n \mid p$ implies $nj = p$ for some j. Substituting the first equation into the second gives

$$(m k) j = p, \quad\hbox{i.e.}\quad m (k j) = p.$$

Therefore, $m \mid p$ .

(b) $m \mid n$ implies $m j = n$ for some j. And $m \mid p$ implies $m k = p$ for some k. Then

$$a n + b p = a (m j) + b (m k) = n (a j + b k).$$

Hence, $m \mid a n + b p$ .

(c) Taking $b = 0$ and $p = 0$ in (b), I find that $m \mid n$ and $m \mid 0$ implies

$$m \mid a n + 0 \cdot 0 = a n.$$

(d) Taking $a = b = 1$ in (b), I find that $m \mid n$ and $m \mid p$ implies

$$m \mid 1 \cdot n + 1 \cdot p = n + p.$$

(e) Suppose $m \mid n$ and $m, n \in \integer^+$ . $m \mid n$ implies $m k = n$ for some $k \in \integer$ ; k must be a positive integer, since m and n are positive integers. Thus, $k \ge 1$ , and multiplying both sides of this inequality by m gives

$$n = m k \ge m.\quad\halmos$$

Example. ( Proving a divisibility property) (a) Give an example of integers m and n such that $\mid n$ and $n \mid n$ but $m \ne n$ .

(b) Prove that if m and n are positive integers, $m \mid n$ , and $n \mid m$ , then $m = n$ .

(a) $7 \mid -7$ and $-7 \mid 7$ , but $7 \ne -7$ .

(b) One approach is to use property (e) of the preceding lemma. Since m and n are positive integers, $m \mid n$ implies $m \le n$ , and $n \mid m$ implies $n \le m$ . The two inequalities imply that $m = n$ .

Here's another proof which uses the definition of divisibility.

Since $m \mid n$ , $m a = n$ for some $a \in \integer$ . Since $n \mid m$ , $n b = m$ for some $b \in \integer$ . Hence, $m (a b) = m$ . Since $m > 0$ , I may cancel it from both sides to obtain $a b = 1$ .

a and b are integers, so either $a = b = 1$ or $a = b = -1$ . But if $a = -1$ , then $m\cdot (-1) = n$ , which is impossible since m and n are positive. Therefore, $a = 1$ , so $m = n$ .

Example. ( Even and odd integers) An integer $n \in \integer$ is even if $2 \mid n$ . An integer is odd if it is not even.

(a) Prove that even integers can be written in the form $2 m$ for some $m \in \integer$ , and odd integers can be written in the form $2 m + 1$ for some $m \in \integer$ .

(b) Prove that if $n \in \integer$ is even, so is $n^2 + 5 n + 6$ .

If n is even, then $2 \mid n$ , so $2 m = n$ for some $m \in \integer$ .

Suppose n is odd. Use the Division Algorithm to divide n by 2, obtaining a quotient of m and a remainder of r:

$$n = 2 m + r, \quad\hbox{where}\quad 0 \le r < 2.$$

Now $0 \le r < 2$ implies that $r = 0$ or $r = 1$ . If $r = 0$ , the equation says $n = 2 m$ , which means that n is even. But n was odd, so this is a contradiction. Therefore, $r = 1$ , and $n = 2 m + 1$ .

(b) Suppose $n \in \integer$ is even. By (a), $n = 2 m$ for some $m \in \integer$ . Then

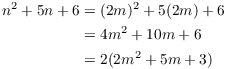
$$\eqalign{ n^2 + 5 n + 6 & = (2 m)^2 + 5 (2 m) + 6 \cr & = 4 m^2 + 10 m + 6 \cr & = 2 (2 m^2 + 5 m + 3) \cr}$$

I've expressed $n^2 + 5 n + 6$ as 2 times an integer, so $n^2 + 5 n + 6$ is even.

Note: In this proof, I'm only using properties of divisibility and the definition of "even". So (for instance) I can't stop with "$4 m^2 + 10 m + 6$ " and say that "the sum of even numbers is even", because I haven't proven yet that the sum of even numbers is even.

Example. Is there an integer n such that $7 \mid n^2 + n + 1$ and $7 \mid n + 1$ ?

No. Assume that $7 \mid n^2 + n + 1$ and $7 \mid n + 1$ for some n. Then 7 must divide any integer linear combination of $n^2 + n + 1$ and $n + 1$ , so

$$7 \mid (n^2 + n + 1) - n (n + 1) = n^2 + n + 1 - n^2 - n = 1.$$

This contradiction shows that there is no such n.

Example. Prove that if m is a positive integer and n is an integers such that $m \mid 4 n + 7$ and $m \mid 3 n + 5$ , then $m = 1$ .

One of the divisibility properties implies that m must divide any integer linear combination of $4 n + 7$ and $3 n + 5$ . So the idea is to construct a linear combination of $4 n + 7$ and $3 n + 5$ which adds up to 1. If this is to happen, the n's have to cancel; one way to get this to happen is to switch the "4" and the "3" and negate one of them:

$$m \mid 3 (4 n + 7) - 4 (3 n + 5) = 1.$$

Since m is a positive integer which divides 1, I must have $m = 1$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga