Finitely Generated Abelian Groups

There is no (known) formula which gives the number of groups of order n for any . However, it's possible to classify the finite abelian groups of order n. This classification follows from the structure theorem for finitely generated abelian groups.

Definition. Let G be an abelian group. The torsion subgroup of G is

$T = \{g \in G \mid n g = 0 \hbox{ for some } n \in \integer^+\}.$

I'd better check that the definition makes sense!

Proposition. Let G be an abelian group. The torsion subgroup of G is a subgroup of G.

Proof. Let T be the torsion subgroup of G. $0 \in T$ , so T is nonempty. Let $a, b \in T$ . I must show $a - b \in T$ . Find positive integers m, n, such that and . Then

Therefore, $a - b \in T$ , and .

Definition. A group G is torsion free if the only element of finite order is the identity.

Definition. An abelian group G is finitely generated if there are elements $x_1, \ldots, x_n \in G$ such that every element $x \in G$ can be written as

$x = a_1 x_1 + \cdots + a_n x_n, \qquad a_i \in \integer.$

Note that this expression need not be unique.

Definition. A free abelian group is a direct sum of copies of $\integer$ (possibly infinitely many copies).

The number of copies (in the sense of cardinality) is the rank of the free abelian group. It's possible to prove that the rank of a free abelian group is well-defined.

Theorem. Let G be a finitely generated abelian group.

(a) $G = T \times F$ , where T is the torsion subgroup and F is a free abelian group.

(b) The rank of F is uniquely determined by G.

(c) The torsion part T can be written as a direct sum of cyclic groups in the following ways. Each decomposition is unique (in the first case, up to the order of the factors):

$T \approx \integer_{{p_1}^{r_1}} \times \integer_{{p_2}^{r_2}} \times \cdots \times \integer_{{p_n}^{r_n}}.$

$T \approx \integer_{d_1} \times \integer_{d_2} \times \cdots \times \integer_{d_m}, \qquad 1 \le d_1 \mid d_2 \mid \cdots \mid d_m.$

In the first case, the p's are primes (not necessarily distinct), and for all i. The first case is called a primary decomposition while the second case is called an invariant factor decomposition.

The proof of this result is outside the scope of this course. But I should mention that it is related to the Jordan canonical form and rational canonical form that you may have seen in linear algebra. The structure theorem for finitely generated abelian groups and the results on canonical forms are special cases of a more general structure theorem: The structure theorem for finitely generated modules over a principal ideal domain.

$\matrix{& & \matrix{\hbox{structure theorem} \cr \hbox{for} \cr \hbox{finitely generated modules} \cr \hbox{over a PID} \cr} & & \cr & \swarrow & & \searrow & \cr \matrix{\hbox{structure theorem} \cr \hbox{for} \cr \hbox{finitely generated} \cr \hbox{abelian groups} \cr} & & & & \matrix{\hbox{rational and Jordan} \cr \hbox{canonical forms} \cr} \cr}$

Let's concentrate for now on the case of a finite abelian group. Since any factor of $\integer$ would make the group infinite, there can't be any $\integer$ 's in the decomposition. The result then says that every finite abelian can be written as

$\integer_{{p_1}^{r_1}} \times \integer_{{p_2}^{r_2}} \times \cdots \times \integer_{{p_n}^{r_n}}.$

Here the p's are primes and the r's are positive integers ( primary decomposition).

Alternatively, you can write the same group as

$\integer_{d_1} \times \integer_{d_2} \times \cdots \times \integer_{d_m}.$

In this case, the d's are positive integers and $d_1 \mid \cdots \mid d_m$ ( invariant factor decomposition).

Example. ( Listing all the primary and invariant factor decompositions) Find the primary decompositions and corresponding invariant factor decompositions for all abelian groups of order 360.

First, factor 360 into a product of primes: $360 = 2^3\cdot 3^2\cdot 5$ .

Next, write each prime power in all possible ways:

$2^3: \quad 2^3, 2\cdot 2^2, 2\cdot 2\cdot 2$

$3^2: \quad 3^2, 3\cdot 3$

$5: \quad 5$

You get the primary decompositions by using one of the factorizations, one of the factorizations, and the lone 5. I'll list the possibilities below, together with the corresponding invariant factor decompositions.

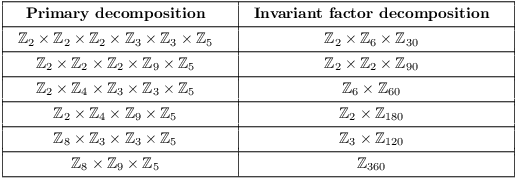
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & {\bf Primary decomposition} & & {\bf Invariant factor decomposition} & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_2\times \integer_2\times \integer_2\times \integer_3\times \integer_3\times \integer_5$ & & $\integer_2\times \integer_6\times \integer_{30}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_2\times \integer_2\times \integer_2\times \integer_9\times \integer_5$ & & $\integer_2\times \integer_2\times \integer_{90}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_2\times \integer_4\times \integer_3\times \integer_3\times \integer_5$ & & $\integer_6\times \integer_{60}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_2\times \integer_4\times \integer_9\times \integer_5$ & & $\integer_2\times \integer_{180}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_8\times \integer_3\times \integer_3\times \integer_5$ & & $\integer_3\times \integer_{120}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & $\integer_8\times \integer_9\times \integer_5$ & & $\integer_{360}$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }}$

The two groups in each row are isomorphic --- they're "the same" as groups.

Here's an example which shows how I got the invariant factor decompositions. Consider $\integer_2\times \integer_2\times \integer_2\times \integer_3\times \integer_3\times \integer_5$ . Write the numbers for each prime in a row, right-justified:

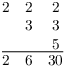
$\matrix{2 & 2 & 2 \cr & 3 & 3 \cr & & 5 \cr \noalign{\vskip2 pt\hrule\vskip2 pt} 2 & 6 & 30 \cr}$

Multiply the numbers in each column. These give the numbers for the invariant factor decomposition. Note that 2 divides 6 and 6 divides 30.

Example. ( Finding the primary and invariant factor decompositions for a specific group) Find the primary decomposition and invariant factor decomposition for $\integer_4\times \integer_{12}\times \integer_{18}$ .

First, I take each of the factors apart into direct products of groups of prime power order.

$\integer_4\times \integer_{12}\times \integer_{18} \approx \integer_4\times (\integer_4\times \integer_3)\times (\integer_2\times \integer_9).$

I'm using the fact that $\integer_m\times \integer_n \approx\integer_{mn}$ if and only if m and n are relatively prime. Thus, $\integer_{12} \approx \integer_4\times \integer_3$ because 3 and 4 are relatively prime.

I can't replace $\integer_4$ with $\integer_2\times \integer_2$ because 2 is not relatively prime to 2 (2 and 2 have the common factor 2!).

Thus, the primary decomposition is

$\integer_2\times \integer_4\times \integer_4\times \integer_3\times \integer_9.$

Next, I find the invariant factor decomposition:

$\matrix{ 2 & 4 & 4 \cr & 3 & 9 \cr \noalign{\vskip2 pt\hrule\vskip2 pt} 2 & 12 & 36 \cr}$

So the invariant factor decomposition is

$\integer_2\times \integer_{12}\times \integer_{36}.$

Note that 2 divides 12 and 12 divides 36.

Example. ( Finding primary decompositions satisfying a condition on orders of elements) Suppose G is an abelian group of order 24, and no element has order greater than 12. What are the possible primary decompositions for G?

Since $24 = 2^3\cdot 3$ , the primary decompositions for abelian groups of order 24 are

$\integer_8 \times \integer_3, \quad \integer_2 \times \integer_4 \times \integer_3, \quad \integer_2 \times \integer_2 \times \integer_2 \times \integer_3.$

Let $(a, b, c) \in \integer_2 \times \integer_4 \times \integer_3$ . Then

Therefore, no element of $\integer_2 \times \integer_4 \times \integer_3$ has order greater than 12.

Let $(a, b, c, d) \in \integer_2 \times \integer_2 \times \integer_2 \times \integer_3$ . Then

Therefore, no element of $\integer_2 \times \integer_2 \times \integer_2 \times \integer_3$ has order greater than 12.

However, for $(1, 1) \in \integer_8 \times \integer_3$ , I have

$12(1, 1) = (4, 0) \ne (0, 0).$

So does not have order less than 12 --- in fact, it has order 24.

Therefore, the possible primary decompositions for G are $\integer_2 \times \integer_4 \times \integer_3$ and $\integer_2 \times \integer_2 \times \integer_2 \times \integer_3$ .

Contact information

Bruce Ikenaga's Home Page