Group Homomorphisms

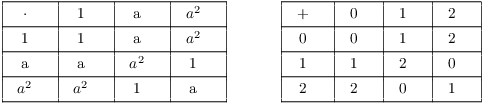
Here are the operation tables for two groups of order 4:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 1 & & a & & $a^2$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & a & & $a^2$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & a & & a & & $a^2$ & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $a^2$ & & $a^2$ & & 1 & & a & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.5in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 0 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

There is an obvious sense in which these two groups are "the same": You can get the second table from the first by replacing 0 with 1, 1 with a, and 2 with .

When are two groups the same?

You might think of saying that two groups are the same if you can get one group's table from the other by substitution, as above. However, there are problems with this. In the first place, it might be very difficult to check --- imagine having to write down a multiplication table for a group of order 256! In the second place, it's not clear what a "multiplication table" is if a group is infinite.

One way to implement a substitution is to use a function. In a sense, a function is a thing which "substitutes" its output for its input. I'll define what it means for two groups to be "the same" by using certain kinds of functions between groups. These functions are called group homomorphisms; a special kind of homomorphism, called an isomorphism, will be used to define "sameness" for groups.

Definition. Let G and H be groups. A homomorphism from G to H is a function $f: G \rightarrow H$ such that

$f(x \cdot y) = f(x) \cdot f(y) \quad\hbox{for all}\quad x, y \in G.$

Group homomorphisms are often referred to as group maps for short.

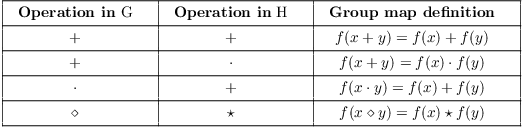
Remarks. 1. In the definition above, I've assumed multiplicative notation for the operations in both G and H. If the operation in one or both is something else, you must adjust the definition accordingly. For instance:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & {\bf Operation in} G & & {\bf Operation in} H & & {\bf Group map definition} & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & + & & + & & $f(x + y) = f(x) + f(y)$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & + & & $\cdot$ & & $f(x + y) = f(x) \cdot f(y)$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\cdot$ & & + & & $f(x \cdot y) = f(x) + f(y)$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $\diamond$ & & $\star$ & & $f(x \diamond y) = f(x) \star f(y)$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

2. You have seen patterns like this before; for example, "The derivative of a sum is the sum of the derivatives".

Lemma. Let G be a group and let H be a subgroup.

(a) The identity map $\id: G \to G$ defined by $\id(x) = x$ is a group map.

(b) The inclusion map $i: H \to G$ defined by $\i(x) = x$ is a group map.

Proof. I'll prove (a); the proof of (b) is the same. Let $x, y \in G$ . Then

$\id(x \cdot y) = x \cdot y = \id(x) \cdot \id(y).$

Hence, $\id$ is a group map.

Example. ( Constant maps are usually not group maps) For the group $\integer$ under addition, define $f: \integer \rightarrow \integer$ by

$f(n) = 3 \quad\hbox{for all}\quad n \in \integer.$

Show that f is not a group map.

$f(1 + 1) = f(2) = 3, \quad\hbox{but}\quad f(1) + f(1) = 3 + 3 = 6.\quad\halmos$

Example. ( Logs and exponentials) (a) Prove that the exponential function $\exp: (\real,+) \to (\real^+,\cdot)$ given by $\exp(x) = e^x$ is a group map.

(b) Prove that the natural log function $\ln: (\real^+, \cdot) \to (\real, +)$ is a group map.

(a) Let $x, y \in \real$ . Then by properties of exponentials,

$\exp(x + y) = e^{x + y} = e^x \cdot e^y = \exp(y) \cdot \exp(y).\quad\halmos$

(b) Let $x, y \in \real^+$ . Then by properties of logarithms,

$\ln (x \cdot y) = \ln x + \ln y.\quad\halmos$

Example. ( Checking whether a function is a group map)

(a) Define $f: \integer \to \integer$ by

Prove or disprove: f is a group map.

(b) Define $g: \integer \to \integer$ by

Prove or disprove: f is a group map.

(a) f is a group map: If $x, y \in \integer$ , then

$f(x + y) = 5(x + y) = 5 x + 5 y = f(x) + f(y).\quad\halmos$

(b)

$g(2 + 3) = g(5) = 5^2 = 25, \quad\hbox{but}\quad g(2) + g(3) = 2^2 + 3^2 = 4 + 9 = 13.$

Since $g(2 + 3) \ne g(2) + g(3)$ , g is not a homomorphism.

Lemma. Let V and W be vector spaces over a field F, considered as groups under vector addition. Let $T: V \to W$ be a linear transformation. Then T is a group map.

Proof. This follows immediately from one of the axioms for a linear transformation: If $x, y \in V$ , then

$T(x + y) = T(x) + T(y).\quad\halmos$

Example. $\real^3$ and $\real^2$ are groups under vector addition. Define $T: \real^3 \to \real^2$ by

Prove that T is a group map.

Write T as a matrix multiplication:

$T\left(\left[\matrix{x \cr y \cr}\right]\right) = \left[\matrix{ 2 & 8 & -1 \cr 1 & 5 & -3 \cr}\right] \left[\matrix{x \cr y \cr}\right].$

From linear algebra, this defines a linear transformation. Hence, T is a group map by the previous lemma.

Example. ( A group map on a matrix group) Let $M(2, \real)$ be the group of $2 \times 2$ reals matrices under matrix addition. Let $\tr: M(2, \real) \to \real$ denote the trace map:

$\tr \left(\left[\matrix{a & b \cr c & d \cr}\right]\right) = a + d.$

Show that $\tr$ is a group homomorphism.

Now

$\tr \left(\left[\matrix{a & b \cr c & d \cr}\right] + \left[\matrix{a' & b' \cr c' & d' \cr}\right]\right) = \tr \left(\left[\matrix{a + a' & b + b' \cr c + c' & d + d' \cr}\right]\right) = (a + a') + (d + d'),$

$\tr \left(\left[\matrix{a & b \cr c & d \cr}\right]\right) + \tr \left(\left[\matrix{a' & b' \cr c' & d' \cr}\right]\right) = (a + d) + (a' + d').$

Thus,

$\tr\left(\left[\matrix{a & b \cr c & d \cr}\right] + \left[\matrix{a' & b' \cr c' & d' \cr}\right]\right) = \tr\left(\left[\matrix{a & b \cr c & d \cr}\right]\right) + \tr\left(\left[\matrix{a' & b' \cr c' & d' \cr}\right]\right).$

Therefore, $\tr$ is a homomorphism.

Lemma. Let $f: G \rightarrow H$ be a group homomorphism. Then:

(a) , where is the identity in G and is the identity in H.

(b) $f(x^{-1}) = f(x)^{-1}$ for all $x \in G$ .

Proof. (a)

$f(1_G) = f(1_G \cdot 1_G) = f(1_G)\cdot f(1_G).$

If I cancel off both sides, I obtain .

(b) Let $x \in G$ .

$f(x) \cdot f(x^{-1}) = f(x \cdot x^{-1}) = f(1_G) = 1_H$

$f(x^{-1}) \cdot f(x) = f(x^{-1} \cdot x) = f(1_G) = 1_H$

This shows that $f(x^{-1})$ is the inverse of , i.e. $f(x)^{-1} = f(x^{-1})$ .

Warning. The properties in the last lemma are not part of the definition of a homomorphism. To show that f is a homomorphism, all you need to show is that $f(a\cdot b) = f(a)\cdot f(b)$ for all a and b. The properties in the lemma are automatically true of any homomorphism.

On the other hand, if you want to show a function is not a homomorphism, do a quick check: Does it send the identity to the identity? If not, then the lemma shows it's not a homomorphism.

Example. ( Group maps must take the identity to the identity) Let $\integer$ denote the group of integers with addition. Define $f: \integer \to \integer$ by

Prove that f is not a group map.

Note that . Since the identity $0 \in \integer$ is not mapped to the identity $0 \in \integer$ , f cannot be a group homomorphism.

Warning: If a function takes the identity to the identity, it may or may not be a group map. Consider $g: \integer \to \integer$ given by

$g(x) = \sin x.$

$g(0) = \sin 0 = 0$ , but this doesn't mean that g is a homomorphism. In fact,

$g\left(\dfrac{\pi}{2} + \dfrac{\pi}{2}\right) = g(\pi) = \sin \pi = 0, \quad\hbox{but}\quad g\left(\dfrac{\pi}{2}\right) + g\left(\dfrac{\pi}{2}\right) = \sin \dfrac{\pi}{2} + \sin \dfrac{\pi}{2} = 1 + 1 = 2.$

The point is that simple-looking functions you may have seen in other math classes need not be homomorphisms. When in doubt, check the definition.

There are several important subsets associated to a group homomorphism $f: G \rightarrow H$ .

Definition. Let $f: G \rightarrow H$ be a group homomorphism.

(a) The kernel of f is

$\ker f = \{g \in G \mid f(g) = 1\}.$

(b) The image of f is (as usual)

$\im f = \{ f(g) \mid g \in G\}.$

$f^{-1}(H') = \{g \in G \mid f(g) \in H'\}.$

Warning. The notation $f^{-1}(H')$ does not imply that the inverse of f exists. $f^{-1}(H')$ is simply the set of inputs which f maps into ; this is $f^{-1}$ applied to the set if there is a $f^{-1}$ (but there need not be).

Lemma. Let $f: G \to H$ be a group map.

(a) $\ker f$ is a subgroup of G.

(b) $\im f$ is a subgroup of H.

Proof. (a) First,

$f(1) = 1, \quad\hbox{so}\quad 1 \in \ker f.$

Suppose $x, y \in \ker f$ . Then

$f(x y) = f(x)f(y) = 1 \cdot 1 = 1.$

Hence, $x y \in \ker f$ .

Finally, suppose $x \in \ker f$ . Then

$f(x^{-1}) = f(x)^{-1} = 1^{-1} = 1.$

Hence, $x^{-1} \in \ker f$ . Therefore, $\ker f$ is a subgroup of G.

(b) $1 \in \im f$ since .

Suppose $f(x), f(y) \in \im f$ . Then

$f(x) f(y) = f(x y) \in \im f.$

Finally, suppose $f(x) \in \im f$ . Then

$f(x)^{-1} = f(x^{-1}) \in \im f.$

Therefore, $\im f$ is a subgroup of H.

(c) Let be a subgroup of H. I want to show that $f^{-1}$ is a subgroup of G. Reminder: The criterion for membership in $f^{-1}(H')$ is that f takes the element into .

Since $1 \in H'$ and , it follows that $1 \in f^{-1}(H')$ .

Suppose $x, y \in f^{-1}(H')$ . This means that and are in . Since is a subgroup, is in as well. But

Therefore, is in , which means that $x y \in f^{-1}(H')$ .

Finally, suppose $x \in f^{-1}(H')$ , so $f(x) \in H'$ . Since is a subgroup, $f(x)^{-1} \in H'$ . But $f(x)^{-1} = f(x^{-1})$ , so $f(x^{-1}) \in H'$ . This means that $x^{-1} \in H'$ .

Hence, $f^{-1}(H')$ is a subgroup of G.

Example. ( Finding the kernel and image) (a) Let

$S^1 = \{z \in \complex \mid |z| = 1\}.$

Show that is a group under multiplication of complex numbers.

(b) Define $f: \real \rightarrow S^1$ by

$f(t) = e^{2 \pi i t}.$

Show that f is a group map, and find its kernel and image.

(a) Each element $z \in S^1$ can be uniquely written in the form

$z = e^{2 \pi i t} = \cos (2 \pi t) + i \sin (2 \pi t) \quad\hbox{for}\quad 0 \le t < 1.$

Note that

$e^{2 \pi i s} e^{2 \pi i t} = e^{2 \pi i (s + t)}.$

This shows that multiplication is closed (hence a binary operation) on S.

Complex number multiplication is associative. The identity element is 1; the inverse of $e^{2\pi it}$ is $e^{-2\pi it}$ .

(b) To see that f is a homomorphism, note that

$f(s + t) = e^{2 \pi i (s + t)} = e^{2 \pi i s} e^{2 \pi i t} = f(s) f(t).$

From the representation of elements of S as $e^{2 \pi i t}$ , I have $\im f = S^1$ .

The kernel of f is

$\ker f = \{ t \in \real \mid e^{2 \pi i t} = 1\}.$

Using $e^{2 \pi i t} = \cos (2 \pi t) + i \sin (2 \pi t)$ , you can see that $\ker f = \integer$ .

Example. ( Kernel, image, and inverse image) $f: \integer_8 \to \integer_{12}$ is defined by

$f(x) = 3 x \mod{12}.$

Take for granted that f is a group map. Find $\ker f$ , $\im f$ , and $f^{-1}(H)$ , where H is the subgroup $\{0, 6\}$ of $\integer_{12}$ .

The kernel consists of elements of $\integer_8$ which f takes to 0. Since 0 "is" 12 in $\integer_{12}$ , and since f multiplies inputs by 3, I'll get multiples of 12 out if I feed multiples of 4 in:

$f(0) = 0, \quad f(4) = 0.$

Hence, $\ker f = \{0, 4\}$ .

$\im f$ consists of the set of outputs of f. Since f multiplies its inputs by 3, the outputs are the multiples of 3:

$\im f = \{0, 3, 6, 9\}.$

Finally, $f^{-1}(\{0, 6\})$ consists of elements of $\integer_8$ which are mapped by f to either 0 or 6. So you need to find the elements in $\{0, 1, 2, 3, 4, 5, 6, 7\}$ which give 0 or 6 when multiplied by 3. Obviously, an "odd" input will give an "odd" output, and I already know 0 and 4 are mapped by f to 0, so I just try 2 and 6:

$f(2) = 6, \quad f(6) = 6.$

Hence, $f^{-1}(\{0, 6\}) = \{0, 2, 4, 6\}$ .

Definition. Let G and H be groups. An isomorphism from G to H is a bijective homomorphism $f: G \rightarrow H$ . If there is an isomorphism $f: G \rightarrow H$ , G and H are isomorphic; notation: $G \approx H$ .

Remarks. 1. To say that two groups are isomorphic is to say that they are the same as groups. The elements of the two groups and the group operations may be different, but the two groups have the same structure. This means that if one has a certain group-theoretic property, the other will as well.

What is a group-theoretic property? Well, it's a bit circular: a group-theoretic property is a property preserved by isomorphism. For this to be a useful concept, I'll have to provide specific examples of properties that you can check.

2. Some older books define an isomorphism from G to H to be an injective homomorphism $f: G \rightarrow H$ . That is, f need not map G onto H. One then says G and H are isomorphic if there is an isomorphism from G onto H. Unfortunately, one then has the odd situation that there may be an isomorphism from G to H, yet G and H may not be isomorphic! I'll always use the word isomorphism to mean a bijective map.

Here is an easy way to tell that a group map is an isomorphism.

Lemma. A group map $f: G \rightarrow H$ is an isomorphism if and only if it is invertible. In this case, $f^{-1}$ is also a homomorphism, hence an isomorphism.

Proof. The first statement is trivial, since a map of sets is bijective if and only if it has an inverse.

Now suppose that $f: G \rightarrow H$ is an isomorphism. I must show the inverse $f^{-1}: H \rightarrow G$ is a homomorphism. Let $x, y \in H$ . I need to show that

$f^{-1}(x y) = f^{-1}(x) f^{-1}(y).$

Since $f: G \rightarrow H$ is onto, there exist $x, y \in G$ such that and . Then

$f^{-1}(x y) = f^{-1}\left(f(x) f(y)\right) = f^{-1}\left(f(x y)\right) = x y = f^{-1}(x) f^{-1}(y).$

Therefore, $f^{-1}$ is a homomorphism.

Since $f^{-1}$ is invertible --- its inverse is f --- it is an isomorphism by the first part of the lemma.

Example. ( A group isomorphism) Show that the exponential map $\exp: (\real, +) \rightarrow (\real^+, \cdot)$ given by $\exp(x) = e^x$ is a group isomorphism.

I showed earlier that $\exp$ and the natural log function $\ln: \real^+ \to \real$ are group maps. They're also inverses:

$\ln (\exp(x)) = \ln e^x = x \quad\hbox{for}\quad x \in \real.$

$\exp(\ln x) = e^{\ln x} = x \quad\hbox{for}\quad x \in \real^+.$

By the lemma, $\exp$ is an isomorphism (as is $\ln$ ). The groups $(\real, +)$ and $\real^{+}$ are isomorphic.

Example. ( A group isomorphism on the integers mod 2) Consider the set $G = \{-1, 1\}$ . Make G into a group using multiplication as the group operation. Show that G is isomorphic to $\integer_2$ .

Define a map $f: \integer_2 \rightarrow G$ by

$f(0) = 1, \quad f(1) = -1.$

Clearly, f is invertible: Its inverse is

$f^{-1}(1) = 0, \quad f^{-1}(-1) = 1.$

I'll show f is a homomorphism, hence an isomorphism, by simply checking cases:

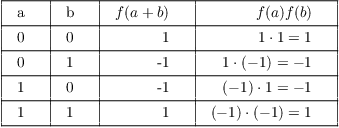
$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & a & & b & & $f(a + b)$ & & $f(a)f(b)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & $1\cdot1 = 1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 1 & & -1 & & $1\cdot(-1) = -1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & -1 & & $(-1)\cdot 1 = -1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & $(-1)\cdot(-1) = 1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

The brute force approach above can be used to construct an isomorphism from $\integer_2$ to any group of order 2. There is only one group of order 2, up to isomorphism.

Here are some examples of "group-theoretic properties". Thus, if two groups are isomorphic and one of the groups has such a property, the other must as well. On the other hand, if one of two groups has one of these properties but the other group does not, then the two groups cannot be isomorphic.

Proposition. Suppose G and H are isomorphic groups. If G is abelian, so is H.

Proof. Let $x, y \in H$ . I must show that . Since f is surjective, there exist $x', y' \in G$ such that and . Then

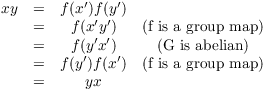
$\matrix{ x y & = & f(x') f(y') & \cr & = & f(x' y') & \hbox{(f is a group map)} \cr & = & f(y' x') & \hbox{(G is abelian)} \cr & = & f(y') f(x') & \hbox{(f is a group map)} \cr & = & y x & \cr}$

Therefore, H is abelian.

Example. ( Non-isomorphic groups) is the group of symmetries of an equilateral triangle. and $\integer_6$ are both groups of order 6. Why aren't they isomorphic?

$\integer_6$ is abelian, while is nonabelian. Therefore, and $\integer_6$ are not isomorphic.

Proposition. Suppose G and H are isomorphic groups. If G is finite, so is H. If G is infinite, so is H.

In other words, isomorphic groups have the same cardinality.

Proof. Since G and H are isomorphic, there is a bijective (group map) $f: G \to H$ . Since f is bijective, (since that's what it means for two sets to have the same cardinality).

Example. ( Groups of different cardinalities aren't isomorphic) Why can't $\integer$ and $\real$ be isomorphic?

Both groups are infinite, but the integers are countable, while the reals are uncountable. Since they don't have the same cardinality, they can't be isomorphic.

Proposition. Suppose G and H are isomorphic groups. If G has a subgroup K of order 42, so does H.

Proof. If and , then and (since f maps K bijectively onto ) .

Obviously, there's nothing special about "42". If G has a subgroup of order 117, so does H. If G has a subgroup of order 91, so does H. And so on. This proposition is not very useful as is, and is just here to show you a property shared by isomorphic groups.

There are clearly infinitely many properties that will be shared by isomorphic groups. However, the earlier examples show that some properties are not shared by isomorphic groups. For example, the elements of one group may be letters, while the elements of the other are numbers. "Having the same kind of elements" is not a group-theoretic property. Likewise, the operation in one group may be addition of numbers, while the operation in the other could be composition of functions. "Having the same kind of binary operation" is not a group-theoretic property.

Example. ( Showing groups aren't isomorphic by considering orders of elements)

(a) Show that $\integer_2 \times \integer_2$ and $\integer_4$ are not isomorphic.

(b) Show that $\integer_2 \times \integer_2 \times \integer_2$ , $\integer_2 \times \integer_4$ , and $\integer_8$ are not isomorphic.

(a) Both groups have 4 elements; however, every element of $\integer_2 \times \integer_2$ has order 1 or 2. If $(x, y) \in \integer_2 \times \integer_2$ , then

$2 \cdot (x, y) = (2 x, 2 y) = (0, 0).$

Therefore, the order of divides 2, and the only positive divisors of 2 are 1 and 2.

On the other hand, $\integer_4$ has two elements of order 4 (namely 1 and 3). Having different numbers of elements of a given order is a group property. Since these groups differ in this respect, they aren't isomorphic.

(b) $\integer_2 \times \integer_2 \times \integer_2$ , $\integer_2 \times \integer_4$ , and $\integer_8$ are all abelian groups of order 8. However, their elements have different orders.

Every element of $\integer_2 \times \integer_2 \times \integer_2$ has order 1 or 2. For if $(x, y, z) \in \integer_2 \times \integer_2 \times \integer_2$ , then

$2 \cdot (x, y, z) = (2 x, 2 y, 2 z) = (0, 0, 0).$

Therefore, the order of divides 2, and the only positive divisors of 2 are 1 and 2.

Every element of $\integer_2 \times \integer_4$ has order 1, 2, or 4. For if $(x, y) \in \integer_2 \times \integer_4$ , then

$4\cdot (x, y) = (4 x, 4 y) = (0, 0).$

Therefore, the order of divides 4, and the only positive divisors of 2 are 1, 2, and 4. Note that is an element of order 4. This means that $\integer_2 \times \integer_4$ can't be isomorphic to $\integer_2 \times \integer_2 \times \integer_2$ , since the latter has no elements of order 4.

$\integer_8$ has elements of order 8. (1 has order 8, for example.) Therefore, it can't be isomorphic to $\integer_2 \times \integer_2 \times \integer_2$ or to $\integer_2 \times \integer_4$ , since these two groups have no elements of order 8.

Therefore, the three groups aren't isomorphic.

Contact information

Bruce Ikenaga's Home Page