Polynomial Rings

If R is a ring, the ring of polynomials in x with coefficients in R is denoted $R[x]$ . It consists of all formal sums

$$\sum_{i=0}^\infty a_i x^i.$$

Here $a_i = 0$ for all but finitely many values of i.

If the idea of "formal sums" worries you, replace a formal sum with the infinite vector whose components are the coefficients of the sum:

$$\sum_{i=0}^\infty a_i x^i = (a_0, a_1, a_2, \ldots).$$

All of the operations which I'll define using formal sums can be defined using vectors. But it's traditional to represent polynomials as formal sums, so this is what I'll do.

A nonzero polynomial $\displaystyle \sum_{i=0}^\infty a_i x^i$ has degree n if $n \ge 0$ and $a_n \ne 0$ , and n is the largest integer with this property. The zero polynomial is defined by convention to have degree $-\infty$ . (This is necessary in order to make the degree formulas work out.) Alternatively, you can say that the degree of the zero polynomial is undefined; in that case, you will need to make minor changes to some of the results below.

Polynomials are added componentwise, and multiplied using the "convolution" formula:

$$\sum_{i=0}^\infty a_i x^i + \sum_{i=0}^\infty b_i x^i = \sum_{i=0}^\infty (a_i + b_i) x^i$$

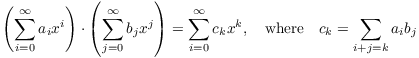
$$\left(\sum_{i=0}^\infty a_i x^i\right) \cdot \left(\sum_{j=0}^\infty b_j x^j\right) = \sum_{i=0}^\infty c_k x^k, \quad {\rm where} \quad c_k = \sum_{i+j=k} a_i b_j$$

These formulas say that you compute sums and products as usual.

Example. ( Polynomial arithmetic) (a) Compute

$$(x^2 + 2 x + 2) + (x^2 + 3) \quad\hbox{and}\quad (x^2 + 2 x + 2) \cdot (x^2 + 3) \quad\hbox{in}\quad \integer_5[x].$$

(b) Compute

$$(2 x^2 + 1) + (4 x^2 + 5) \quad\hbox{and}\quad (3 x + 2) \cdot (2 x + 3) \quad\hbox{in}\quad \integer_6[x].$$

(a)

$$(x^2 + 2 x + 2) + (x^2 + 3) = 2 x^2 + 2 x.$$

$$(x^2 + 2 x + 2) \cdot (x^2 + 3) = x^4 + 2 x^3 + x + 1.\quad\halmos$$

(b)

$$(2 x^2 + 1) + (4 x^2 + 5) = 0.$$

$$(3 x + 2) \cdot (2 x + 3) = 6 x^2 + 13 x + 6 = x.\quad\halmos$$

Let R be an integral domain. Then If $f \in R[x]$ , write $\deg f$ to denote the degree of f. It's easy to show that the degree function satisfies the following properties:

$$\deg (f + g) \le \max (\deg f, \deg g).$$

$$\deg (f \cdot g) = \deg f + \deg g.$$

The verifications amount to writing out the formal sums, with a little attention paid to the case of the zero polynomial. These formulas do work if either f or g is equal to the zero polynomial, provided that $-\infty$ is understood to behave in the obvious ways (e.g. $-\infty + c = -\infty$ for any $c \in \integer$ ).

Example. ( Degrees of polynomials) (a) Give examples of polynomials $f, g \in \real[x]$ such that $\deg (f + g) < \max (\deg f, \deg g).$

(b) Give examples of polynomials $f, g \in \integer_4[x]$ such that $\deg (f \cdot g) \ne \deg f + \deg g$ .

(a)

$$\deg \left[(x^2 + 2) + (-x^2 + 5)\right] = \deg 7 = 0, \quad\hbox{whereas}\quad \max \left[\deg (x^2 + 2), \deg (-x^2 + 5)\right] = 2.$$

This shows that equality might not hold in $\deg (f + g) \le \max (\deg f, \deg g)$ .

(b)

$$\deg (\left[(2 x) \cdot (2 x + 1)\right] = \deg (2 x) = 1, \quad\hbox{but}\quad \deg (2 x) + \deg (2 x + 1) = 1 + 1 = 2.\quad\halmos$$

Proposition. Let F be a field, and let $F[x]$ be the polynomial ring in one variable over F. The units in $F[x]$ are exactly the nonzero elements of F.

Proof. It's clear that the nonzero elements of F are invertible in $F[x]$ , since they're already invertible in F. Conversely, suppose that $f(x) \in F[x]$ is invertible, so $f(x) g(x) = 1$ for some $g(x) \in F[x]$ . Then $\deg f + \deg g = \deg 1 = 0$ , which is impossible unless f and g both have degree 0. In particular, f is a nonzero constant, i.e. an element of F.

Theorem. ( Division Algorithm) Let F be a field, and let $f, g \in F[x]$ . Suppose that $g \ne 0$ . There are unique polynomials $q, r \in F[x]$ such that

$$f(x) = g(x) q(x) + r(x), \quad\hbox{and}\quad \deg r(x) < \deg g(x).$$

Proof. The idea is to imitate the proof of the Division Algorithm for $\integer$ .

Let

$$S = \{f(x) - g(x) q(x) \mid q(x) \in F[x]\}.$$

The set $\{\deg s(x) \mid s(x) \in S\}$ is a subset of the nonnegative integers, and therefore must contain a smallest element by well-ordering. Let $r(x) \in S$ be an element in S of smallest degree, and write

$$r(x) = f(x) - g(x) q(x), \quad\hbox{where}\quad q(x) \in F[x].$$

I need to show that $\deg r(x) < \deg g(x)$ .

If $r(x) = 0$ , then since $g(x) \ne 0$ , I have $\deg g(x) \ge 0 > -\infty = \deg r(x)$ .

Suppose then that $r(x) \ne 0$ . Assume toward a contradiction that $\deg r(x) \ge \deg g(x)$ . Write

$$r(x) = r_n x^n + \cdots + r_1 x + r_0,$$

$$g(x) = g_m x^m + \cdots + g_1 x + g_0.$$

Assume $r_n, g_m \ne 0$ , and $n \ge m$ .

Consider the polynomial

$$r(x) - \dfrac{r_n}{g_m} x^{n - m} g(x) = (r_n x^n + \cdots + r_1 x + r_0) - \left(r_n x^n + \dfrac{r_n}{g_m}x^{n-1}+ \cdots \right).$$

Its degree is less than n, since the n-th degree terms cancel out.

However,

$$r(x) - \dfrac{r_n}{g_m} x^{n - m} g(x) = f(x) - g(x) q(x) - \dfrac{r_n}{g_m} x^{n - m} g(x) = f(x) - g(x) \left(q(x) + \dfrac{r_n}{g_m} x^{n - m} g(x)\right).$$

The latter is an element of S.

I've found an element of S of smaller degree than $r(x)$ , which is a contradiction. It follows that $\deg r(x) < \deg g(x)$ .

Finally, to prove uniqueness, suppose

$$f(x) = g(x) q(x) + r(x) = g(x) q'(x) + r'(x), \quad\hbox{and}\quad \deg r(x), \deg r'(x) < \deg g(x).$$

Rearranging the equation, I get

$$g(x) (q(x) - q'(x)) = r'(x) - r(x).$$

Then

$$\deg (r'(x) - r(x)) = \deg [g(x) (q(x) - q'(x))] = \deg g(x) + \deg (q(x) - q'(x)).$$

But $\deg (r'(x) - r(x)) < \deg g(x)$ . The equation can only hold if

$$\deg (r'(x) - r(x)) = -\infty \quad\hbox{and}\quad \deg (q(x) - q'(x)) = -\infty.$$

This means

$$r'(x) - r(x) = 0 \quad\hbox{and}\quad q(x) - q'(x) = 0.$$

Hence, $r(x) = r'(x)$ and $q(x) = q'(x)$ .

Example. ( Polynomial division) Divide $3 x^4 + 2 x^3 + x + 2$ by $x^2 + 4$ in $\integer_5[x]$ .

Remember as you follow the division that $-4 = 1$ , $-3 = 2$ , and $-2 = 3$ --- I'm doing arithmetic mod 5.

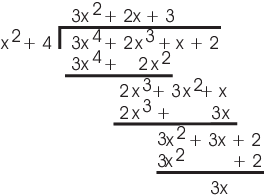
$$\hbox{\epsfysize=1.75 in \epsffile{polynomial-rings1.eps}}$$

If you prefer, you can do long division without writing the powers of x --- i.e. just writing down the coefficients. Here's how it looks:

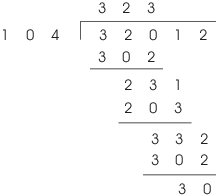
$$\hbox{\epsfysize=1.75 in \epsffile{polynomial-rings2.eps}}$$

Either way, the quotient is $3 x^2 + 2 x + 3$ and the remainder is $3 x$ :

$$3 x^4 + 2 x^3 + x + 2 = (3 x^2 + 2 x + 3)(x^2 + 4) + 3 x.\quad\halmos$$

Definition. Let R be a commutative ring and let $f(x) \in R[x]$ . An element $c \in R$ is a root of $f(x)$ if $f(c) = 0$ .

Note that polynomials are actually formal sums, not functions. However, it is obvious how to plug a number into a polynomial. Specifically, let

$$f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \in R[x].$$

For $c \in R$ , define

$$f(c) = a_n c^n + a_{n-1} c^{n-1} + \cdots + a_1 c + a_0.$$

Observe that a polynomial can be nonzero as a polynomial even if it equals 0 for every input! For example, take $f(x) = x^2 + x \in \integer_2[x]$ is a nonzero polynomial. However, plugging in the two elements of the coefficient ring $\integer_2$ gives

$$f(0) = 0 + 0 = 0 \quad\hbox{and}\quad f(1) = 1 + 1 = 0.$$

Theorem. Let F be a field, and let $f(x) \in F[x]$ , where $\deg f(x) = n \ge 0$ .

(a) ( The Root Theorem) c is a root of $f(x)$ in F if and only if $x - c \mid f(x)$ .

(b) $f(x)$ has at most n roots in F.

Proof. (a) Suppose $f(c) = 0$ . Write

$$f(x) = (x - c) q(x) + r(x), \quad\hbox{where}\quad \deg r(x) < \deg (x - c) = 1.$$

Then $\deg r(x) = 0$ or $\deg r(x) = -\infty$ .

In the first case, r is a nonzero constant. However, this implies that

$$0 = f(c) = 0 \cdot g(c) + r(c) \ne 0.$$

This contradiction shows that $r(x) = 0$ , and $f(x) = (x - c) q(x)$ .

Conversely, if $x - c$ is a factor of $f(x)$ , then $f(x) = (x - c) q(x)$ for some $q(x)$ . Hence,

$$f(c) = q(c) (c - c) = 0.$$

Hence, c is a root of f.

(b) If $c_1, \ldots, c_m$ are the distinct roots of f in F, then

$$(x - c_1) \cdots (x - c_m) \mid f(x).$$

Taking degrees on both sides gives $m \le \deg f(x)$ .

Example. ( Applying the Root Theorem) In $\real[x]$ , show:

(a) $x - 1$ is a factor of $x^{71} - 5 x^{42} + 4$ .

(b) $x - 1$ is a factor of $x^n - 1$ for any $n \ge 1$ .

(a) If $p(x) = x^{71} - 5 x^{42} + 4$ , then $p(1) = 1 - 5 + 4 = 0$ . Hence, 1 is a root of $p(x)$ , and by the Root Theorem $x - 1$ is a factor of $x^{71} - 5 x^{42} + 4$ .

(b) If $p(x) = x^n - 1$ , then $p(1) = 1 - 1 = 0$ . Hence, 1 is a root of $p(x)$ , so $x - 1$ is a factor of $x^n - 1$ by the Root Theorem.

Example. ( Applying the Root Theorem) Prove that $2 x^{51} - 4 x^{49} - 2^{51}$ is divisible by $x - 2$ in $\rational[x]$ .

Plugging in $x = 2$ into $2 x^{51} - 4 x^{49} - 2^{51}$ gives

$$2 \cdot 2^{51} - 4 \cdot 2^{49} - 2^{51} = 2^{52} - 2^{51} - 2^{51} = 2^{52} - 2 \cdot 2^{51} = 2^{52} - 2^{52} = 0.$$

Since $x = 2$ is a root, $x - 2$ is a factor by the Root Theorem.

Remark. If the ground ring isn't a field, it's possible for a polynomial to have more roots than its degree. For example, the quadratic polynomial $(x - 2)(x - 6) \in \integer_{12}[x]$ has roots $x = 0$ , $x = 2$ , $x = 6$ , $x = 8$ . The previous result does not apply, because $\integer_{12}$ is not a field.

Corollary. ( The Remainder Theorem) Let F be a field, $c \in F$ , and let $f(x) \in F[x]$ . When $f(x)$ is divided by $x - c$ , the remainder is $f(c)$ .

Proof. Divide $f(x)$ by $x - c$ :

$$f(x) = q(x) (x - c) + r(x).$$

Since $\deg r(x) < \deg (x - c) = 1$ , it follows that $r(x)$ is a constant. But

$$f(c) = q(c) (c - c) + r(c) = r(c).$$

Therefore, the constant value of $r(x)$ is $r(c) = f(c)$ .

Example. ( Applying the Remainder Theorem) Suppose $p(x) \in \real[x]$ leaves a remainder of 5 when divided by $x - 1$ and a remainder of -1 when divided by $x + 2$ . What is the remainder when $p(x)$ is divided by $(x - 1)(x + 2)$ ?

By the Remainder Theorem,

$$p(1) = 5 \quad\hbox{and}\quad p(-2) = -1.$$

Now divide $p(x)$ by $(x - 1) (x + 2)$ . The remainder $r(x)$ has degree less than $\deg (x - 1) (x + 2) = 2$ , so $r(x) = a x + b$ for some $a, b \in \real$ :

$$p(x) = q(x) (x - 1) (x + 2) + (a x + b).$$

Then

$$5 = p(1) = 0 + (a + b) \quad -1 = p(-2) = 0 + (-2 a + b).$$

Solving the two equations for a and b, I get $a = 2$ and $b = 3$ . Thus, the remainder is $2 x + 3$ .

Definition. Let R be an integral domain.

(a) If $x, y \in R$ , then x divides y if $x z = y$ for some $z \in R$ . Write $x \mid y$ to mean that x divides y.

(b) x and y are associates if $x u = y$ , where u is a unit.

(Recall that a unit in a ring is an element with a multiplicative inverse.)

(c) An element $x \in R$ is irreducible if $x \ne 0$ , x is not a unit, and if $x = y z$ implies either y is a unit or z is a unit.

(d) An element $x \in R$ is prime if $x \ne 0$ , x is not a unit, and $x \mid y z$ implies $x \mid y$ or $x \mid z$ .

Proposition. A nonzero nonconstant polynomial $f(x) \in F[x]$ is irreducible if and only if $f(x) = g(x) h(x)$ implies that either g or h is a constant.

Proof. Suppose $f(x)$ is irreducible and $f(x) = g(x) h(x)$ . Then one of $g(x)$ , $h(x)$ is a unit. But we showed earlier that the units in $F[x]$ are the constant polynomials.

Suppose that $f(x)$ is a nonzero nonconstant polynomial, and $f(x) = g(x) h(x)$ implies that either g or h is a constant.

Since f is nonconstant, it's not a unit. Note that if $f(x) = g(x) = h(x)$ , then $g, h \ne 0$ , since $f \ne $ .

Therefore, the condition that $f(x) = g(x) h(x)$ implies that either g or h is a constant means that $f(x) = g(x) h(x)$ implies that either $g(x)$ or $h(x)$ is a unit --- again, since the nonzero constant polynomials are the units in $F[x]$ . This is what it means for f to be irreducible.

Example. Show that $x^2 + 1$ is irreducible in $\real[x]$ but not in $\complex[x]$ .

$x^2 + 1$ has no real roots, so by the Root Theorem it has no linear factors. Hence, it's irreducibile in $\real[x]$ .

However, $x^2 + 1 = (x + i)(x - i)$ in $\complex[x]$ .

Corollary. Let F be a field. A polynomial of degree 2 or 3 in $F[x]$ is irreducible if and only if it has no roots in F.

Proof. Suppose $f \in F[x]$ has degree 2 or 3.

If f is not irreducible, then $f(x) = g(x) h(x)$ , where neither g nor h is constant. Now $\deg g \ge 1$ and $\deg h \ge 1$ , and

$$\deg g + \deg h = \deg f = 2 \quad\hbox{or}\quad 3.$$

This is only possible if at least one of g or h has degree 1. This means that at least one of g or h is a linear factor $a x + b$ , and must therefore have a root in F. Since $f(x) = g(x) h(x)$ , it follows that f has a root in F as well.

Conversely, if f has a root c in F, then $x - c$ is a factor of f by the Root Theorem. Since f has degree 2 or 3, $x - c$ is a proper factor, and f is not irreducible.

Remark. The result is false for polynomials of degree 4 or higher. For example, $(x^2 + 1)^2$ has no roots in $\real$ , but it is not irreducible over $\real$ .

Example. ( Checking for irreducibility of a quadratic or cubic) Show that $x^3 + x + 1 \in \integer_5[x]$ is irreducible.

Since this is a cubic polynomial, I only need to see whether it has any roots.

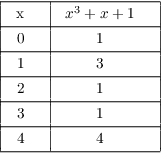
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & x & & $x^3 + x + 1$ & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 0 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 1 & & 3 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 2 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 4 & & 4 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Since $x^3 + x + 1$ has no roots in $\integer_5$ , it's irreducible.

Proposition. In an integral domain, primes are irreducible.

Proof. Let x be prime. I must show x is irreducible. Suppose $x = y z$ . I must show either y or z is a unit.

$x = y z$ , so obviously $x \mid y z$ . Thus, $x \mid y$ or $x \mid z$ . Without loss of generality, suppose $x \mid y$ .

Write $x w = y$ . Then $x = y z = x w z$ , and since $x \ne 0$ (primes are nonzero) and we're in a domain, $1 = w z$ . Therefore, z is a unit, and x is irreducible.

Definition. Let R be an integral domain, and let $x, y \in R$ . $d \in R$ is a greatest common divisor of x and y if:

(a) $d \mid x$ and $d \mid y$ .

(b) If $d'\mid x$ and $d' \mid y$ , then $d' \mid d$ .

The definition says "a" greatest common divisor, rather than "the" greatest common divisor, because greatest common divisors are only unique up to multiplication by units.

The definition above is the right one if you're dealing with an arbitrary integral domain. However, if your ring is a polynomial ring, it's nice to single out a "special" greatest common divisor and call it the greatest common divisor.

Definition. A monic polynomial is a polynomial whose leading coefficient is 1.

For example, here are some monic polynomials over $\rational$ :

$$x^3 - 3 x + 5, \quad x^{100} - \dfrac{2}{3}x^{17}, \quad x + 42.$$

Definition. Let F be a field, let $F[x]$ be the ring of polynomials with coefficients in F, and let $f, g \in F[x]$ , where f and g are not both zero. The greatest common divisor of f and g is the monic polynomial which is a greatest common divisor of f and g (in the integral domain sense).

Example. ( Polynomial greatest common divisors) Find the greatest common divisor of $x^2 - 4$ and $x^2 - x - 2$ in $\rational[x]$ .

$x - 2$ is a greatest common divisor of $x^2 - 4$ and $x^2 - x - 2$ :

$$x^2 - 4 = 1\cdot(x^2 - x - 2) + (x - 2)$$

$$x^2 - x - 2 = (x + 1)(x - 2) + 0$$

Notice that any nonzero constant multiple of $x - 2$ is also a greatest common divisor of $x^2 - 4$ and $x^2 - x - 2$ (in the integral domain sense): For example, $\dfrac{1}{100} (x - 2)$ works. This makes sense, because the units in $\rational[x]$ are the nonzero elements of $\rational$ . But by convention, I'll refer to $x - 2$ --- the monic greatest common divisor --- as the greatest common divisor of $x^2 - 4$ and $x^2 - x - 2$ .

The preceding definition assumes there is a greatest common divisor for two polynomials in $F[x]$ . In fact, the greatest common divisor of two polynomials exists --- provided that both polynomials aren't 0 --- and the proof is essentially the same as the proof for greatest common divisors of integers.

In both cases, the idea is to use the Division Algorithm repeatedly until you obtain a remainder of 0. This must happen in the polynomial case, because the Division Algorithm for polynomials specifies that the remainder has strictly smaller degree than the divisor.

Just as in the case of the integers, each use of the Division Algorithm does not change the greatest common divisor. So the last pair has the same greatest common divisor as the first pair --- but the last pair consists of 0 and the last nonzero remainder, so the last nonzero remainder is the greatest common divisor.

This process is called the Euclidean algorithm, just as in the case of the integers.

Let h and $h'$ be two greatest common divisors of f and g. By definition, $h \mid h'$ and $h' \mid h$ . From this, it follows that h and $h'$ have the same degree, and are constant multiples of one another. If h and $h'$ are both monic --- i.e. both have leading coefficient 1 --- this is only possible if they're equal. So there is a unique monic greatest common divisor for any two polynomials.

Finally, the same proofs that I gave for the integers show that you can write the greatest common divisor of two polynomials as a linear combination of the two polynomials. You can use the Extended Euclidean Algorithm that you learned for integers to find a linear combination. To summarize:

Theorem. Let F be a field, $f, g \in F[x]$ , f and g not both 0.

(a) f and g have a unique (monic) greatest common divisor.

(b) There exist polynomials $u, v \in F[x]$ such that

$$(f(x), g(x)) = u(x) f(x) + v(x) g(x).\quad\halmos$$

Example. ( Applying the Extended Euclidean Algorithm) Find the greatest common divisor of $x^4 - x^3 + x^2 - 1$ and $x^3 - x^2 + 3 x - 3$ in $\real[x]$ and express the greatest common divisor as a linear combination of $x^3 + 1$ and $x^2 + 4 x + 3$ with coefficients in $\real[x]$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^4 - x^3 + x^2 - 1$ & & - & & $\dfrac{1}{2}x^2 - \dfrac{1}{4}x + 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^3 - x^2 + 3 x - 3$ & & x & & $-\dfrac{1}{2}x - \dfrac{1}{4}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $-2 x^2 + 3 x - 1$ & & $-\dfrac{1}{2}x - \dfrac{1}{4}$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $\dfrac{13}{4}x - \dfrac{13}{4}$ & & $-\dfrac{8}{13}x + \dfrac{4}{13}$ & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The greatest common divisor is $\dfrac{13}{4} x - \dfrac{13}{4}$ . The greatest common divisor is only determined up to multiplying by a unit, so multiplying by $\dfrac{4}{13}$ gives the monic greatest common divisor $x - 1$ .

You can check that

$$-\left(-\dfrac{1}{2} x - \dfrac{1}{4}\right) \left(x^4 - x^3 + x^2 - 1\right) + \left(-\dfrac{1}{2} x^2 - \dfrac{1}{4} x + 1\right) \left(x^3 - x^2 + 3 x - 3\right) = \dfrac{13}{4} x - \dfrac{13}{4}.\quad\halmos$$

Example. ( Applying the Extended Euclidean Algorithm) Find the greatest common divisor of $x^3 + 1$ and $x^2 + 4 x + 3$ in $\integer_5[x]$ and express the greatest common divisor as a linear combination of $x^3 + 1$ and $x^2 + 4 x + 3$ with coefficients in $\integer_5[x]$ .

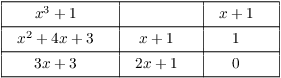
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^3 + 1$ & & & & $x + 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^2 + 4 x + 3$ & & $x + 1$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $3 x + 3$ & & $2 x + 1$ & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The greatest common divisor is $3 x + 3$ , and

$$3 x + 3 = -(x + 1) \cdot (x^2 + 4 x + 3) + 1 \cdot (x^3 + 1) = 4 (x + 1) \cdot (x^2 + 4 x + 3) + 1 \cdot (x^3 + 1).$$

The greatest common divisor is only determined up to multiplying by a unit. So, for example, I can multiply the last equation by 2 to get

$$x + 1 = (3 x + 3) \cdot (x^2 + 4 x + 3) + 2 \cdot (x^3 + 1).\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga