Prime Numbers

Definition. An integer n greater than 1 is prime if the only positive divisors of n are 1 and n.

A positive integer n which has a positive divisor other than 1 or n is composite.

People are often puzzled by the fact that 1 is not considered to be prime. Excluding 1 is a convention which makes other things more convenient (such as the statement of the Fundamental Theorem of Arithmetic).

Example. ( Small prime numbers and composite numbers) List the prime and composite numbers in the set $\{1, 2, \ldots 10\}$ .

Primes:

$$2, \quad 3, \quad 5, \quad 7, \quad \ldots.$$

Composite numbers:

$$4, \quad, 6, \quad, 8, \quad 9.\quad\halmos$$

Lemma. Every integer greater than 1 is divisible by a prime number.

Proof. The result is true for 2, since 2 is prime and $2 \mid 2$ .

Let $n > 2$ , and suppose the result is true for all positive integers greater than 1 and less than n. I want to show that n is divisible by a prime number.

If n is prime, then n is divisible by a prime number --- itself.

If n isn't prime, then it's composite. Therefore, n has a positive divisor m such that $m \ne 1$ and $m \ne n$ . Plainly, m can't be larger than n, so $1 < m < n$ . By induction, m is divisible by some prime number p. Now $p \mid m$ and $m \mid n$ , so $p \mid n$ . This proves that n is divisible by a prime number, and completes the induction step. Hence, then result is true for all integers greater than 1 by induction.

You've probably seen the classical proof of the next result, which goes back to Euclid. Well, in case you haven't (or you've forgotten), here it is.

Theorem. There are infinitely many prime numbers.

Proof. Suppose on the contrary that there were only finitely many primes $p_1$ , $p_2$ , ... $p_n$ . Every integer greater than 1 is either prime --- so it's one of the p's --- or it's composite, and by the preceding lemma, divisible by one of the p's.

Consider the number $m = p_1 p_2\cdots p_n + 1$ . m leaves a remainder of 1 when it's divided by $p_1$ , $p_2$ , ... $p_n$ . Therefore, it's not composite. But it can't be one of the primes, since it's larger than all of the p's. This is a contradiction, so there must be infinitely many primes.

Prime numbers used to be a mathematical curiosity. In the last few decades, they've found important applications --- for example, to the field of cryptography. But there's still a lot to be curious about.

Question. ( Goldbach's conjecture) Can every even integer greater than 4 be expressed as the sum of two primes?

Goldbach's conjecture has been verified for even numbers up to around $10^{14}$ .

Question. ( Twin Prime conjecture) Twin primes are prime number which are 2 units apart (such as 5 and 7). Are there infinitely many twin primes?

The largest known twin primes as of this writing are $2996863034895 \cdot 2^{1290000} \pm 1$ . They have $388\,342$ digits.

Question. A Mersenne prime is a prime number of the form $2^n - 1$ , where n is a positive integer (such as $31 = 2^5 - 1$ ). Are there infinitely many Mersenne primes?

The Mersenne prime $2^{77\,232\,917}-1$ is the largest known prime number as of January, 2018. It was discovered on December 26, 2017 by Jonathan Pace as a part of GIMPS (the Great Internet Mersenne Prime Search: www.mersenne.org). It has $23\,249\,425$ decimal digits.

Lemma. Suppose p is prime. Then p is relatively prime to a if and only if $p \notdiv a$ .

Proof. Suppose that $(p, a) = 1$ . I want to show that $p \notdiv a$ . Suppose on the contrary that $p \mid a$ . Since $p \mid p$ , p is a common divisor of p and a. Therefore, $p \mid (p, a) = 1$ . This is a contradiction, since p is prime.

Conversely, suppose $p \notdiv a$ . I want to show that $(p, a) = 1$ .

Now $(p, a) \mid p$ , and the only positive numbers that divide p and 1 and p. Therefore, $(p, a) = 1$ or $(p, a) = p$ .

Suppose $(p, a) = p$ . Then $p = (p, a) \mid a$ , which contradicts my assumption that $p \notdiv a$ .

Therefore, $(p, a) \ne p$ , so $(p, a) = 1$ .

Theorem. ( Euclid's lemma) Let p be prime, and suppose $p \mid ab$ . Then $p \mid a$ or $p \mid b$ .

Proof. Let p be prime, and suppose $p \mid a b$ . To show that $p \mid a$ or $p \mid b$ , I'll assume that $p \notdiv a$ and prove that $p \mid b$ .

Since $p \notdiv a$ , the preceding result says that $(p, a) = 1$ . Therefore, I can find integers m and n such that

$$m p + n a = 1.$$

Multiply by b:

$$m p b + n a b = b.$$

$p \mid m p b$ , and by assumption $p \mid a b$ , so $p \mid n a b$ . Therefore, $p \mid m p b + n a b = b$ , which is what I wanted to prove.

Remarks. 1. There is a general version of Euclid's lemma: If p is prime and $p \mid a_1 a_2\cdots a_n$ , then p divides at least one of the a's.

2. If p and q are primes and $p \mid q$ , then $p = q$ . (Only 1 and q divide q, and p isn't 1, so it must be q.) Using this fact and the general version of Euclid's lemma, you can show that if p and q are primes, $n \ge 1$ , and $p \mid q^n$ , then $p = q$ .

Example. ( Using Euclid's lemma to prove a divisibility statement) Prove that if p is prime and $p \mid a^2$ , then $p \mid a$ .

Since $p \mid a^2 = a \cdot a$ , Euclid's lemma implies that $p \mid a$ or $p \mid a$ . Hence, $p \mid a$ .

Try writing out the induction proof that shows that if p is prime, $n > 2$ , and $p \mid a^n$ , then $p \mid a$ .

Example. ( A problem on primes and squares) For what prime numbers p is $13 p + 1$ a perfect square?

Suppose $13 p + 1 = x^2$ , where $x \in \integer$ . First, if $x = 0$ , then $13 p + 1 = 0$ , so $13 p = -1$ . Since p is prime, it is positive, and this is a contradiction.

Therefore, $x \ne 0$ , and I may assume without loss of generality that x is positive: If x is negative, then $-x$ is positive, and $13 p + 1 = (-x)^2$ holds.

Thus, I'm now assuming that $x > 0$ .

I'll rule out another special case: If $x = 1$ , I have $13 p + 1 = 1$ , or $13 p = 0$ . Since p is prime, $p > 1$ , so this is impossible.

Now I can assume that $x > 1$ . This means that $x - 1 > 0$ . Moreover, $x + 1 > x - 1$ , so $x + 1 > 0$ . In other words, $x - 1$ and $x + 1$ are positive numbers.

Now I'll proceed with the main part of the proof. I have

$$13 p = x^2 - 1 = (x - 1)(x + 1).$$

This says that $x - 1$ and $x + 1$ are positive factors of $13 p$ . Since 13 and p are prime, the only positive factors of $13 p$ are 1, p, 13, and $13 p$ . There are four cases.

Suppose that $13 = x - 1$ and $p = x + 1$ . The first equation gives $x = 14$ , so $p = 15$ . This contradicts the fact that p is prime.

Suppose that $13 = x + 1$ and $p = x - 1$ . The first equation gives $x = 12$ , so $p = 11$ . 11 is prime, and $13\cdot 11 + 1 = 144 = 12^2$ .

Suppose that $13 p = x - 1$ and $1 = x + 1$ . The second equation gives $x = 0$ , but I'm assuming $x > 0$ . This contradiction rules out this case.

Finally, suppose that $1 = x - 1$ and $13 p = x + 1$ . The first equation gives $x = 2$ , which yields $13 p = 3$ in the second equation. But p is prime, so $p > 1$ , and $13 p > 13$ . Thus, $13 p$ can't equal 3, and this contradiction rules out this case.

Thus, the only prime p for which $13 p + 1$ is a perfect square is $p = 11$ .

Theorem. ( The Fundamental Theorem of Arithmetic) Let n be an integer, $n > 1$ . Then n can be written as a product of prime numbers, and this product is unique up to the order of the factors.

"Up to the order of the factors" means that $2\cdot 3$ and $3\cdot 2$ are considered to be "the same" factorization of 6.

Proof. First, I'll show that every integer greater than 1 can be factored into a product of primes.

I'll use induction. Start with $n = 2$ ; this is prime, so the result holds for $n = 2$ .

Next, let $n > 2$ , and suppose every integer greater than 1 and less than n can be factored into a product of primes. If n is prime, then n is a product of primes (namely, itself), and I'm done.

Otherwise, n is composite. This implies that there are integers a and b with $1 < a, b < n$ such that $n = ab$ . Since a and b are between 1 and n, each of them can be factored into a product of primes, by the induction hypothesis. Then $n = ab$ shows that the same is true of n.

By induction, every integer greater than 1 can be factored into a product of primes.

Next, I want to show that the prime factorization of a positive integer is unique, up to the order of the factors.

Suppose I have two prime factorizations of the same number:

$$p_1^{r_1}p_2^{r_2}\cdots p_m^{r_m} = q_1^{s_1}q_2^{s_2}\cdots q_n^{s_n}.$$

Thus, the p's and q's are primes, all the p's are distinct and all the q's are distinct (but some p's may be q's, and vice versa), and all the exponents are positive.

Start with $p_1$ . It's prime, and it divides the left side, so it divides the right side:

$$p_1 \mid q_1^{s_1}q_2^{s_2}\cdots q_n^{s_n}.$$

By the general version of Euclid's lemma, $p_1$ must divide some $q_k^{s^k}$ . I can assume $p_1 \mid q_1^{s^1}$ (because if $p_1$ divided one of the other q-powers, I could stop and rename everything so the one it divides is $q_1^{s^1}$ ). By the second remark following Euclid's lemma, this implies $p_1 = q_1$ .

Now the equation looks like this:

$$p_1^{r_1}p_2^{r_2}\cdots p_m^{r_m} = p_1^{s_1}q_2^{s_2}\cdots q_n^{s_n}.$$

I cancel as many $p_1$ 's off both sides as I can. Suppose I wind up with some left-over $p_1$ 's on the right:

$$p_2^{r_2}\cdots p_m^{r_m} = p_1^tq_2^{s_2}\cdots q_n^{s_n}.$$

Now I repeat the divisibility argument. $p_1$ divides the right side, so it divides the left side $p_2^{r_2}\cdots p_m^{r_m}$ . As before, this means that $p_1$ is one of $p_2$ , ..., $p_m$ . This is a contradiction, because I assumed at the start that the p's were distinct.

This means that there can't be any left-over $p_1$ 's on the right, and a similar argument shows that there can't be any left-over $p_1$ 's on the left. Hence, all the $p_1$ 's must have cancelled, and I have

$$p_2^{r_2}\cdots p_m^{r_m} = q_2^{s_2}\cdots q_n^{s_n}.$$

I continue in this way, matching up prime powers on the two sides. Eventually, everything must match up (just as $p_1^{r_1}$ and $q_1^{s_1}$ did), which shows that the two original factorizations were identical.

This proves that the prime factorization of an integer is unique, up to order.

Example. ( Factoring a number into primes) Apply the Fundamental Theorem of Arithmetic to 3768.

I can do this by trial division:

$$3768 = 2 \cdot 1884 = 2 \cdot 2 \cdot 942 = 2 \cdot 2 \cdot 2 \cdot 471 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 157.$$

(157 is prime, so that's where I stop.) Therefore, $3768 = 2^3 \cdot 3 \cdot 157$ .

Trial division is not a useful way of factoring numbers once they get too large. In general factoring big integers is a hard problem involving many sophisticated methods.

Definition. If m and n are positive integers, the least common multiple of m and n is the smallest positive integer which is divisible by both m and n. The least common multiple of m and n is denoted $[m, n]$ .

Example. ( Least common multiples) (a) Compute $[24, 16]$ .

(b) Suppose p and q are distinct primes. Compute $[p^2 q^5, p^4, q^3]$ .

(a) $[24, 16] = 48$ , since $24 \mid 48$ and $16 \mid 48$ , and no smaller positive integer is divisible by both 24 and 16.

(b) The least common multiple of $p^2$ and $p^4$ is $p^4$ , since it's clearly the smallest power of p divisible by both $p^2$ and $p^4$ . You can see that for two positive powers of a prime, their least common multiple is the largest of the two powers. So for $q^5$ and $q^3$ , the least common multiple is $q^5$ . Hence, $[p^2 q^5, p^4, q^3] = p^4 q^5$ .

The prime factorization of a number provides a way of visualizing greatest common divisors and least common multiples.

Example. ( Finding greatest common divisors and least common multiples using prime factorizations) Represent the greatest common divisor and least common multiple of 120 and 280 by drawing a Venn diagram involving their prime factorizations.

Note that

$$120 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \quad\hbox{and}\quad 280 = 2 \cdot 2 \cdot 2 \cdot 5 \cdot 7.$$

Arrange the prime factors of the two numbers in a Venn diagram:

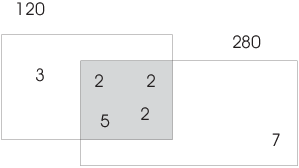
$$\hbox{\epsfysize=1.5 in \epsffile{prime-numbers-1.eps}}$$

The factors 2, 2, 2, and 5 are common to the two numbers. They go in the intersection (shaded), and their product $2 \cdot 2 \cdot 2 \cdot 5 = 40$ is equal to the greatest common divisor $(120, 280)$ .

The least common multiple $[120, 280]$ is the product of all the numbers in the diagram (counted once each):

$$[120, 280] = 3 \cdot (2 \cdot 2 \cdot 2 \cdot 5)\cdot 7 = 1680.$$

Note that if you multiply 120 and 280, this counts the primes in the intersection --- whose product is $(120, 280)$ --- twice, whereas $[120, 280]$ counts the primes in the intersection once. It follows that

$$120 \cdot 280 = [120, 280] \cdot (120, 280).$$

This is true in general: If m and n are positive integers, then $m n = [m,n]\cdot (m,n)$ . The argument above isn't a proof, but it makes the result plausible.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga