Quotient Rings of Polynomial Rings

In this section, I'll look at quotient rings of polynomial rings.

Let F be a field, and suppose $p(x) \in F[x]$ . $\langle p(x)\rangle$ is the set of all multiples (by polynomials) of $p(x)$ , the (principal) ideal generated by $p(x)$ . When you form the quotient ring $\dfrac{F[x]}{\langle p(x)\rangle}$ , it is as if you've set multiples of $p(x)$ equal to 0.

If $a(x) \in F[x]$ , then $a(x) + \langle p(x)\rangle$ is the coset of $\langle p(x)\rangle$ represented by $a(x)$ .

Define $a(x) = b(x) \mod{p(x)}$ ($a(x)$ is congruent to $b(x)$ mod $p(x)$ ) to mean that

$$p(x) \mid a(x) - b(x).$$

In words, this means that $a(x)$ and $b(x)$ are congruent mod $p(x)$ if they differ by a multiple of $p(x)$ . In equation form, this says $a(x) - b(x) = k(x) \cdot p(x)$ for some $k(x) \in F[x]$ , or $a(x) = b(x) + k(x) \cdot p(x)$ for some $k(x) \in F[x]$ .

Lemma. Let R be a commutative ring, and suppose $a(x), b(x), p(x) \in R[x]$ . Then $a(x) = b(x) \mod{p(x)}$ if and only if $a(x) + \langle p(x) \rangle = b(x) + \langle p(x) \rangle$ .

Proof. Suppose $a(x) = b(x) \mod{p(x)}$ . Then $a(x) = b(x) + k(x) \cdot p(x)$ for some $k(x) \in R[x]$ . Hence,

$$a(x) + \langle p(x) \rangle = b(x) + k(x) \cdot p(x) + \langle p(x) \rangle = b(x) + \langle p(x) \rangle.$$

Conversely, suppose $a(x) + \langle p(x) \rangle = b(x) + \langle p(x) \rangle$ . Then

$$a(x) \in a(x) + \langle p(x) \rangle = b(x) + \langle p(x) \rangle.$$

Hence,

$$a(x) = b(x) + k(x) \cdot p(x) \quad\hbox{for some}\quad k(x) \in R[x].$$

This means that $a(x) = b(x) \mod{p(x)}$ .

Depending on the situation, I may write $a(x) = b(x) \mod{p(x)}$ or $a(x) + \langle p(x) \rangle = b(x) + \langle p(x) \rangle$ .

Example. ( A quotient ring of the rational polynomial ring) Take $p(x) = x - 2$ in $\rational[x]$ . Then two polynomials are congruent mod $x - 2$ if they differ by a multiple of $x - 2$ .

(a) Show that $2 x^2 + 3 x + 5 = x^2 + 4 x + 7 \mod{x - 2}$ .

(b) Find a rational number r such that $x^3 - 4 x^2 + x + 11 = r \mod{x - 2}$ .

(c) Prove that $\dfrac{\rational[x]}{\langle x - 2\rangle} \approx \rational$ .

(a)

$$(2 x^2 + 3 x + 5) - (x^2 + 4 x + 7) = x^2 - x - 2 = (x + 1)(x - 2), \quad\hbox{so}\quad 2 x^2 + 3 x + 5 = x^2 + 4 x + 7 \mod{x - 2}.\quad\halmos$$

(b) By the Remainder Theorem, when $f(x) = x^3 - 4 x^2 + x + 11$ is divided by $x - 2$ , the remainder is

$$f(2) = 2^3 - 4 \cdot 2^2 + 2 + 11 = 5.$$

Thus,

$$\eqalign{ x^3 - 4 x^2 + x + 11 & = (x - 2) q(x) + 5 \cr x^3 - 4 x^2 + x + 11 & = 5 \mod{x - 2} \cr} \quad\halmos$$

(c) I'll use the First Isomorphism Theorem. Define $\phi: \rational[x] \to \rational$ by

$$\phi\left(f(x)\right) = f(2).$$

That is, $\phi$ evaluates a polynomial at $x = 2$ . Note that

$$\phi\left(f(x) + g(x)\right) = f(2) + g(2) = \phi\left(f(x)\right) + \phi\left(g(x)\right) \quad\hbox{and}\quad \phi\left(f(x) g(x)\right) = f(2) g(2) = \phi\left(f(x)\right)\phi\left(g(x)\right),$$

It follows that $\phi$ is a ring map.

I claim that $\ker \phi = \langle x - 2\rangle$ . Now $f(x) \in \ker \phi$ if and only if

$$f(2) = \phi\left(f(x)\right) = 0.$$

That is, $f(x) \in \ker \phi$ if and only if 2 is a root of f. By the Root Theorem, this is equivalent to $x - 2 \mid f(x)$ , which is equivalent to $f(x) \in \langle x - 2\rangle$ .

Next, I'll show that $\phi$ is surjective. Let $q \in \rational$ . I can think of q as a constant polynomial, and doing so, $\phi(q) = q$ . Therefore, $\phi$ is surjective.

Using these results,

$$\dfrac{\rational[x]}{\langle x - 2\rangle} = \dfrac{\rational[x]}{\ker \phi} \approx \im \phi = \rational.$$

The first equality follows from the fact that $\langle x - 2\rangle = \ker \phi$ . The isomorphism follows from the First Isomorphism Theorem. The second equality follows from the fact that $\phi$ is surjective.

In the last example, $\dfrac{F[x]}{\langle p(x) \rangle}$ was a field. The next result says that this is the case exactly when $p(x)$ is irreducible.

Theorem. $\dfrac{F[x]}{\langle p(x) \rangle}$ is a field if and only if $p(x)$ is irreducible.

Proof. Since $F[x]$ is a commutative ring with identity, so is $\dfrac{F[x]}{\langle p(x) \rangle}$ .

Suppose $p(x)$ is irreducible. I need to show that $\dfrac{F[x]}{\langle p(x) \rangle}$ is a field. I need to show that nonzero elements are invertible.

Take a nonzero element of $\dfrac{F[x]}{\langle p(x) \rangle}$ --- say $a(x) + \langle p(x) \rangle$ , for $a(x) \in F[x]$ . What does it mean for $a(x) + \langle p(x) \rangle$ to be nonzero? It means that $a(x) \notin \langle p(x) \rangle$ , so $p(x) \notdiv a(x)$ .

Now what is the greatest common divisor of $a(x)$ and $p(x)$ ? Well, $(a(x), p(x)) \mid p(x)$ , but $p(x)$ is irreducible --- its only factors are units and unit multiples of $p(x)$ .

Suppose $(a(x), p(x)) = k \cdot p(x)$ , where $k \in F$ and $k \ne 0$ . Then $k \cdot p(x) \mid a(x)$ , i.e. $k\cdot p(x) b(x) = a(x)$ for some $b(x)$ . But then $p(x)[k \cdot b(x)] = a(x)$ shows that $p(x) \mid a(x)$ , contrary to assumption.

The only other possibility is that $(a(x), p(x)) = k$ , where $k \in F$ and $k \ne 0$ . So I can find polynomials $m(x)$ , $n(x)$ , such that

$$a(x) m(x) + p(x) n(x) = k.$$

Then

$$a(x) \cdot \left(\dfrac{1}{k} m(x)\right) + p(x) \cdot \left(\dfrac{1}{k} n(x)\right) = 1.$$

Hence,

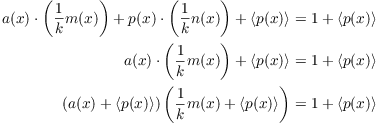
$$\eqalign{ a(x) \cdot \left(\dfrac{1}{k} m(x)\right) + p(x) \cdot \left(\dfrac{1}{k} n(x)\right) + \langle p(x) \rangle & = 1 + \langle p(x) \rangle \cr a(x) \cdot \left(\dfrac{1}{k} m(x)\right) + \langle p(x) \rangle & = 1 + \langle p(x) \rangle \cr \left(a(x) + \langle p(x) \rangle\right) \left(\dfrac{1}{k} m(x) + \langle p(x) \rangle\right) & = 1 + \langle p(x) \rangle \cr}$$

This shows that $\dfrac{1}{k} m(x) + \langle p(x) \rangle$ is the multiplicative inverse of $a(x) + \langle p(x) \rangle$ . Therefore, $a(x) + \langle p(x) \rangle$ is invertible, and $\dfrac{F[x]}{\langle p(x) \rangle}$ is a field.

Going the other way, suppose that $p(x)$ is not irreducible. Then I can find polynomials $c(x)$ , $d(x)$ such that $p(x) = c(x) d(x)$ , where $c(x)$ and $d(x)$ both have smaller degree than $p(x)$ .

Because $c(x)$ and $d(x)$ have smaller degree than $p(x)$ , they're not divisible by $p(x)$ . In particular,

$$c(x) + \langle p(x) \rangle \ne 0 \quad\hbox{and}\quad d(x) + \langle p(x) \rangle \ne 0.$$

But $p(x) = c(x) d(x)$ gives

$$\eqalign{ p(x) + \langle p(x) \rangle & = c(x) d(x) + \langle p(x) \rangle \cr 0 & = \left(c(x) + \langle p(x) \rangle\right)\left(d(x) + \langle p(x) \rangle\right) \cr}$$

This shows that $\dfrac{F[x]}{\langle p(x) \rangle}$ has zero divisors. Therefore, it's not an integral domain --- and since fields are integral domains, it can't be a field, either.

Example. ( A quotient ring which is not an integral domain) Prove that $\dfrac{\rational[x]}{\langle x^2 - 1\rangle}$ is not an integral domain by exhibiting a pair of zero divisors.

$(x - 1) + \langle x^2 - 1\rangle$ and $(x + 1) + \langle x^2 - 1\rangle$ are zero divisors, because

$$(x - 1)(x + 1) = x^2 - 1 = 0 \mod {x^2 - 1}.\quad\halmos$$

Example. ( A quotient ring which is a field) (a) Show that $\dfrac{\rational[x]}{\langle x^2 + 2 x + 2\rangle}$ is a field.

(b) Find the inverse of $(x^3 + 1) + \langle x^2 + 2 x + 2 \rangle$ in $\dfrac{\rational[x]}{\langle x^2 + 2 x + 2\rangle}$ .

(a) Since $x^2 + 2 x + 2 = (x + 1)^2 + 1 > 0$ for all $x \in \rational$ , it follows that $x^2 + 2 x + 2$ has no rational roots. Hence, it's irreducible, and the quotient ring is a field.

(b) Apply the Extended Euclidean algorithm to $x^3 + 1$ and $x^2 + 2 x + 2$ :

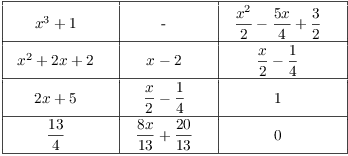
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^3 + 1$ & & - & & $\dfrac{x^2}{2} - \dfrac{5 x}{4} + \dfrac{3}{2}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^2 + 2 x + 2$ & & $x - 2$ & & $\dfrac{x}{2} - \dfrac{1}{4}$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $2 x + 5$ & & $\dfrac{x}{2} - \dfrac{1}{4}$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $\dfrac{13}{4}$ & & $\dfrac{8 x}{13} + \dfrac{20}{13}$ & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Therefore,

$$\dfrac{13}{4} = \left(\dfrac{x^2}{2} - \dfrac{5 x}{4} + \dfrac{3}{2}\right)(x^2 + 2 x + 2) - \left(\dfrac{x}{2} - \dfrac{1}{4}\right)(x^3 + 1).$$

Hence,

$$1 = \dfrac{4}{13} \left(\dfrac{x^2}{2} - \dfrac{5 x}{4} + \dfrac{3}{2}\right)(x^2 + 2 x + 2) - \dfrac{4}{13} \left(\dfrac{x}{2} - \dfrac{1}{4}\right)(x^3 + 1).$$

Reducing mod $x^2 + 2 x + 2$ , I get

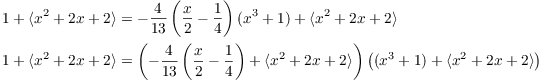
$$\eqalign{ 1 + \langle x^2 + 2 x + 2 \rangle & = -\dfrac{4}{13}\left(\dfrac{x}{2} - \dfrac{1}{4}\right)(x^3 + 1) + \langle x^2 + 2 x + 2 \rangle \cr 1 + \langle x^2 + 2 x + 2 \rangle & = \left(-\dfrac{4}{13}\left(\dfrac{x}{2} - \dfrac{1}{4}\right) + \langle x^2 + 2 x + 2 \rangle\right) \left((x^3 + 1) + \langle x^2 + 2 x + 2 \rangle\right) \cr}$$

Thus, $-\dfrac{4}{13}\left(\dfrac{x}{2} - \dfrac{1}{4}\right) + \langle x^2 + 2 x + 2 \rangle$ is the inverse of $(x^3 + 1) + \langle x^2 + 2 x + 2 \rangle$ .

Example. ( A field with 4 elements) (a) Prove that $\dfrac{\integer_2[x]}{\langle x^2 + x + 1\rangle}$ is a field.

(b) Find $a x + b \in \integer_2[x]$ so that

$$(x^4 + x^3 + 1) + \langle x^2 + x + 1\rangle = (a x + b) + \langle x^2 + x + 1\rangle.$$

(c) Construct addition and multiplication tables for $\dfrac{\integer_2[x]}{\langle x^2 + x + 1\rangle}$ .

(a) Let $f(x) = x^2 + x + 1$ . Then $f(0) = 1$ and $f(1) = 1$ . Since f has no roots in $\integer_2$ , it's irreducible. Hence, $\dfrac{\integer_2[x]}{\langle x^2 + x + 1\rangle}$ is a field.

(b) By the Division Algorithm,

$$x^4 + x^3 + 1 = (x^2 + x + 1)(x^2 + 1) + x.$$

This equation says that $x^4 + x^3 + 1$ and x differ by a multiple of $x^2 + x + 1$ , so they represent the same coset mod $x^2 + x + 1$ .

Therefore,

$$(x^4 + x^3 + 1) + \langle x^2 + x + 1\rangle = x + \langle x^2 + x + 1\rangle.\quad\halmos$$

(c) By the Division Algorithm, if $f(x) \in \integer_2[x]$ , then

$$f(x) = (x^2 + x + 1) q(x) + (a x + b), \quad\hbox{where}\quad a, b \in \integer_2.$$

There are two possibilities for a and two for b, a total of 4. It follows that $\dfrac{\integer_2[x]}{\langle x^2 + x + 1\rangle}$ is a field with 4 elements. The elements are

$$0 + \langle x^2 + x + 1 \rangle, 1 + \langle x^2 + x + 1 \rangle, x + \langle x^2 + x + 1 \rangle, (x + 1) + \langle x^2 + x + 1 \rangle.$$

Here are the addition and multiplication tables for $\dfrac{\integer_2[x]}{\langle x^2 + x + 1\rangle}$ :

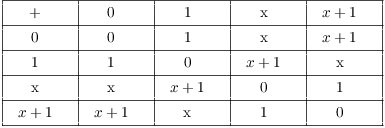
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & x & & $x + 1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & x & & $x + 1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 0 & & $x + 1$ & & x & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & x & & $x + 1$ & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x + 1$ & & $x + 1$ & & x & & 1 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

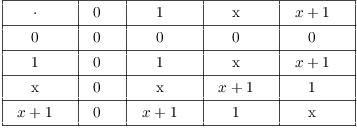
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & x & & $x+1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & x & & $x+1$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & x & & $x+1$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x+1$ & & 0 & & $x+1$ & & 1 & & x & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The addition table is fairly easy to understand: For example, $x + (x + 1) = 1$ , because $2 x = 0 \mod 2$ .

For the multiplication table, take $x \cdot x$ as an example. $x \cdot x = x^2$ ; I apply the Division Algorithm to get

$$x^2 = 1\cdot (x^2 + x + 1) + (x + 1).$$

So $x \cdot x = x + 1 \mod{x^2 + x + 1}$ .

Alternatively, you can use the fact that in the quotient ring $x^2 + x + 1 = 0$ (omitting the coset notation), so $x^2 = x + 1$ (remember that $-1 = 1$ in $\integer_s$ ).

Remark. In the same way, you can construct a field of order $p^n$ for any prime n and any $n \ge 1$ . Just take $\integer_p[x]$ and form the quotient ring $\dfrac{\integer_p[x]}{\langle f(x) \rangle}$ , where $f(x)$ is an irreducible polynomial of degree n.

Example. ( Computations in a quotient ring) (a) Show that $\dfrac{\integer_3[x]}{\langle x^3 + 2 x + 1\rangle}$ is a field.

(b) How many elements are there in $\dfrac{\integer_3[x]}{\langle x^3 + 2 x + 1\rangle}$ ?

(c) Compute

$$\left[(x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle\right] \left[(2 x^2 + 1) + \langle x^3 + 2 x + 1\rangle\right].$$

Express your answer in the form $(ax^2 + bx + c) + \langle x^3 + 2 x + 1\rangle$ , where $a, b, c \in \integer_3$ .

(d) Find $\left[(x^2 + 1) + \langle x^3 + 2 x + 1\rangle\right]^{-1}$ .

(a) $x^3 + 2 x + 1$ has no roots in $\integer_3$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $x^3 + 2 x + 1 \mod{3}$ & & 1 & & 1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Since $x^3 + 2 x + 1$ is a cubic, it follows that it's irreducible. Hence, $\dfrac{\integer_3[x]}{\langle x^3 + 2 x + 1\rangle}$ is a field.

(b) By the Division Algorithm, every element of $\dfrac{\integer_3[x]}{\langle x^3 + 2 x + 1\rangle}$ can be written in the form

$$(a x^2 + b x + c) + \langle x^3 + 2 x + 1\rangle, \quad\hbox{where}\quad a, b, c \in \integer_3.$$

There are 3 choices each for a, b, and c. Therefore, $\dfrac{\integer_3[x]}{\langle x^3 + 2 x + 1\rangle}$ has $3^3 = 27$ elements.

(c)

$$\left[(x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle\right] \left[(2 x^2 + 1) + \langle x^3 + 2 x + 1\rangle\right] = (2 x^4 + 2 x^3 + 2 x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle.$$

By the Division Algorithm,

$$2 x^4 + 2 x^3 + 2 x^2 + x + 2 = (2 x + 2)(x^3 + 2 x + 1) + x^2.$$

Therefore,

$$(2 x^4 + 2 x^3 + 2 x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle = x^2 + \langle x^3 + 2 x + 1\rangle.\quad\halmos$$

(d) Apply the Extended Euclidean algorithm:

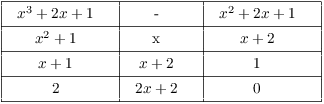
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^3 + 2 x + 1$ & & - & & $x^2 + 2 x + 1$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x^2 + 1$ & & x & & $x + 2$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x + 1$ & & $x + 2$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & $2 x + 2$ & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ (x^2 + 2 x + 1)(x^2 + 1) - (x + 2)(x^3 + 2 x + 1) & = 2 \cr (2 x^2 + x + 2)(x^2 + 1) - (2 x + 1)(x^3 + 2 x + 1) & = 1 \cr}$$

Therefore,

$$\left[(2 x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle\right] \left[(x^2 + 1) + \langle x^3 + 2 x + 1\rangle\right] = 1 + \langle x^3 + 2 x + 1\rangle.$$

Hence,

$$\left[(x^2 + 1) + \langle x^3 + 2 x + 1\rangle\right]^{-1} = (2 x^2 + x + 2) + \langle x^3 + 2 x + 1\rangle.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga