Cardinality

The cardinality of a set is roughly the number of elements in a set. This poses few difficulties with finite sets, but infinite sets require some care.

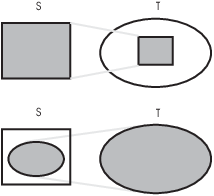
I can tell that two sets have the same number of elements by trying to pair the elements up. Consider the sets

$$\{a, b, c, d\} \quad\hbox{and}\quad \{1, 2, 3, \hbox{Calvin}\}.$$

They have the same number of elements because I can pair the elements of the first set with the elements of the second:

$$\matrix{ a & b & c & d \cr \downarrow & \downarrow & \downarrow & \downarrow \cr 1 & 2 & 3 & \hbox{Calvin} \cr}$$

This kind of pairing is called a bijection or a one-to-one correspondence; it's easy to understand with finite sets, but I need to be more careful if I'm going to use the same idea with infinite sets. I'll begin by reviewing the some definitions and results about functions.

Definition. Let X and Y be sets and let $f: X \to Y$ be a function.

1. f is injective (or one-to-one) if $f(x) = f(y)$ implies $x = y$ .

2. f is surjective (or onto) if for all $y \in Y$ , there is an $x \in X$ such that $f(x) = y$ .

3. f is bijective (or a one-to-one correspondence) if it is injective and surjective.

Definition. Let S and T be sets, and let $f: S \to T$ be a function from S to T. A function $g: T \to S$ is called the inverse of f if

$$g\left(f(s)\right) = s \quad\hbox{for all}\quad s \in S \quad\hbox{and}\quad f\left(g(t)\right) = t \quad\hbox{for all}\quad t \in T.$$

I proved the following result earlier.

Theorem. Let S and T be sets, and let $f: S \to T$ be a function. f is invertible if and only if f is bijective.

Example. Let

$$S = \{a, b, c, d\} \quad\hbox{and}\quad T = \{1, 2, 3, \hbox{Calvin}\}.$$

Define $f: S \to T$ by

$$f(a) = 1, \quad f(b) = 2, \quad f(c) = 3, \quad f(d) = \hbox{Calvin}.$$

Show that f is bijective.

I'll construct an inverse for f. The inverse should "undo" the effect of f:

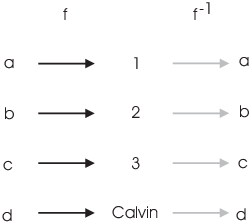
$$\hbox{\epsfysize=2in \epsffile{cardinality-1.eps}}$$

As you can see, I need to define

$$f^{-1}(1) = a, \quad f^{-1}(2) = b, \quad f^{-1}(c) = 3, \quad f^{-1}(\hbox{Calvin}) = d.$$

I've constructed $f^{-1}$ so that $f^{-1}\left(f(s)\right) = s$ for all $s \in S$ . To be complete, I should check that it works the other way, too:

$$f\left(f^{-1}(1)\right) = f(a) = 1, \quad f\left(f^{-1}(2)\right) = f(b) = 2, \quad f\left(f^{-1}(3)\right) = f(c) = 3,$$

$$f\left(f^{-1}(\hbox{Calvin})\right) = f(d) = \hbox{Calvin}.$$

So $f^{-1}$ really is the inverse of f, and f is a bijection. (For that matter, $f^{-1}$ is a bijection as well, because the inverse of $f^{-1}$ is f.)

Notice that this function is also a bijection from S to T:

$$h(a) = 3, \quad h(b) = \hbox{Calvin}, \quad h(c) = 2, \quad h(d) = 1.$$

If there is one bijection from a set to another set, there are many (unless both sets have a single element).

I introduced bijections in order to be able to define what it means for two sets to have the same number of elements. The number of elements in a set is called the cardinality of the set.

Definition. (a) Let S and T be sets. S and T have the same cardinality if there is a bijection f from S to T.

Notation: $|S| = |T|$ means that S and T have the same cardinality.

(b) A set S is finite if it is empty, or if there is a bijection $f: \{1, 2, 3, \ldots, n\} \to S$ for some integer $n \ge 1$ . A set which is not finite is infinite.

(c) If S is a nonempty finite set and there is a bijection $f: \{1, 2, 3, \ldots, n\} \to S$ for some integer $n \ge 1$ , I'll say that S has cardinality n or that S has n elements. In this case, I'll write $|S| = n$ .

At this point, there is an apparently silly issue that needs to be resolved: Could a finite set be bijective with both $\{1, 2, 3\}$ and $\{1, 2, 3, 4\}$ (say)? Of course, everyday experience says that this is impossible. However, mathematicians always take the point of view that if something is really obvious, then it ought to be easy to justify.

Actually, this particular point isn't that simple to justify --- try to prove it yourself! --- but it's true, and I'll omit the proof.

Example. Prove that the set of natural numbers $\natural = \{1, 2, 3, 4, \ldots\}$ has the same cardinality as the set $E = \{2, 4, 6, 8, \ldots\}$ of positive even integers.

Define $f: \natural \to E$ by

$$f(n) = 2n.$$

This function has an inverse $f^{-1}: E \to \natural$ given by

$$f^{-1}(m) = \dfrac{m}{2}.$$

Note that since $m \in E$ , m is even, so m is divisible by 2 and $\dfrac{m}{2}$ is actually a positive integer.

Here's the proof that f and $f^{-1}$ are inverses:

$$f\left(f^{-1}(m)\right) = f\left(\dfrac{m}{2}\right) = 2\cdot \dfrac{m}{2} = m \quad\hbox{for}\quad m \in E,$$

$$f^{-1}\left(f(n)\right) = f^{-1}(2n) = \dfrac{2n}{2} = n \quad\hbox{for}\quad n \in \natural.$$

This situation looks a little strange. E is contained in $\natural$ , but I've just shown that the two sets "have the same number of elements". The only reason this looks funny is that it contradicts your real world experience --- which only deals with finite objects. In fact, it's characteristic of infinite sets that they have the same number of elements as some of their proper subsets.

Informally, a set has the same cardinality as the natural numbers if the elements of an infinite set can be listed:

$$a_1, a_2, a_3, \ldots.$$

In fact, to define listable precisely, you'd end up saying "the set has the same cardinality as the natural numbers". But this is a good picture to keep in mind. I'll show that the real numbers, for instance, can't be arranged in a list in this way.

The next part of this discussion points out that the notion of cardinality behaves the way "the number of things in a set" ought to behave.

Proposition. Let S, T, and U be sets.

(a) The identity function $\id: S \to S$ given by $\id(s) = s$ is a bijection.

(b) The inverse of a bijection is a bijection.

(c) If $f: S \to T$ and $g: T \to U$ are bijections, then the composite $g\cdot f: S \to U$ is a bijection.

Proof. (a) The identity function has an inverse, namely itself. Therefore, the identity function is a bijection.

(b) If $f: S \to T$ is a bijection, then by definition it has an inverse $f^{-1}: T \to S$ . To be inverses means that

$$f^{-1}\left(f(s)\right) = s \quad\hbox{for all}\quad s \in S \quad\hbox{and}\quad f\left(f^{-1}(t)\right) = t \quad\hbox{for all}\quad t \in T.$$

But these equation also say that f is the inverse of $f^{-1}$ , so it follows that $f^{-1}$ is a bijection.

(c) Suppose that $f: S \to T$ and $g: T \to U$ are bijections. Let $f^{-1}: T \to S$ and $g^{-1}:U \to T$ be their respective inverses. I'll prove that $f^{-1} \cdot g^{-1}$ is the inverse of $g \cdot f$ .

$$\matrix{\left[\left(f^{-1} \cdot g^{-1}\right) \cdot \left(g \cdot f\right)\right](s) & = & f^{-1}\left(g^{-1}\left(g\left(f(s)\right)\right)\right) \hfill & \hbox{Definition of composite} \cr & = & f^{-1}\left(f(s)\right) \hfill & g^{-1}\left(g\left(\hbox{junk}\right)\right) = \hbox{junk} \cr & = & s \hfill & f^{-1}\left(f\left(\hbox{junk}\right)\right) = \hbox{junk} \cr}$$

$$\matrix{\left[\left(g \cdot f\right) \cdot\left(f^{-1} \cdot g^{-1}\right)\right](u) & = & g\left(f\left(f^{-1}\left(g^{-1}(u)\right)\right)\right) \hfill & \hbox{Definition of composite} \cr & = & g\left(g^{-1}(u)\right) \hfill & f\left(f^{-1}\left(\hbox{junk}\right)\right) = \hbox{junk} \cr & = & u \hfill & g^{-1}\left(g\left(\hbox{junk}\right)\right) = \hbox{junk} \cr}$$

This proves that $f^{-1} \cdot g^{-1}$ is the inverse of $g\cdot f$ , so $g \cdot f$ is a bijection.

Corollary. Let S, T, and U be sets.

(a) (Reflexivity) $|S| = |S|$ .

(b) (Symmetry) If $|S| = |T|$ , then $|T| = |S|$ .

(c) (Transitivity) If $|S| = |T|$ and $|T| = |U|$ , then $|S| = |U|$ .

In other words, having the same cardinality is an equivalence relation.

Proof. (a) By the lemma, the identity function $\id: S \to S$ is a bijection, so $|S| = |S|$ .

(b) If $|S| = |T|$ , then there is a bijection $f: S \to T$ . By the lemma, $f^{-1}: T \to S$ is a bijection. Therefore, $|T| = |S|$ .

(c) If $|S| = |T|$ and $|T| = |U|$ , then there are bijections $f: S \to T$ and $g: T \to U$ . By the lemma, $g \cdot f: S \to U$ is a bijection, so $|S| = |U|$ .

Example. Prove that the interval $(0, 1)$ has the same cardinality as $\real$ .

First, notice that the open interval $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ has the same cardinality as the real line. To prove this, I have to construct a bijection $f: \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \to \real$ . It's easy: just define

$$f(x) = \tan x.$$

To show that f is bijective, I have to show that it has an inverse; the inverse is $f^{-1}(x) = \arctan x$ .

Now I know that $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ and $\real$ have the same cardinality. Next, I'll show that $(0, 1)$ and $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ have the same cardinality.

The idea is to multiply by $\pi$ to stretch $(0, 1)$ to $(0, \pi)$ . Then I subtract $\dfrac{\pi}{2}$ to shift $(0, \pi)$ to $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ .

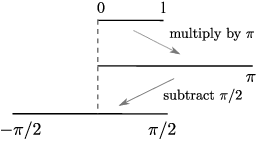
$$\hbox{\epsfysize=1.25in \epsffile{cardinality-2.eps}}$$

All together, I define $g: (0, 1) \to \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ by

$$g(x) = \pi x - \dfrac{\pi}{2}.$$

First, if $0 < x < 1$ , then $0 < \pi x < \pi$ , so $-\dfrac{\pi}{2} < \pi x - \dfrac{\pi}{2} < \dfrac{\pi}{2}$ . This shows that g takes inputs in $(0, 1)$ and produces outputs in $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ .

To show that g is bijective, I have to produce an inverse. The standard "swap the x's and y's" procedure works; you get

$$g^{-1}(x) = \dfrac{x + \dfrac{\pi}{2}}{\pi}.$$

Here's the proof that g and $g^{-1}$ are inverses:

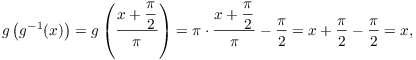
$$g\left(g^{-1}(x)\right) = g\left(\dfrac{x + \dfrac{\pi}{2}}{\pi}\right) = \pi \cdot \dfrac{x + \dfrac{\pi}{2}}{\pi} - \dfrac{\pi}{2} = x + \dfrac{\pi}{2} - \dfrac{\pi}{2} = x,$$

$$g^{-1}\left(g(x)\right) = g^{-1}\left(\pi x - \dfrac{\pi}{2}\right) = \dfrac{\pi x - \dfrac{\pi}{2} + \dfrac{\pi}{2}}{\pi} = \dfrac{\pi x}{\pi} = x.$$

Therefore, g is a bijection, so $(0, 1)$ and $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ have the same cardinality. By transitivity, $(0, 1)$ and $\real$ have the same cardinality.

Example. Prove that $(0, 1)$ has the same cardinality as $\real^+ = (0, \infty)$ .

Define $f: (0, 1) \to (1, \infty)$ by

$$f(x) = \dfrac{1}{x}.$$

Note that if

$$0 < x < 1, \quad\hbox{then}\quad \dfrac{1}{x} > 1.$$

Therefore, f does map $(0, 1)$ to $(1, \infty)$ .

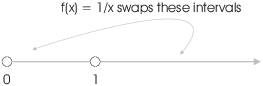
$$\hbox{\epsfysize=0.75in \epsffile{cardinality-3.eps}}$$

I claim that $f^{-1}(x) = \dfrac{1}{x}$ . If $x > 1$ , then $0 < \dfrac{1}{x} < 1$ , so $f^{-1}$ maps $(1, \infty)$ to $(0, 1)$ . Moreover,

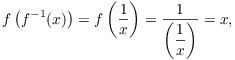
$$f\left(f^{-1}(x)\right) = f\left(\dfrac{1}{x}\right) = \dfrac{1}{\left(\dfrac{1}{x}\right)} = x,$$

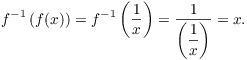
$$f^{-1}\left(f(x)\right) = f^{-1}\left(\dfrac{1}{x}\right) = \dfrac{1}{\left(\dfrac{1}{x}\right)} = x.$$

Thus, f is a bijection.

Define $g: (1, \infty) \to (0, \infty)$ by

$$g(x) = x - 1.$$

If $x > 1$ , then $x - 1 > 0$ . Therefore, g does map $(1, \infty)$ to $(0, \infty)$ .

I claim that $g^{-1}(x) = x + 1$ . If $x > 0$ , then $x + 1 > 1$ , so $g^{-1}$ maps $(0, \infty)$ to $(1, \infty)$ . Moreover,

$$g\left(g^{-1}(x)\right) = g(x + 1) = (x + 1) - 1 = x,$$

$$g^{-1}\left(g(x)\right) = g^{-1}(x - 1) = (x - 1) + 1 = x.$$

Therefore, g is a bijection.

With the bijections f and g, I have $|(0, 1)| = |(1, \infty)| = |(0, \infty)|$ , so $(0, 1)$ and $(0, \infty)$ have the same cardinality.

Example. Prove that the intervals $[0, 4]$ and $[-3, 5]$ have the same cardinality by constructing a bijection from one to the other.

It's important that both of these intervals are closed intervals. If both were open --- say $(-3, 5)$ and $(0, 4)$ --- we can still take the approach we'll take in this example. We would have some difficulty, however, if the intervals were (say) $[-3, 5]$ and $(0, 4)$ . We'll see how to handle that kind of situation later.

The interval $[-3, 5]$ has length 8 and the interval $[0, 4]$ has length 4. Since $2 \cdot 4 = 8$ , I'll define a bijection $f: [0, 4] \to [-3, 5]$ by "scaling up by a factor of 2". So I start this way:

$$f(x) = 2 x \ldots .$$

As it stands, this doesn't work, because $f(0) = 2 \cdot 0 = 0$ , and I'd like 0 to go to -3 in $[-3, 5]$ . I fix this by subtracting 3:

$$f(x) = 2 x - 3.$$

First, I need to show that f actually takes $[0, 4]$ to $[-3, 5]$ . Suppose $x \in [0, 4]$ . Then

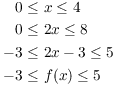
$$\eqalign{ 0 \le\ & x \le 4 \cr 0 \le\ & 2 x \le 8 \cr -3 \le\ & 2 x - 3 \le 5 \cr -3 \le\ & f(x) \le 5 \cr}$$

Hence, $f(x) \in [-3, 5]$ . Therefore, it's valid to write $f: [0, 4] \to [-3, 5]$ .

As usual, I'll show f is bijective by constructing an inverse $g: [-3, 5] \to [0, 4]$ . You can do this by working backward on scratch paper, or by doing a scaling argument like the one I used to construct f. Either way, I get

$$g(x) = \dfrac{1}{2} (x + 3).$$

As I did with f, I need show that g takes its supposed domain $[-3, 5]$ into its supposed codomain $[0, 4]$ . Suppose $x \in [-3, 5]$ . Then

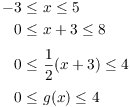
$$\eqalign{ -3 \le\ & x \le 5 \cr 0 \le\ & x + 3 \le 8 \cr \noalign{\vskip2pt} 0 \le\ & \dfrac{1}{2} (x + 3) \le 4 \cr \noalign{\vskip2pt} 0 \le\ & g(x) \le 4 \cr}$$

Thus, $g(x) \in [0, 4]$ . Therefore, it's valid to write $g: [-3, 5] \to [0, 4]$ .

Finally, I need to show f and g are inverses.

$$f(g(x)) = f\left(\dfrac{1}{2} (x + 3)\right) = 2 \cdot \dfrac{1}{2} (x + 3) - 3 = (x + 3) - 3 = x.$$

$$g(f(x)) = g(2 x - 3) = \dfrac{1}{2} [(2 x - 3) + 3] = \dfrac{1}{2} \cdot 2 x = x.$$

Hence, f and g are inverses. Therefore, f and g are bijections. This proves that $[-3, 5]$ and $[0, 4]$ have the same cardinality.

In many situations, it's difficult to show that two sets have the same cardinality by actually constructing a bijection between them. The theorem that follows gives an indirect way to show that two sets have the same cardinality.

Theorem. (Schröder-Bernstein) Let S and T be sets. Suppose there are injective functions $f: S \to T$ and $g: T \to S$ . Then S and T have the same cardinality.

The proof of the Schröder-Bernstein theorem is a little tricky, so I won't do it here.

The Schröder-Bernstein theorem says that if S has the same cardinality as a subset of T, and T has the same cardinality as a subset of S, then S and T must have the same cardinality.

$$\hbox{\epsfysize=1.75in \epsffile{cardinality-4.eps}}$$

It is a powerful tool for showing that sets have the same cardinality. Here are some examples.

Example. Show that the open interval $(0, 1)$ and the closed interval $[0, 1]$ have the same cardinality.

The open interval $0 < x < 1$ is a subset of the closed interval $0 \le x \le 1$ . In this situation, there is an "obvious" injective function $f: (0, 1) \to [0, 1]$ , namely the function $f(x) = x$ for all $x \in (0, 1)$ . (f is called an inclusion map.) If $f(x_1) = f(x_2)$ , then $x_1 = x_2$ , so f is injective.

Next, I'll construct an injective function $g: [0, 1] \to (0, 1)$ . The idea is to find a "copy" of $[0, 1]$ in $(0, 1)$ , then do some scaling and translation to map $[0, 1]$ onto the copy. I'll use the interval $[0.25, 0.75]$ as my target in $(0, 1)$ . The target has length 0.5, so I'll multiply by 0.5 to shrink $[0, 1]$ to $[0,0.5]$ . Next, I'll add 0.25 to shift $[0,0.5]$ to $[0.25, 0.75]$ . All together, I get

$$g(x) = 0.5 x + 0.25 \quad\hbox{for}\quad 0 \le x \le 1.$$

First, if $0 \le x \le 1$ , then $0 \le 0.5 x \le 0.5$ , so $0.25 \le 0.5 x + 0.25 \le 0.75$ . This proves that g is a function from $[0, 1]$ to $[0.25, 0.75]$ .

Next, I need to show that g is injective. Suppose that $g(a) = g(b)$ , I must prove that $a = b$ . Now $g(a) = g(b)$ means that

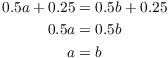
$$\eqalign{ 0.5 a + 0.25 & = 0.5 b + 0.25 \cr 0.5 a & = 0.5 b \cr a & = b \cr}$$

Therefore, g is injective. (In fact, g is bijective, and you could prove injectivity by constructing $g^{-1}$ --- though it would be overdoing it a bit.)

Now I have injective functions $(0, 1) \to [0, 1]$ and $[0, 1] \to (0, 1)$ . By Schröder-Bernstein, $|(0, 1)| = |[0, 1]|$ .

Example. Prove that $[-1, 1]$ has the same cardinality as $(1, 3) \cup (4, 6)$ .

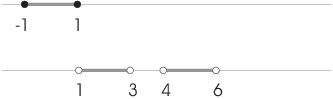
$$\hbox{\epsfxsize=3 in \epsffile{cardinality-5.eps}}$$

The two sets don't "look alike" --- the first set is a single interval which is closed on both ends, while the second set consists of two open intervals. When two sets don't look alike but you think they have the same cardinality, consider using the Schröder-Bernstein theorem. I'll define injective functions going from each set into the other.

I'll describe in words how I'm getting the definitions of the functions. (Note that there are many functions you could use to do this!)

The first set is an interval of length 2, which (because of its endpoints) won't fit in either of the intervals that make up the second set. Since the second set's intervals don't have endpoints, if I just slide $[-1, 1]$ over, its endpoints will stick out of the ends of either $(1, 3)$ or $(4, 6)$ . So the idea is to shrink $[-1, 1]$ first, then slide it inside either $(1, 3)$ or $(4, 6)$ .

If I multiply $[-1, 1]$ by 0.5, I get $[-0.5, 0.5]$ , an interval of length 1. This will surely fit inside $(1, 3)$ (say), and I can slide $[-0.5, 0.5]$ into $(1, 3)$ by adding 2. This takes $[-0.5, 0.5]$ to $[1.5,2.5]$ . I just have to do the two steps one after the other. So define $f: [-1, 1] \to (1, 3) \cup (4, 6)$ by

$$f(x) = 0.5 x + 2.$$

First, I have to show that this makes sense --- that is, that f really takes $[-1, 1]$ into $(1, 3) \cup (4, 6)$ . Suppose $x \in [-1, 1]$ . Then

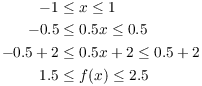
$$\eqalign{ -1 & \le x \le 1 \cr -0.5 & \le 0.5 x \le 0.5 \cr -0.5 + 2 & \le 0.5 x + 2 \le 0.5 + 2 \cr 1.5 & \le f(x) \le 2.5 \cr}$$

Since $1.5 \le f(x) \le 2.5$ , obviously $1 < f(x) < 3$ , so f does map $[-1, 1]$ into $(1, 3) \cup (4, 6)$ .

Next, I have to show that f is injective. Suppose $f(a) = f(b)$ . Then

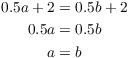
$$\eqalign{ 0.5 a + 2 & = 0.5 b + 2 \cr 0.5 a & = 0.5 b \cr a & = b \cr}$$

Hence, f is injective.

Next, I have to define an injective function $g: (1, 3) \cup (4, 6) \to [-1, 1]$ . Now $(1, 3) \cup (4, 6)$ occupies a total length of $6 - 1 = 5$ , whereas the target interval $[-1, 1]$ has length 2. If I multiply by $\dfrac{1}{5} = 0.2$ , I'll shrink $(1, 3) \cup (4, 6)$ to $(0.2, 0.6) \cup (0.8, 1.2)$ , which has a total length of 1. Next, I can slide $(0.2, 0.6) \cup (0.8, 1.2)$ inside $[-1, 1]$ by subtracting 0.7, which should give $(-0.5, -0.1) \cup (0.1, 0.5)$ .

Thus, define $g: (1, 3) \cup (4, 6) \to [-1, 1]$ by

$$g(x) = 0.2 x - 0.7.$$

I need to check that g maps $(1, 3) \cup (4, 6)$ into $[-1, 1]$ . Let $x \in (1, 3) \cup (4, 6)$ . Then certainly x is between 1 and 6, i.e. $1 < x < 6$ . (Of course, $1 < x < 6$ does not imply that $x \in (1, 3) \cup (4, 6)$ . Do you see why?) So

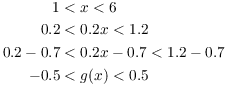
$$\eqalign{ 1 & < x < 6 \cr 0.2 & < 0.2 x < 1.2 \cr 0.2 - 0.7 & < 0.2 x - 0.7 < 1.2 - 0.7 \cr -0.5 & < g(x) < 0.5 \cr}$$

Since $-0.5 < g(x) < 0.5$ , obviously $-1 \le g(x) \le 1$ , so g does map $(1, 3) \cup (4, 6)$ into $[-1, 1]$ .

Next, I have to show that g is injective. Suppose $g(a) = g(b)$ . Then

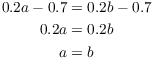
$$\eqalign{ 0.2 a - 0.7 & = 0.2 b - 0.7 \cr 0.2 a & = 0.2 b \cr a & = b \cr}$$

Therefore, g is injective.

Hence, $[-1, 1]$ and $(1, 3) \cup (4, 6)$ have the same cardinality, by the Schröder-Bernstein theorem.

I've already noted that it's easy to find finite sets of different cardinalities: for example, a set with three elements does not have the same cardinality as a set with 42 elements. I've also given examples of infinite sets which have the same cardinality. It's an important fact that not all infinite sets have the same cardinality --- there are different kinds of "infinity"! Here's some terminology which I'll used to describe the situation.

Definition. A set is countably infinite if it has the same cardinality as the natural numbers $\natural = \{1, 2, 3, \ldots\}$ . An infinite set which is not countably infinite is uncountably infinite or uncountable.

A set is countable if it is either finite or countably infinite.

I know that some infinite sets --- the even integers, for instance --- are countably infinite. I know of other infinite sets, such as the real numbers. Is the set of real numbers countably infinite? The answer is no; the proof is due to Georg Cantor (1845--1918), and is called the diagonalization argument.

Theorem. The open interval $(0, 1)$ is uncountably infinite.

Proof. I'm going to be a little informal in this proof so that the main idea isn't lost in a lot of notation.

Suppose on the contrary that $(0, 1)$ is countably infinite. Represent numbers in the interval as decimals $0.a_1 a_2 a_3\ldots$ . (If a number ends in an infinite sequence of 9's, rewrite it as a finite decimal --- so, for instance, $0.134999\ldots$ becomes 0.135.) Since $(0, 1)$ is countably infinite by assumption, I can arrange the numbers in $(0, 1)$ in a list:

$$\hbox{\epsfysize=1.75 in \epsffile{cardinality-6.eps}}$$

I emphasize that, by assumption, this list contains all of the numbers in the interval $(0, 1)$ .

Now go down the diagonal and make a number using the digits. In this case, I get the number $0.30465243\ldots$ .

Take each of the digits in this number and change it to any other digit except 9. For example, you could add 1 to each digit from 0 to 7 and change 8 or 9 to 0. This would produce the number $0.41576354\ldots$ .

(The reason you do not want to change digits to 9 is so that you don't wind up with a number that ends in an infinite sequence of 9's.)

The number $0.41576354\ldots$ differs from each of the numbers in my list. Specifically, the $n^{\rm th}$ digit of $0.41576354\ldots$ is different from the $n^{\rm th}$ digit in the $n^{\rm th}$ number on the list. This means that $0.41576354\ldots$ is not in my list --- which is a contradiction, because I assumed that my list contained all of the numbers in the interval $(0, 1)$ .

Therefore, the interval $(0, 1)$ must be uncountably infinite.

Since the interval $(0, 1)$ has the same cardinality as $\real$ , it follows that $\real$ is uncountably infinite as well. Notice that $\integer$ (which is countably infinite) is a subset of $\real$ . Are there any sets which are "between" $\integer$ and $\real$ in cardinality?

The Continuum Hypothesis states that there are no sets which are "between" $\integer$ and $\real$ in cardinality; it was first stated by Cantor, who was unable to construct a proof. Kurt Gödel [2] proved around 1940 that the Continuum Hypothesis was consistent relative to the standard axioms of set theory. Paul Cohen [1] proved in 1963 that the Continuum Hypothesis is undecidable: It is independent of the standard axioms for set theory.

In other words, the question of the existence of a subset of $\real$ which has cardinality different from either $\integer$ or $\real$ can't be settled without adding assumptions to standard mathematics --- and you can assume either that such a set exists, or that it doesn't, without causing a contradiction.

Definition. Let S be a set. The power set $\powerset(S)$ of S is the set of all subsets of S.

For instance, suppose $S = \{a, b, c\}$ . The power set of S is

$$\powerset(S) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.$$

Notice that the power set includes the empty set and the set S itself.

If you're constructing a subset of a set, there are two alternatives for each element: Either it is in the subset, or it is not. So if the set has n elements, the two alternatives for each element give $2^n$ possibilities in all. Therefore, if S is finite and $|S| = n$ , then $|\powerset(S)| = 2^n$ .

In this example, $|S| = 3$ , and $|\powerset(S)| = 2^3 = 8$ .

Theorem. If S is a set, then S and $\powerset(S)$ do not have the same cardinality.

Proof. Suppose first that $S = \emptyset$ . Now $\emptyset \subset \emptyset$ , so $P(\emptyset) = \{\emptyset\}$ . Hence, $|\emptyset| = 0$ while $|P(\emptyset)| = 1$ , and the result is true in this case.

Now suppose that $S \ne \emptyset$ . I'll prove the result by contradiction. Suppose that $|S| = |\powerset(S)|$ . This means that there is a bijection $f: S \to \powerset(S)$ .

Since f is a bijection, every element of the power set --- that is, every subset of S --- is paired up with an element of S. For example, there must be an element $s \in S$ for which $f(s) = \emptyset$ .

Of course, $s \notin \emptyset$ . So s is an element which is paired up with a subset that doesn't contain it. And in general, f takes an element of S to a subset of S, and that subset either contains the element or it doesn't.

Here's a particular example to help you get your bearings. In the picture below, the set is $S = \{a, b, c, d\}$ and the function f is depicted by the arrows.

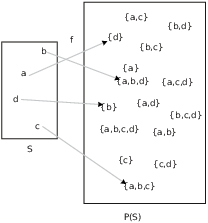
$$\hbox{\epsfysize=2 in \epsffile{cardinality-7.eps}}$$

In this example, f takes b and c to subsets that contain them; f takes a and d to subsets which don't contain them.

Continuing with the proof, let

$$T = \{s \in S \mid s \notin f(s)\}.$$

That is, T is the subset of elements of S which f takes to subsets which don't contain them. I know there is at least one such element, namely the element which f takes to the empty set.

Now f is bijective, and T is a subset of S, so there is an element $s_0 \in S$ such that $f(s_0) = T$ . Question: Is $s_0 \in T$ ?

If $s_0 \in T$ , then by definition of T, $s_0 \notin f(s_0) = T$ . This is a contradiction.

If $s_0 \notin T$ , then $s_0 \notin T = f(s_0)$ , so $s_0$ satisfies the defining condition for T --- which means $s_0 \in T$ . This is a contradiction.

Since $s_0 \in T$ and $s_0 \notin T$ both lead to contradictions, I've actually contradicted my first assumption --- that $|S| = |\powerset(S)|$ . Therefore, $|S| \ne |\powerset(S)|$ , as I wanted to prove.

As an example, the power set of the natural numbers $\natural$ has the same cardinality as $\real$ .

I showed earlier that $\natural$ is countably infinite, whereas $\real$ is uncountably infinite, so this confirms the theorem in this particular case.

Proposition. If X and Y are finite, then $|X \times Y| = |X|\,|Y|$ .

Proof. Here's an informal proof. The elements of $X \times Y$ are ordered pairs $(x, y)$ where $x \in X$ and $y \in Y$ . Since there are $|X|$ choices for x and there are $|Y|$ choices for y, there are $|X|\,|Y|$ such ordered pairs.

More formally, suppose

$$X = \{x_1, x_2, \ldots x_m\} \quad\hbox{and}\quad Y = \{y_1, y_2, \ldots y_n\}.$$

Define a function $f: X \times Y \to \{1, 2, \ldots m n\}$ by

$$f(x_i, y_j) = (i - 1) n + j.$$

I'll let you verifty that it's injective and surjective, and hence, a bijection.

For example, if S has 42 elements and T has 5 elements, then $S \times T$ has $42\cdot 5 = 210$ elements.

Interesting things happen when S and T are infinite. For example, $\natural$ is countably infinite; how big is $\natural \times \natural$ ?

Theorem. $\natural \times \natural$ is countably infinite.

Proof. $\natural \times \natural$ is the set of pairs $(m,n)$ , where m and n are natural numbers:

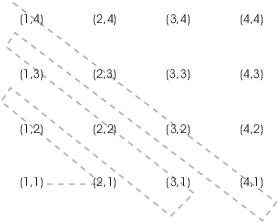
$$\hbox{\epsfysize=2 in \epsffile{cardinality-8.eps}}$$

I'm going to list the pairs starting with $(1,1)$ in the order shown by the grey line. This means I'm constructing a function $f: \natural \times \natural \to \natural$ . Here it is:

$$f(m,n) = \dfrac{(m + n - 2)(m + n - 1)}{2} + m.$$

Here is why this works. $(m,n)$ is the $m^{\rm th}$ element on the diagonal line whose elements add up to $m + n$ . Previous to that, the number of element I've gone through is

$$0 + 1 + 2 + \cdots + (m + n - 2) = \dfrac{(m + n - 2)(m + n - 1)}{2}.$$

That gives $\dfrac{(m + n - 2)(m + n - 1)}{2} + m$ .

It's a little tricky to show f is injective, so I'll omit the proof here. There is an obvious way to make an injective function from $\natural$ to $\natural \times \natural$ :

$$g(n) = (1, n).$$

If $g(n_1) = g(n_2)$ , then $(n_1, 1) = (n_2, 1)$ , so $n_1 = n_2$ , and hence g is injective. By the Schröder-Bernstein theorem, $\natural$ and $\natural \times \natural$ have the same cardinality.

[1] Paul J. Cohen, Set Theory and the Continuum Hypothesis, Reading, Massachusetts: The Benjamin-Cummings Publishing Company, Inc., 1966 [ISBN 0-8053-2327].

[2] Kurt Gödel, Consistency-proof for the generalized continuum hypothesis, Proc. Nat. Acad. Sci. U.S.A., 25(1939), 220-204.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga