Cartesian Products

Definition. Let S and T be sets. The Cartesian product of S and T is the set $S \times T$ consisting of all ordered pairs , where $s \in S$ and $t \in T$ .

Ordered pairs are characterized by the following property: if and only if

$a = c \quad\hbox{and}\quad b = d.$

Remarks. (a) $S \times T$ is not the same as $T \times S$ unless .

(b) You can define an ordered pair using sets. For example, the ordered pair can be defined as the set $\{x, \{x, y\}\}$ .

Example. Let $S = \{a, b, c\}$ and $T = \{1, 2\}$ . List the elements of $S \times T$ and sketch the set.

$S \times T = \{(a, 1), (a, 2), (b,1 ), (b, 2), (c, 1), (c, 2)\}.$

Notice that S and T are not subsets of $S \times T$ . There are subset which "look like" S and T; for example, here's a subset that "looks like" S:

$U = \{(a, 1), (b, 1), (c, 1)\}.$

But this is not S: The elements of S are a, b, and c, whereas the elements of the subset U are pairs.

Here's a picture of $S \times T$ . The elements are points in the grid:

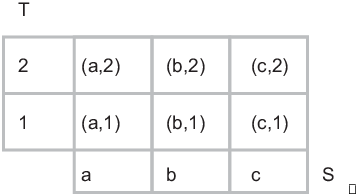
$\hbox{\epsfysize=1.75 in \epsffile{cartesian-products-1.eps}}\quad\halmos$

$\real \times \real$ consists of all pairs , where $x, y \in \real$ . This is the same thing as the the x-y-plane:

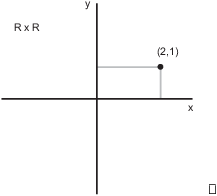
$\hbox{\epsfysize=1.75 in \epsffile{cartesian-products-2.eps}}\quad\halmos$

Example. Consider the following subset of $\real \times \real$ :

$S = \{(2 x, 5 x) \mid x \in \real\}.$

(a) Prove that $(-14, -35) \in S$ .

(b) Prove that $(18, 50) \notin S$ .

(a)

$(-14, -35) = (2 \cdot (-7), 5 \cdot (-7)) \in S.\quad\halmos$

(b) Suppose $(18, 50) \in S$ . Then for some $x \in \real$ , I have

Equating the first components, I get , so . But equating the second components, I get , so . This is a contradiction, so $(18, 50) \notin S$ .

Example. $\integer \times \integer$ is the set of pairs of integers. Consider the following subsets of $\integer \times \integer$ :

$A = \{(3 n + 5, 9 n + 10) \mid n \in \integer\} \quad\hbox{and}\quad B = \{(s, t) \in \integer \times \integer \mid s + t \quad\hbox{is odd}\}.$

Prove that $A \subset B$ .

Let $(3 n + 5, 9 n + 10) \in A$ . B consists of pairs whose components add to an odd number. So I add the components of :

Since is odd, is odd. This proves that $(3 n + 5, 9 n + 10) \in B$ .

You can take the product of more than 2 sets --- even an infinite number of sets, though I won't consider infinite products here.

For example, $\integer \times \integer \times \integer$ consists of ordered triples , where a, b, and c are integers.

Example. Consider the following subset of $\integer \times \integer \times \integer$ :

$W = \{(a, b, a + 2 b) \mid a, b \in \integer\}.$

(a) Show that $(-3, 5, 7) \in W$ .

(b) Show that $(2, -4, 6) \notin W$ .

(a)

$(-3, 5, 7) = (-3, 5, -3 + 2 \cdot 5) \in W.\quad\halmos$

(b) Suppose $(2, -4, 6) \in W$ . Then for some integers a and b, I have

Equating components, I get three equations:

$a = 2, \quad b = -4, \quad a + 2 b = 6.$

But substituting and into gives

$a + 2 b = 2 + 2 \cdot (-4) = -6 \ne 6.$

This contradiction proves that $(2, -4, 6) \notin W$ .

Contact information

Bruce Ikenaga's Home Page