Conditional Proof

A conditional proof is a proof of an "if-then" (conditional) statement.

Since any proof makes some assumptions, you might say that every proof is a conditional proof. But there are different kinds of assumptions you might make. Consider the following conditional statements:

"If $x \in \real$ , then $x^2 + 49 \ge 14 x$ ."

"If $x \in \real$ and $x > 3$ , then $x^2 + 5 x + 2 > 25$ ."

There's an obvious sense in which the "if" part of the second statement has more content that the "if" part of the first statement. In the first statement, the "if" part doesn't give you much to go on. In the second statement, you would suspect that the number 3 is somehow related to the "then" part.

In this section, I'll look at proofs of conditional statements where the "if" part carries that kind of significant information.

Example. Prove that if $x \in \real $ and $x > 3$ , then $x^2 + 5 x + 2 > 25$ .

To prove the statement, you assume that $x > 3$ . Now

$$x > 3, \quad\hbox{so}\quad x^2 > 9.$$

Likewise,

$$x > 3, \quad\hbox{so}\quad 5 x > 15.$$

If I add $x^2 > 9$ and $5 x > 15$ , I get $x^2 + 5 x > 24$ . I compare this inequality to the target inequality, and I see that I'm missing a "2" on the left and a "1" on the right. Well, $2 > 1$ , so adding this inequality to $x^2 + 5 x > 24$ , I obtain

$$x^2 + 5 x + 2 > 25.$$

Notice the conditional nature of the conclusion. It's certainly not true that $x^2 + 5 x + 2 > 25$ for any real number x. (For example, it's false if $x = 0$ .) The conclusion is true if the assumption $x > 3$ is true.

The last example shows how you write a conditional proof. In this situation, you're trying to prove a statement of the form $P \ifthen Q$ , where P is the set of assumptions --- it may be one statement, or several statements --- and Q is the conclusion. You assume P and try to derive Q. If you succeed, then $P \ifthen Q$ is true.

Example. (a) Prove that if x is a real number and $x > 2$ , then $x^3 - 3 x^2 + 2 x > 0$ .

(b) Give a specific example to show that the converse is false.

(a) Suppose $x > 2$ . Then

$$x - 2 > 0, \quad x - 1 > 2 - 1 = 1 > 0, \quad x > 2 > 0.$$

Thus, $x - 2$ , $x - 1$ , and x are all positive. The product of positive numbers is positive, so

$$x^3 - 3 x ^2 - 2 x = x(x - 1)(x - 2) > 0.\quad\halmos$$

(b) Take $x = 0.5$ . Then

$$(0.5)^3 - 3 (0.5)^2 + 2 (0.5) = 0.375 > 0.$$

However, $0.5 \not> 2$ .

For the next few examples, recall that an integer n is even if it can be written as $n = 2 m$ for some integer m.

An integer n is odd if it can be written as $n = 2 m + 1$ for some integer m.

Example. ( Proving the contrapositive) Let n be an integer. Prove that if $3 n^2 + 5 n + 18$ is not even, then n is not even.

Recall that the conditional $P \ifthen Q$ is logically equivalent to its contrapositive $\lnot Q \ifthen \lnot P$ . In some cases, you use this to prove a conditional statement by replacing it with its contrapositive.

In this example, the given conditional statement is kind of awkward: Both the "if" and "then" parts are negative statements. And if I try to prove this conditional statement by assuming the "if" part --- that is, assuming that $3 n^2 + 5 n + 18$ is not even --- it isn't obvious how to proceed.

Instead, I replace the statement with its contrapositive: "If n is even, then $3 n^2 + 5 n + 18$ is even."

Begin by assuming the "if" part: Suppose n is even. By definition, this means that $n = 2 m$ , where m is an integer. Then

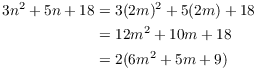
$$\eqalign{ 3 n^2 + 5 n + 18 & = 3 (2 m)^2 + 5 (2 m) + 18 \cr & = 12 m^2 + 10 m + 18 \cr & = 2(6 m^2 + 5 m + 9) \cr}$$

Now $6 m^2 + 5 m + 9$ is an integer, so $2(6 m^2 + 5 m + 9)$ is even (by definition of "even"). Hence, $3 n^2 + 5 n + 18$ is even.

Since I've proved the contrapositive, this proves the original statement.

If a and b are integers, a divides b means that there is an integer c such that $a c = b$ . a divides b is written $a \mid b$ for short.

For example, $6 \mid 18$ because $6 \cdot 3 = 18$ , $10 \mid 0$ because $10 \cdot 0 = 0$ , and $-6 \mid 6$ since $(-6) \cdot (-1) = 6$ .

On the other hand, 3 does not divide 5, since there is no integer c such that $3 \cdot c = 5$ . "3 does not divide 5" is written $3 \notdiv 5$ .

Note that an integer n is even if and only if $2 \mid n$ .

Example. Prove that if n is an integer and n is divisible by 3, then $2 n^2 + 5 n + 12$ is divisible by 3.

Note that you have to prove this directly from the definition and rules of algebra; you can't assume "obvious" things like "the sum of numbers divisible by 3 is divisible by 3" (unless you prove these "obvious" things first!).

Suppose n is divisible by 3. Then $n = 3 m$ for some integer m. So

$$2 n^2 + 5 n + 12 = 2 (3 m)^2 + 5 (3 m) + 12 = 18 m^2 + 15 m + 12 = 3 (6 m^2 + 5 m + 12).$$

The last expression is 3 times an integer. Hence, $2 n^2 + 5 n + 12$ is divisible by 3.

Note that I didn't stop with "$18 m^2 + 15 m + 12$ " and say "the sum of integers divisible by 3 must be divisible by 3". That's true, but I haven't proved it. Can you do it?

Example. Prove that if n is odd, then $n^2$ leaves a remainder of 1 when it is divided by 4.

I assume that n is an odd number. I want to prove that $n^2$ leaves a remainder of 1 when it is divided by 4.

An odd number is an integer which can be written in the form $2 m + 1$ for some integer m. Since n is odd, $n = 2 m + 1$ for some m.

Squaring n, I get

$$n^2 = (2 m + 1)^2 = 4 m^2 + 4 m + 1 = 4(m^2 + m) + 1.$$

Since $4(m^2 + m)$ is divisible by 4, $n^2$ leaves a remainder of 1 when it is divided by 4.

This proves the conditional statement that if n is odd, then $n^2$ leaves a remainder of 1 when it is divided by 4.

A conditional proof in logic will be a proof of a statement of the form "$P \ifthen Q$ ". To do this:

(a) State the premises.

(b) Introduce P as a new premise. Label it "Premise for conditional proof".

(c) Prove Q from P and the given premises using rules of inference as usual.

(d) Conclude "$P \ifthen Q$ ". Label it "Conditional proof", and include the numbers of the statements for P and for Q.

Example. Premises: $\left\{\matrix{(A \lor \lnot C) \ifthen B \cr \lnot D \ifthen \lnot B \cr}\right.$

Prove: $A \ifthen D$ .

To prove the conditional statement $A \ifthen D$ , I assume the "if" part A and try to prove the "then" part D.

$$\matrix{ 1. \hfill & (A \lor \lnot C) \ifthen B \hfill & \hbox{Premise} \hfill \cr 2. \hfill & \lnot D \ifthen \lnot B \hfill & \hbox{Premise} \hfill \cr 3. \hfill & A \hfill & \hbox{Premise for conditional proof} \hfill \cr 4. \hfill & A \lor \lnot C \hfill & \hbox{Constructing a disjunction} \hfill \cr 5. \hfill & B \hfill & \hbox{Modus ponens (1, 4)} \hfill \cr 6. \hfill & D \hfill & \hbox{Modus tollens (2, 5)} \hfill \cr 7. \hfill & A \ifthen D \hfill & \hbox{Conditional proof (3, 6)} \hfill \cr}$$

The then-part D was proved in line 6. Together with the if-part A in line 3, this proves the conditional $A \ifthen D$ .

Example. Premises: $\left\{\matrix{A \land \lnot D \cr B \ifthen (C \ifthen D) \cr}\right.$

Prove: $(A \ifthen B) \ifthen\, \lnot C$ .

To prove the conditional statement $(A \ifthen B) \ifthen\,\lnot C$ , I assume the "if" part $A \ifthen B$ and try to prove the "then" part $\lnot C$ .

$$\matrix{ \hfill 1. & A \land \lnot D \hfill & \hbox{Premise} \hfill \cr \hfill 2. & B \ifthen (C \ifthen D) \hfill & \hbox{Premise} \hfill \cr \hfill 3. & A \ifthen B \hfill & \hbox{Premise for conditional proof} \hfill \cr \hfill 4. & A \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr \hfill 5. & B \hfill & \hbox{Modus ponens (1,3)} \hfill \cr \hfill 6. & C \ifthen D \hfill & \hbox{Modus ponens (2,5)} \hfill \cr \hfill 7. & \lnot D \hfill & \hbox{Decomposing a conjunction (1)} \hfill \cr \hfill 8. & \lnot C \hfill & \hbox{Modus tollens (6,7)} \hfill \cr \hfill 9. & (A \ifthen B)\ifthen\, \lnot C \hfill & \hbox{Conditional proof (3,8)} \hfill \cr}$$

The then-part $\lnot C$ was deduced on line 8. Together with the if-part $A \ifthen B$ in line 3, this proves the conditional $(A \ifthen B) \ifthen\,\lnot C$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga