Functions

Definition. A function f from a set X to a set Y is a subset f of the product $X \times Y$ such that if $(x, y_1), (x, y_2) \in f$ , then $y_1 = y_2$ .

Instead of writing $(x, y) \in f$ , you usually write $f(x) = y$ . In ordinary terms, to say that an ordered pair $(x, y)$ is in f means that x is the "input" to f and y is the corresponding "output".

The requirement that $(x, y_1), (x, y_2) \in f$ implies $y_1 = y_2$ means that there is a unique output for each input. (It's what is referred to as the "vertical line test" for a graph to be a function graph.)

(Why not say, as in precalculus or calculus classes, that a function is a rule that assigns a unique element of Y to each element of X? The problem is that the word "rule" is ambiguous. The definition above avoids this by identifying a function with its graph.)

The notation $f: X \to Y$ means that f is a function from X to Y.

X is called the domain, and Y is called the codomain. The image (or range) of f is the set of all outputs of the function:

$$\im f = \{y \in Y \mid y = f(x) \hbox{ for some } x \in X\}.$$

Note that the domain and codomain are part of the definition of a function. For example, consider the following functions:

$$f: \real \to \real \quad\hbox{given by}\quad f(x) = x^2.$$

$$g: \real \to \real^{\ge 0} \quad\hbox{given by}\quad g(x) = x^2.$$

$$h: \real^{\ge 0} \to \real \quad\hbox{given by}\quad h(x) = x^2.$$

These are different functions; they're defined by the same rule, but they have different domains or codomains.

Example. Suppose $f: \real \to \real$ is given by

$$f(x) = (\hbox{an integer bigger than x}).$$

Is this a function?

This does not define a function. For example, $f(2.6)$ could be 3, since 3 is an integer bigger than 2.6. But it could also be 4, or 67, or 101, or .... This "rule" does not produce a unique output for each input.

Mathematicians say that such a function --- or such an attempted function --- is not well-defined.

In basic algebra and calculus, functions $\real \to \real$ are often given by rules, without mention of a domain and codomain. In this case, the natural domain ("domain" for short) is the largest subset of $\real$ consisting of numbers which can be "legally" plugged into the function.

Example. Find the natural domain of

$$f(x) = \dfrac{\sqrt{x}}{x - 2}.$$

(i) I must have $x \ge 0$ in order for $\sqrt{x}$ to be defined.

(ii) I must have $x \ne 2$ in order to avoid division by zero.

Hence, the domain of f is $[0, 2) = (2,+\infty)$ .

Example. Define $f: \real - \{2\} \to \real$ by

$$f(x) = \dfrac{3 x}{x - 2}.$$

Prove that $\im f = \{y \mid y \ne 3\}$ .

In words, the claim is that the outputs of y consist of all numbers other than 3. To see why 3 might be omitted, note that

$$\lim_{x \to \infty} \dfrac{3 x}{x - 2} = 3.$$

That is, $y = 3$ is a horizontal asymptote for the graph. Now this isn't a proof, because a graph can cross a horizontal asymptote; it just provides us with a "guess".

To prove $\im f = \{y \mid y \ne 3\}$ , I'll show each set is contained in the other.

Suppose $y \ne 3$ . On scratch paper, I solve $y = \dfrac{3 x}{x - 2}$ for x in terms of y and get $x = \dfrac{2 y}{3 - y}$ . (This is defined, since $y \ne 3$ .) Now I prove that this input produces y as an output:

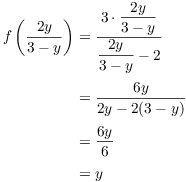
$$\eqalign{ f\left(\dfrac{2 y}{3 - y}\right) & = \dfrac{3 \cdot \dfrac{2 y}{3 - y}}{\dfrac{2 y}{3 - y} - 2} \cr \noalign{\vskip2pt} & = \dfrac{6 y}{2 y - 2(3 - y)} \cr \noalign{\vskip2pt} & = \dfrac{6 y}{6} \cr \noalign{\vskip2pt} & = y \cr}$$

This proves that $y \in \im f$ , so $\{y \mid y \ne 3\} \subset \im f$ .

Conversely, suppose $y \in im f$ , so $y = f(x)$ for some x. I must show that $y \ne 3$ . I'll use proof by contradiction: Suppose $y = 3$ . Then

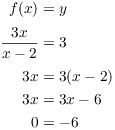
$$\eqalign{ f(x) & = y \cr \noalign{\vskip2pt} \dfrac{3 x}{x - 2} & = 3 \cr \noalign{\vskip2pt} 3 x & = 3(x - 2) \cr 3 x & = 3 x - 6 \cr 0 & = -6 \cr}$$

This contradiction proves $y \ne 3$ . Thus, $\im f \subset \{y \mid y \ne 3\}$ .

Therefore, $\im f = \{y \mid y \ne 3\}$ .

Definition. Let A, B, and C be sets, and let $f: A \to B$ and $g: B \to C$ be functions. The composite of f and g is the function $g\circ f: A \to C$ defined by

$$(g\circ f)(a) = g(f(a)).$$

In my opinion, the notation "$g \circ f$ " looks a lot like multiplication, so (at least when elements are involved) I prefer to write "$g(f(x))$ " instead. However, the composite notation is used often enough that you should be familiar with it.

Example. Define $f: \real \to \real$ by $f(x) = x^3$ and $g: \real \to \real$ by $g(x) = x + 1$ . Find $(g \circ f)(x)$ and $(f \circ g)(x)$ .

$$(g \circ f)(x) = g(f(x)) = g(x^3) = x^3 + 1,$$

$$(f \circ g)(x) = f(g(x)) = f(x + 1) = (x + 1)^3.\quad\halmos$$

Example. Define $f: \real^2 \to \real^2$ and $g: \real^2 \to \real^2$ by

$$f(x, y) = (x + y, x^2 + y) \quad\hbox{and}\quad g(x, y) = (y^3, x + y).$$

Find:

(a) $f(g(x, y))$ .

(b) $f(f(x, y))$ .

(a)

$$f(g(x, y)) = f(y^3, x + y) = (y^3 + (x + y), (y^3)^2 + (x + y)) = (x + y + y^3, x + y + y^6).$$

(b)

$$f(f(x, y)) = f(x + y, x^2 + y) = ((x + y) + (x^2 + y), (x + y)^2 + (x^2 + y)) = (x^2 + 2 x + y, 2 x^2 + 2 x y + y^2 + y).\quad\halmos$$

If you get confused doing this, keep in mind two things:

(i) The variables used in defining a function are "dummy variables" --- just placeholders. For example, $f(a, b) = (a + b, a^2 + b)$ defines the same function f as above.

(ii) The variables are "positional", so in "$f(x, y)$ " the "x" stands for "the first input to f" and the "y" stands for "the second input to f". In fact, you might find it helpful to rewrite the definition of f this way:

$$f((\hbox{first}), (\hbox{second})) = ((\hbox{first}) + (\hbox{second}), (\hbox{first})^2 + (\hbox{second})).$$

Definition. Let X and Y be sets. A function $f: X \to Y$ is:

(a) Injective if for all $x_1, x_2 \in X$ , $f(x_1) = f(x_2)$ implies $x_1 = x_2$ .

(b) Surjective if for all $y \in Y$ , there is an $x \in X$ such that $f(x) = y$ .

(c) Bijective if it is injective and surjective.

Intuitively, a function is injective if different inputs give different outputs. The older terminology for "injective" was "one-to-one".

For functions $\real \to \real$ , "injective" means every horizontal line hits the graph at most once.

A function is surjective if every element of the codomain (the "target set") is an output of the function. The older terminology for "surjective" was "onto".

For functions $\real \to \real$ , "injective" means every horizontal line hits the graph at least once.

A function is bijective if the elements of the domain and the elements of the codomain are "paired up". The older terminology for "bijective" was "one-to-one correspondence".

For functions $\real \to \real$ , "bijective" means every horizontal line hits the graph exactly once.

Note: These are useful pictures to keep in mind, but don't confuse them with the definitions!

Example. (a) Prove that $f: \real \to \real$ given by $f(x) = x^2$ is neither injective nor surjective.

(b) Prove that $f: \real \to \real^{\ge 0}$ given by $f(x) = x^2$ is not injective, but it is surjective.

(c) Prove that $f: \real^{\ge 0} \to \real^{\ge 0}$ given by $f(x) = x^2$ is injective and surjective.

(a) It is not injective, since $f(-3) = 9$ and $f(3) = 9$ : Different inputs may give the same output.

It is not surjective, since there is no $x \in \real$ such that $f(x) = -1$ .

(b) It is not injective, since $f(-3) = 9$ and $f(3) = 9$ : Different inputs may give the same output.

It is surjective, since if $y \ge 0$ , $\sqrt{y}$ is defined, and

$$f(\sqrt{y}) = (\sqrt{y})^2 = y.\quad\halmos$$

(c) It is injective, since if $f(a) = f(b)$ , then $a^2 = b^2$ . But in this case, $a, b \ge 0$ , so $a = b$ by taking square roots.

It is surjective, since if $y \ge 0$ , then $\sqrt{y}$ is defined, and

$$f(\sqrt{y}) = (\sqrt{y})^2 = y.\quad\halmos$$

Notice that in this example, the same "rule" --- $f(x) = x^2$ --- was used, but whether the function was injective or surjective changed. The domain and codomain are part of the definition of a function.

Example. Let $f: \real - \{0\} \to \real$ be given by

$$f(x) = \dfrac{x + 1}{x}.$$

Prove that f is injective.

Suppose $a, b \in \real - \{0\}$ and $f(a) = f(b)$ . I must prove that $a = b$ .

$f(a) = f(b)$ means that $\dfrac{a + 1}{a} = \dfrac{b + 1}{b}$ . Clearing denominators and doing some algebra, I get

$$b(a + 1) = a(b + 1), \quad b a + b = a b + a, \quad a = b.$$

Therefore, f is injective.

Example. Let $f: \real \to \real$ be given by

$$f(x) = 3 x^7 + 5 x^3 + 13 x + 8.$$

Prove that f is injective.

It would probably be difficult to prove this directly. Instead, I'll use the following fact:

Suppose $f: \real \to \real$ is differentiable, and that $f'(x) > 0$ for all x or $f'(x) < 0$ for all x. Then f is injective.

In this case, note that, since even powers are nonnegative,

$$f'(x) = 21 x^6 + 15 x^2 + 13 > 0.$$

Since the derivative is always positive, f is always increasing, and hence f is injective.

Here's a proof of the result I used in the last example.

Proposition. Suppose $f: \real \to \real$ is differentiable, and that $f'(x) > 0$ for all x or $f'(x) < 0$ for all x. Then f is injective.

Proof. Suppose that f is differentiable and always increasing. Suppose that $f(a) = f(b)$ . I want to prove that $a = b$ .

Suppose on the contrary that $a \ne b$ . There's no harm in assuming $a < b$ (otherwise, switch them). By the Mean Value Theorem, there is a number c such that $a < c < b$ and

$$\dfrac{f(b) - f(a)}{b - a} = f'(c).$$

Since $f(a) = f(b)$ and $f'(x) > 0$ for all x,

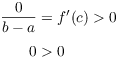
$$\eqalign{ \dfrac{0}{b - a} & = f'(c) > 0 \cr \noalign{\vskip2pt} 0 & > 0 \cr}$$

This contradiction proves that $a = b$ . Therefore, f is injective.

The same proof works with minor changes if $f'(x) < 0$ for all x.

Example. Define $f: \real - \{0\} \to \real - \{1\}$ by

$$f(x) = \dfrac{x + 1}{x}.$$

Prove that f is surjective.

Note that $\real - \{1\}$ is the real numbers other than 1.

Let $y \in \real - \{1\}$ . I have to show that there is an x such that $f(x) = y$ .

I work backwards on scratch paper:

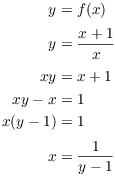
$$\eqalign{ y & = f(x) \cr \noalign{\vskip2pt} y & = \dfrac{x + 1}{x} \cr \noalign{\vskip2pt} x y & = x + 1 \cr x y - x & = 1 \cr x (y - 1) & = 1 \cr \noalign{\vskip2pt} x & = \dfrac{1}{y - 1} \cr}$$

Note that this is not a proof --- I started with $y = f(x)$ , which is what I want to show.

The last line tells me what I need to use for "x". To prove surjectivity, I plug it in and verify that it works. Remember that at this point, I've been given y. So

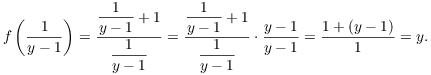
$$f\left(\dfrac{1}{y - 1}\right) = \dfrac{\dfrac{1}{y - 1} + 1}{\dfrac{1}{y - 1}} = \dfrac{\dfrac{1}{y - 1} + 1}{\dfrac{1}{y - 1}} \cdot \dfrac{y - 1}{y - 1} = \dfrac{1 + (y - 1)}{1} = y.$$

Thus, given $y \in \real -\{1\}$ , I have found an input to f which produces y as an output. Therefore, f is surjective.

The preceding example relied on being able to solve for x in terms of y. In general, you can't expect to solve an arbitrary equation for one variable in terms of another. In some cases, it's possible to prove surjectivity indirectly.

Example. Define $f: \real \to \real$ by $f(x) = x^2(x - 1)$ . Show that f is not injective, but that f is surjective. f is not injective, since $f(0) = 0$ and $f(1) = 0$ .

The graph suggests that f is surjective. To say that every $y \in \real$ is an output of f means graphically that every horizontal line crosses the graph at least once (whereas injectivity means that every horizontal line crosses that graph at most once).

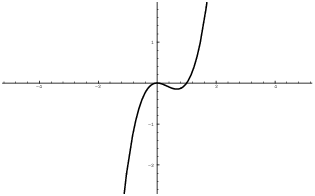
$$\hbox{\epsfysize=1.75in \epsffile{functions-2.eps}}$$

To prove that f is surjective, take $y \in \real$ . I must find $x \in \real$ such that $f(x) = y$ , i.e. such that $x^2(x - 1) = y$ .

The problem is that finding x in terms of y involves solving a cubic equation. This is possible, but it's easy to change the example to produce a function where solving algebraically is impossible in principle.

Instead, I'll proceed indirectly.

$$\lim_{x \to +\infty} x^2(x - 1) = +\infty \quad\hbox{and}\quad \lim_{x \to -\infty} x^2(x - 1) = -\infty.$$

It follows from the definition of these infinite limits that there are numbers a and b such that

$$f(a) < y \quad\hbox{and}\quad f(b) > y.$$

The existence of a comes from $\displaystyle \lim_{x \to -\infty} x^2(x - 1) = -\infty$ , which means that $f(x)$ must eventually become smaller than any number y as $x \to -\infty$ . Likewise, the existence of b comes from $\displaystyle \lim_{x \to +\infty} x^2(x - 1) = +\infty$ , which means that $f(x)$ must eventually become larger than any number y as $x \to \infty$ .

But f is continuous --- it's a polynomial --- so by the Intermediate Value Theorem, there is a point c such that $a < c < b$ and $f(c) = y$ . This proves that f is surjective.

Note, however, that I haven't found c; I've merely shown that such a value c must exist.

Example. Define

$$f(x) = \cases{x + 1 & if $x < 0$ \cr x^2 & if $x \ge 0$ \cr}.$$

Prove that f is surjective, but not injective.

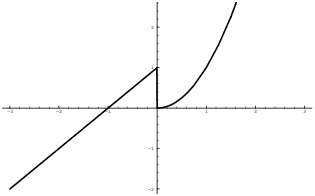
$$\hbox{\epsfysize=1.75in \epsffile{functions-3.eps}}$$

Let $y \in \real$ . If $y < 0$ , then $y - 1 < -1 < 0$ , so

$$f(y - 1) = (y - 1) + 1 = y.$$

If $y \ge 0$ , then $\sqrt{y}$ is defined and $\sqrt{y} \ge 0$ , so

$$f(\sqrt{y}) = (\sqrt{y})^2 = y.$$

This proves that f is surjective.

However,

$$f\left(-\dfrac{3}{4}\right) = -\dfrac{3}{4} + 1 = \dfrac{1}{4} \quad\hbox{and}\quad f\left(\dfrac{1}{2}\right) = \left(\dfrac{1}{2}\right)^2 = \dfrac{1}{4}.$$

Hence, f is not injective.

Example. Consider the function $f: \real^2 \to \real^2$ defined by

$$f(x, y) = (2 x + 4 y, -x - 2 y).$$

Prove that f is neither injective nor surjective.

$$f(0, 0) = (0, 0) \quad\hbox{and}\quad f(2,-1) = (0, 0).$$

Therefore, f is not injective.

To prove f is not surjective, I must find a point $(a, b) \in \real^2$ which is not an output of f. I'll show that $(1, 1)$ is not an output of f. Suppose on the contrary that $f(x, y) = (1, 1)$ . Then

$$(2 x + 4 y, -x - 2 y) = (1, 1).$$

This gives two equations:

$$2 x + 4 y = 1, \quad -x - 2 y = 1.$$

Multiply the second equation by -2 to obtain $2 x + 4 y = -2$ . Now I have $2 x + 4 y = 1$ and $2 x + 4 y = -2$ , so $1 = -2$ , a contradiction.

Therefore, there is no such $(x, y)$ , and f is not surjective.

Example. Let $f: \real^2 \to \real^2$ be defined by

$$f(x, y) = (e^x + y, y^3).$$

Is f injective? Is f surjective?

First, I'll show that f is injective. Suppose $f(a, b) = f(c, d)$ . I have to show that $(a, b) = (c, d)$ .

$$\eqalign{f(a, b) &= f(c, d) \cr (e^a + b, b^3) &= (e^c + d, d^3) \cr}$$

Equating the second components, I get $b^3 = d^3$ . By taking cube roots, I get $b = d$ . Equating the first components, I get $e^a + b = e^c + d$ . But $b = d$ , so subtracting $b = d$ I get $e^a = e^c$ . Now taking the log of both sides gives $a = c$ . Thus, $(a, b) = (c, d)$ , and f is injective.

I'll show that f is not surjective by showing that there is no input $(x, y)$ which gives $(-1, 0)$ as an output. Suppose on the contrary that $f(x, y) = (-1, 0)$ . Then

$$\eqalign{f(x, y) &= (-1, 0) \cr (e^x + y, y^3) &= (-1, 0) \cr}$$

Equating the second components gives $y^3 = 0$ , so $y = 0$ . Equating the first components gives $e^x + y = -1$ . But $y = 0$ , so I get $e^x = -1$ . This is impossible, since $e^x$ is always positive. Therefore, f is not surjective.

Definition. Let S and T be sets, and let $f: S \to T$ be a function from S to T. A function $g: T \to S$ is called the inverse of f if

$$g\left(f(s)\right) = s \quad\hbox{for all}\quad s \in S \quad\hbox{and}\quad f\left(g(t)\right) = t \quad\hbox{for all}\quad t \in T.$$

Not all functions have inverses; if the inverse of f exists, it's denoted $f^{-1}$ . (Despite the crummy notation, "$f^{-1}$ " does not mean "$\dfrac{1}{f}$ ".)

You've undoubtedly seen inverses of functions in other courses; for example, the inverse of $f(x) = x^3$ is $f^{-1}(x) = x^{1/3}$ . However, the functions I'm discussing may not have anything to do with numbers, and may not be defined using formulas.

Example. Define $f: \real - \{-1\} \to \real - \{1\}$ by $f(x) = \dfrac{x}{x + 1}$ . Find the inverse of f.

To find the inverse of f (if there is one), set $y = \dfrac{x}{x + 1}$ . Swap the x's and y's, then solve for y in terms of x:

$$x = \dfrac{y}{y + 1}, \quad x(y + 1) = y, \quad x y + x = y, \quad x = y - x y, \quad x = y(1 - x), \quad y = \dfrac{x}{1 - x}.$$

Thus, $f^{-1}(x) = \dfrac{x}{1 - x}$ . To prove that this works using the definition of an inverse function, do this:

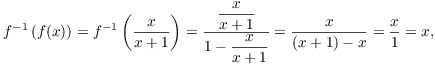
$$f^{-1}\left(f(x)\right) = f^{-1}\left(\dfrac{x}{x + 1}\right) = \dfrac{\dfrac{x}{x + 1}}{1 - \dfrac{x}{x + 1}} = \dfrac{x}{(x + 1) - x} = \dfrac{x}{1} = x,$$

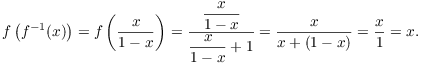
$$f\left(f^{-1}(x)\right) = f\left(\dfrac{x}{1 - x}\right) = \dfrac{\dfrac{x}{1 - x}}{\dfrac{x}{1 - x} + 1} = \dfrac{x}{x + (1 - x)} = \dfrac{x}{1} = x.$$

Recall that the graphs of f and $f^{-1}$ are mirror images across the line $y = x$ :

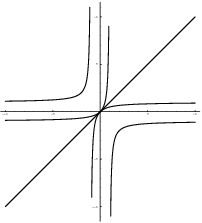
$$\hbox{\epsfysize=2in \epsffile{functions-1.eps}}$$

I'm mentioning this to connect this discussion to things you've already learned. However, you should not make the mistake of equating this special case with the definition. The inverse of a function is not defined by "swapping x's and y's and solving" or "reflecting the graph about $y = x$ ". A function might not involve numbers or formulas, and a function might not have a graph. The inverse of a function is what the definition says it is --- nothing more or less.

Lemma. Let $f: X \to Y$ and $g: Y \to Z$ be invertible functions. Then $g \circ f$ is invertible, and its inverse is

$$(g \circ f)^{-1} = f^{-1} \circ g^{-1}.$$

Proof. Let $x \in X$ and let $z \in Z$ . Then

$$(f^{-1} \circ g^{-1})\circ(g \circ f)(x) = f^{-1}\left(g^{-1}\left(g\left(f(x)\right)\right)\right) = f^{-1}\left(f(x)\right) = x,$$

$$(g \circ f) \circ (f^{-1} \circ g^{-1})(z) = g\left(f\left(f^{-1}\left(g(z)\right)\right)\right) = g\left(g(z)\right) = z.$$

This proves that $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$ .

The next result relates bijectivity and inverses. I'll often use it in showing that a given function is bijective.

Theorem. Let S and T be sets, and let $f: S \to T$ be a function. f is invertible if and only if f is bijective.

Proof. ($\rightarrow$ ) Suppose that f is bijective. I'll construct the inverse function $f^{-1}: T \to S$ .

Take $t \in T$ . Since f is surjective, there is an element $s \in S$ such that $f(s) = t$ . Moreover, s is unique: If $f(s) = t$ and $f(s') = t$ , then $f(s) = f(s')$ . But f is injective, so $s = s'$ .

Define

$$f^{-1}(t) = s.$$

I have defined a function $f^{-1}: T \to S$ . I must show that it is the inverse of f.

Let $s \in S$ . By definition of $f^{-1}$ , to compute $f^{-1}\left(f(s)\right)$ I must find an element $\hbox{FOO} \in S$ such that $f(\hbox{FOO}) = f(s)$ . But this is easy --- just take $\hbox{FOO} = s$ . Thus, $f^{-1}\left(f(s)\right) = s$ .

Going the other way, let $t \in T$ . By definition of $f^{-1}$ , to compute $f\left(f^{-1}(t)\right)$ I find an element $s \in S$ such that $f(s) = t$ . Then $f^{-1}(t) = s$ , so

$$f\left(f^{-1}(t)\right) = f(s) = t.$$

Therefore, $f^{-1}$ really is the inverse of f.

($\leftarrow$ ) Suppose f has an inverse $f^{-1}: T \to S$ . I must show f is injective and surjective.

To show that f is surjective, take $t \in T$ . Then $f\left(f^{-1}(t)\right) = t$ , so I've found an element of S --- namely $f^{-1}(t)$ --- which f maps to t. Therefore, f is surjective.

To show that f is injective, suppose $s_1, s_2 \in S$ and $f(s_1) = f(s_2)$ . Then

$$f^{-1}\left(f(s_1)\right) = f^{-1}\left(f(s_2)\right), \quad\hbox{so}\quad s_1 = s_2.$$

Therefore, f is injective.

Corollary. The composite of bijective functions is bijective.

Proof. Since a function is bijective if and only if it has an inverse, the corollary follows from the fact that the composite of invertible functions is invertible.

Example. Consider the function $f: \real^2 \to \real^2$ defined by

$$f(x, y) = (2 x + y^3, x + 1).$$

Show that f is injective and surjective by constructing an inverse $f^{-1}$ .

I will work backwards on scratch paper and figure out a formula for the inverse. Then I'll prove that my formula works.

Scratch work: Suppose the inverse $g: \real^2 \to \real^2$ is

$$g(u, v) = (x, y).$$

Now f and g are supposed to be inverses, so $f[g(u, v)] = (u, v)$ . So

$$\eqalign{ f[g(u, v)] & = f(x, y) \cr (u, v) & = (2 x + y^3, x + 1) \cr}$$

This gives

$$u = 2 x + y^3 \quad\hbox{and}\quad v = x + 1.$$

I want the formula for $g(u, v) = (x, y)$ , which means I want to find x and y in terms of u and v. Thus, I solve the two equations above simultaneously. From $v = x + 1$ , I get

$$x = v - 1.$$

That's x. Now plug this into $u = 2 x + y^3$ and solve for y:

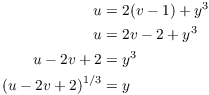
$$\eqalign{ u & = 2(v - 1) + y^3 \cr u & = 2 v - 2 + y^3 \cr u - 2 v + 2 & = y^3 \cr (u - 2 v + 2)^{1/3} & = y \cr}$$

Thus, the formula for g is

$$g(u, v) = (x, y) = (v - 1, (u - 2 v + 2)^{1/3}).$$

That ends the scratch work, and I do the "real proof".

Let $g(u, v) = (x, y) = (v - 1, (u - 2 v + 2)^{1/3})$ . I must show that

$$g(f(x, y)) = (x, y) \quad\hbox{and}\quad f(g(u, v)) = (u, v).$$

First,

$$\eqalign{ g(f(x, y)) & = g\left(2 x + y^3, x + 1\right) \cr & = ((x + 1) - 1, [(2 x + y^3) - 2(x + 1) + 2]^{1/3}) \cr & = (x, (2 x + y^3 - 2 x - 2 + 2)^{1/3}) \cr & = (x, (y^3)^{1/3}) \cr & = (x, y) \cr}$$

Before doing the next equation, let's explain the second equality. "$g\left(2 x + y^3, x + 1\right)$ " means to plug $2 x + y^3$ in for y and $x + 1$ in for v in the definition $g(u, v) = (x, y) = (v - 1, (u - 2 v + 2)^{1/3})$ . Check carefully for yourself that we did that.

Another important point: When you compute $g(f(x, y))$ , there should only be x's and y's in your work. You can't have any u's and v's, because u and v aren't "global variables" --- they don't exist outside of the definition of $g(u, v)$ .

Please look at the computation above and read the last paragraph again, because it is easy to make the mistake you're being warned about!

Next,

$$\eqalign{ f(g(u, v)) & = f(v - 1, (u - 2 v + 2)^{1/3}) \cr & = (2(v - 1) + [(u - 2 v + 2)^{1/3}]^3, (v - 1) + 1) \cr & = (2 v - 2 + u - 2 v + 2, v) \cr & = (u, v) \cr}$$

As in the previous derivation, I got the second equality by plugging $v - 1$ in for x and $(u - 2 v + 2)^{1/3}$ in for y in $f(x, y) = (2 x + y^3, x + 1)$ .

By analogy with the first derivation, when you do $f(g(u, v))$ , there should only be u's and v's in your work --- you can't have any x's and y's.

The two equations above show that f and g are inverses. Therefore, f is bijective.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga