Infinite Unions and Intersections

The set constructions I've considered so far --- things like $A \cup B$ , $\overline{C}$ , $D \cap E$ --- have involved finite numbers of sets. It's often necessary to work with infinite collections of sets, and to do this, you need a way of naming them and keeping track of them.

Definition. Let I be a set. A collection of sets indexed by I consists of a collection of sets $S_i$ , one set $S_i$ for each element $i \in I$ .

You could make this more precise by defining a collection of sets indexed by I to be a function from I to the class of all sets. I'll stick with this informal definition, since it won't cause us any difficulties in what we do.

Let $I = \{1, 2, 3, 4\}$ . A collection of sets indexed by I consists of four sets $S_1$ , $S_2$ , $S_3$ , and $S_4$ . For example,

$$S_1 = \{1, 2, 3\}, \quad S_2 = \{a, b, c\}, \quad S_3 = \real, \quad S_4 = \{1, 2, 3\}.$$

Note that $S_1 = S_3$ ; some of the sets in the collection may be identical.

Here's another collection of sets indexed by I:

$$S_1 = \emptyset, \quad S_2 = \integer, \quad S_3 = \{\pi, e\}, \quad S_4 = \{\hbox{pepperoni}, \hbox{sausage}\}.$$

This would not be very interesting if I were only considering finite collections of sets. Here are some infinite collections of sets.

Let $I = \natural = \{1, 2, 3, \ldots\}$ . A collection of sets indexed by I is an infinite collection of sets $S_1$ , $S_2$ , $S_3$ , $S_4$ , ....

Here is a collection of sets indexed by $\natural$ :

$$S_1 = (0, 1), \quad S_2 = \left(0, \dfrac{1}{2}\right), \quad S_3 = \left(0, \dfrac{1}{3}\right), \ldots.$$

In general, if n is a positive integer, then $S_n = \left(0, \dfrac{1}{n}\right)$ .

Here's another collection of sets indexed by $\natural$ :

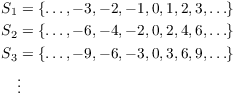
$$\eqalign{ S_1 & = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\} \cr S_2 & = \{\ldots, -6, -4, -2, 0, 2, 4, 6, \ldots\} \cr S_3 & = \{\ldots, -9, -6, -3, 0, 3, 6, 9, \ldots\} \cr & \vdots \cr}$$

In general, $S_n$ consists of the integers which are divisible by n.

Now let $I = \real$ . Here's a collection of sets indexed by I:

$$S_x = \{x, -x\} \quad\hbox{for}\quad x \in \real.$$

For instance, I have sets $S_3$ , $S_{-117/13}$ , $S_{\pi}$ , and so on, one for every real number.

Since $\real$ is uncountable, I can't list the sets in this collection the way I could list collections of sets indexed by $\natural$ .

Here are a couple of the sets:

$$S_{\sqrt{2}} = \{\sqrt{2}, -\sqrt{2}\}, \quad S_{42} = \{42, -42\}.$$

Here's another collection of sets indexed by $\real$ :

$$S_x = [x, \infty) \quad\hbox{for}\quad x \in \real.$$

Each set in this collection is an interval consisting of all real numbers greater than or equal to x. So, for example,

$$S_1 = [1, \infty), \quad S_{\pi} = [\pi, \infty).$$

Definition. Let I be a set, and let $\{S_i\}$ be a collection of sets indexed by I.

(a) The union $\bigcup_{i\in I} S_i$ of the $S_i$ is the set

$$\bigcup_{i\in I} S_i = \{s \mid s \in S_i \quad\hbox{for some}\quad i \in I\}.$$

(b) The intersection $\bigcap_{i\in I} S_i$ of the $S_i$ is the set

$$\bigcap_{i\in I} S_i = \{s \mid s \in S_i \quad\hbox{for all}\quad i \in I\}.$$

Remark. For a collection of sets $S_1$ , $S_2$ , $S_3$ , ... indexed by the natural numbers, you usually write the union and intersection this way:

$$\bigcup_{n = 1}^\infty S_n \quad\hbox{and}\quad \bigcap_{n = 1}^\infty S_n.$$

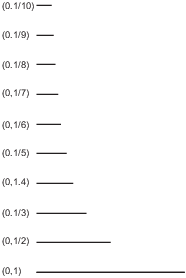
Example. Consider the following collection of sets indexed by $\natural$ :

$$S_1 = (0,1), \quad S_2 = \left(0,\dfrac{1}{2}\right), \quad S_3 = \left(0,\dfrac{1}{3}\right), \ldots, S_n = \left(0,\dfrac{1}{n}\right), \ldots.$$

Prove:

(a) $\displaystyle \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right) = (0, 1)$ .

(b) $\displaystyle \bigcap_{n = 1}^\infty \left(0, \dfrac{1}{n}\right) = \emptyset$ .

The collection of intervals is shown below. They actually lie on top of one another on the x-axis; I've "pulled them up" so you can see them separately.

$$\hbox{\epsfysize=2.5 in \epsffile{infinite-unions-and-intersections-1.eps}}$$

(a) I will show each set is contained in the other. Let $\displaystyle x \in \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ . Then $x \in \left(0, \dfrac{1}{n}\right)$ for some $n > 1$ . This means that $0 < x < \dfrac{1}{n}$ .

Now $n > 1$ implies $\dfrac{1}{n} < 1$ , so $0 < x < 1$ . Hence, $x \in (0, 1)$ .

This proves that $\displaystyle \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right) \subset (0, 1)$ .

Conversely, suppose $x \in (0, 1)$ . Now $S_1 = (0, 1)$ , so by the definition of union, $\displaystyle x \in \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ . This proves that $\displaystyle (0, 1) \subset \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ .

Hence, $\displaystyle \bigcup_{n = 1}^\infty \left(0, \dfrac{1}{n}\right) = (0, 1)$ .

(b) Since the empty set is a subset of any set, I have $\displaystyle \emptyset \subset \bigcap_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ .

The opposite inclusion is $\displaystyle \bigcap_{n = 1}^\infty \left(0, \dfrac{1}{n}\right) \subset \emptyset$ . To show this means to show that $\displaystyle \bigcap_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ contains no elements. I'll give a proof by contradiction.

Suppose on the contrary that $\displaystyle c \in \bigcap_{n = 1}^\infty \left(0, \dfrac{1}{n}\right)$ . By the definition of intersection, this means that $c \in \left(0, \dfrac{1}{n}\right)$ for every positive integer n.

Note that

$$\lim_{n \to \infty} \dfrac{1}{n} = 0.$$

In the limit definition, choose $\epsilon = c$ . Then there is a number M such that for all $n > M$ , I have

$$c = \epsilon > \left|\dfrac{1}{n} - 0\right| = \dfrac{1}{n}.$$

Choose a positive integer n such that $n > M$ . Then

$$0 < \dfrac{1}{n} < c.$$

But this means that $c \notin \left(0, \dfrac{1}{n}\right)$ , contradicting the fact that $c \in \left(0, \dfrac{1}{n}\right)$ for every positive integer n.

This shows that there is no such element c, so the intersection is empty.

Example. Prove that $\displaystyle \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right] = [0, 1)$ .

First, I'll show that the left side is contained in the right side. Let $\displaystyle x \in \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right]$ . I have to show that $x \in [0, 1)$ .

Since $\displaystyle x \in \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right]$ , I know that $x \in \left[0, \dfrac{n}{n + 1}\right]$ for some $n \ge 1$ . This means that

$$0 \le x \le \dfrac{n}{n + 1}.$$

But

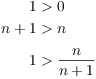
$$\eqalign{ 1 & > 0 \cr n + 1 & > n \cr \noalign{\vskip2pt} 1 & > \dfrac{n}{n + 1} \cr}$$

Therefore, $0 \le x < 1$ . This means that $x \in [0, 1)$ . Hence, $\displaystyle \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right] \subset [0, 1)$ .

Next, I'll show that the right side is contained in the left side. Suppose $x \in [0, 1)$ . I have to show that $\displaystyle x \in \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right]$ .

Since $x \in [0, 1)$ , I have $0 \le x < 1$ . Note that

$$\lim_{n \to \infty} \dfrac{n}{n + 1} = 1.$$

I'll pause to give a picture of what I'll do next. The idea is that since $\dfrac{n}{n + 1}$ is approaching 1, and since $x < 1$ , eventually the $\dfrac{n}{n + 1}$ terms must become larger than x:

$$\hbox{\epsfxsize=2in \epsffile{infinite-unions-and-intersections-2.eps}}$$

Intuitively, if all the $\dfrac{n}{n + 1}$ 's stayed to the left of x, then their limit couldn't be greater than x, so the limit couldn't be 1.

Continuing the proof, in the limit definition, let $\epsilon = 1 - x$ . Then there is a number M such that if $n > M$ ,

$$1 - x = \epsilon > \left|\dfrac{n}{n + 1} - 1\right|.$$

Since $\dfrac{n}{n + 1} < 1$ , the absolute value becomes

$$-\left(\dfrac{n}{n + 1} - 1\right) = 1 - \dfrac{n}{n + 1}.$$

The inequality above becomes

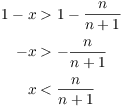
$$\eqalign{ 1 - x & > 1 - \dfrac{n}{n + 1} \cr \noalign{\vskip2pt} -x & > -\dfrac{n}{n + 1} \cr \noalign{\vskip2pt} x & < \dfrac{n}{n + 1} \cr}$$

That is, for some n I have $x < \dfrac{n}{n + 1}$ . Since I already know $x \ge 0$ , I have

$$0 \le x < \dfrac{n}{n + 1}.$$

This means that $x \in \left[0, \dfrac{n}{n + 1}\right)$ . By the definition of union, $\displaystyle x \in \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right]$ . Therefore, $\displaystyle [0, 1) \subset \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right]$ .

Since I've proved both inclusions, I have $\displaystyle \bigcup_{n = 1}^\infty \left[0, \dfrac{n}{n + 1}\right] = [0, 1)$ .

Example. Prove that

$$\bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right] = [1, 3].$$

I'll show that each of the sets $\displaystyle \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right]$ and $[1, 3]$ is contained in the other.

I'll do the easy inclusion first. Let $x \in [1, 3]$ . Then $1 \le x \le 3$ .

For all $n \ge 1$ , I have $3 < 3 + \dfrac{1}{n}$ . Hence,

$$1 \le x \le 3 < 3 + \dfrac{1}{n}.$$

Therefore, $x \in \left[1, 3 + \dfrac{1}{n}\right]$ for all $n \ge 1$ . By definition of intersection, $x \in \displaystyle \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right]$ .

Thus, $\displaystyle [1, 3] \subset \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right]$ .

Next, let $\displaystyle x \in \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right]$ . This means that $x \in \left[1, 3 + \dfrac{1}{n}\right]$ for all $n \ge 1$ --- that is,

$$1 \le x \le 3 + \dfrac{1}{n} \quad\hbox{for all}\quad n \ge 1.$$

I have to show that $x \le 3$ . Suppose on the contrary that $x > 3$ .

Note that

$$\lim_{n \to \infty} \left(3 + \dfrac{1}{n}\right) = 3.$$

In the limit definition, let $\epsilon = x - 3$ . Then there is a number M such that if $n > M$ ,

$$\epsilon = x - 3 > \left|3 + \dfrac{1}{n} - 3\right| = \left|\dfrac{1}{n}\right| = \dfrac{1}{n}.$$

(I can drop the absolute values because n is positive.)

For any n such that $n > M$ , I have

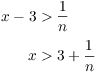
$$\eqalign{ x - 3 & > \dfrac{1}{n} \cr \noalign{\vskip2pt} x & > 3 + \dfrac{1}{n} \cr}$$

But this contradicts the fact that $1 \le x \le 3 + \dfrac{1}{n}$ for all $n \ge 1$ .

Intuitively, since $\displaystyle \lim_{n \to \infty} \left(3 + \dfrac{1}{n}\right) = 3$ , if $x > 3$ then eventually the $3 + \dfrac{1}{n}$ 's must shrink to the left of x.

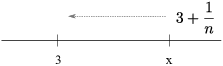
$$\hbox{\epsfxsize=2in \epsffile{infinite-unions-and-intersections-3.eps}}$$

If all of them stayed to the right of x, the limit would be greater than or equal to x, so it couldn't be 3.

This proves by contradiction that $x \le 3$ . Since I already know that $1 \le x$ , I have $1 \le x \le 3$ , or $x \in [1, 3]$ .

Thus, $\displaystyle \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right] \subset [1, 3]$ .

Together with the first inclusion, this proves that $\displaystyle \bigcap_{n = 1}^\infty \left[1, 3 + \dfrac{1}{n}\right] = [1, 3]$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga