Limits at Infinity

In this section, I'll discuss proofs for limits of the form $\displaystyle \lim_{x \to \infty} f(x)$ . They are like $\epsilon-\delta$ proofs, though the setup and algebra are a little different.

Recall that $\displaystyle \lim_{x \to c} f(x) = L$ means that for every $\epsilon > 0$ , there is a $\delta$ such that if

$\delta > |x - c| > 0, \quad\hbox{then}\quad \epsilon > |f(x) - L|.$

Definition. $\displaystyle \lim_{x \to \infty} f(x) = L$ means that for every $\epsilon > 0$ , there is an M such that if

$x > M , \quad\hbox{then}\quad \epsilon > |f(x) - L|.$

In other words, I can make as close to L as I please by making x sufficiently large.

Remarks. Limits at infinity often occur as limits of sequences, such as

$\dfrac{1}{2}, \quad \dfrac{1}{3}, \quad \dfrac{1}{4}, \ldots, \dfrac{1}{n}, \ldots.$

In this case, $\displaystyle \lim_{n \to \infty} \dfrac{1}{n} = 0$ . I won't make a distinction between the limit at infinity of a sequence and the limit at infinity of a function; the proofs you do are essentially the same in both cases.

There is s similar definition for $\displaystyle \lim_{x \to -\infty} f(x) = L$ , and the proofs are similar as well. I'll stick to $\displaystyle \lim_{x \to \infty} f(x)$ here.

Example. Prove that $\displaystyle \lim_{n \to \infty} \dfrac{1}{n} = 0$ .

As with $\epsilon-\delta$ proofs, I do some scratch work, working backwards from what I want. Then I write the "real proof" in the forward direction.

Scratch work. I want

$\epsilon > \left|\dfrac{1}{n} - 0\right| = \left|\dfrac{1}{n}\right| = \dfrac{1}{n}.$

I want to drop the absolute values, so I'll assume . Rearranging the inequality, I get $n > \dfrac{1}{\epsilon}$ .

Here's the real proof. Let $\epsilon > 0$ . Set $M = \dfrac{1}{\epsilon}$ . Since $\epsilon > 0$ , I have $M = \dfrac{1}{\epsilon} > 0$ . Suppose . Then , and

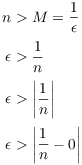
$\eqalign{ n & > M = \dfrac{1}{\epsilon} \cr \noalign{\vskip2 pt} \epsilon & > \dfrac{1}{n} \cr \noalign{\vskip2 pt} \epsilon & > \left|\dfrac{1}{n}\right| \cr \noalign{\vskip2 pt} \epsilon & > \left|\dfrac{1}{n} - 0\right| \cr}$

This proves that $\displaystyle \lim_{n \to \infty} \dfrac{1}{n} = 0$ .

Example. Prove that $\displaystyle \lim_{x \to \infty} \dfrac{6 x + 1}{2 x + 1} = 3$ .

Scratch work. I want

$\epsilon > \left|\dfrac{6 x + 1}{2 x + 1} - 3\right| = \left|\dfrac{6 x + 1 - 3(2 x + 1)}{2 x + 1}\right| = \left|\dfrac{-2}{2 x + 1}\right| = \left|\dfrac{2}{2 x + 1}\right| = \dfrac{2}{2 x + 1}.$

In order to drop the absolute values, I need to assume .

Rearrange the inequality:

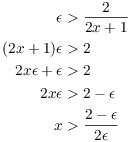
$\eqalign{ \epsilon & > \dfrac{2}{2 x + 1} \cr (2 x + 1)\epsilon & > 2 \cr 2 x \epsilon + \epsilon & > 2 \cr 2 x \epsilon & > 2 - \epsilon \cr x & > \dfrac{2 - \epsilon}{2 \epsilon} \cr}$

Here's the real proof. Let $\epsilon > 0$ . Set $M = \max\left(0, \dfrac{2 - \epsilon}{2 \epsilon}\right)$ . If , then and $x > \dfrac{2 - \epsilon}{2 \epsilon}$ . So

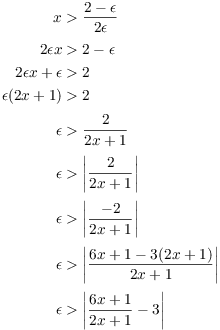
$\eqalign{ x & > \dfrac{2 - \epsilon}{2 \epsilon} \cr \noalign{\vskip2pt} 2 \epsilon x & > 2 - \epsilon \cr 2 \epsilon x + \epsilon & > 2 \cr \epsilon (2 x + 1) & > 2 \cr \noalign{\vskip2pt} \epsilon & > \dfrac{2}{2 x + 1} \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{2}{2 x + 1}\right| \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{-2}{2 x + 1}\right| \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{6 x + 1 - 3(2 x + 1)}{2 x + 1}\right| \cr \noalign{\vskip2pt} \epsilon & > \left|\dfrac{6 x + 1}{2 x + 1} - 3\right| \cr}$

Therefore,

$\lim_{x \to \infty} \dfrac{6 x + 1}{2 x + 1} = 3.\quad\halmos$

Note that the expression $\dfrac{2 - \epsilon}{2 \epsilon}$ would be negative if $\epsilon > 2$ . So I took M to be the max of 0 and $\dfrac{2 - \epsilon}{2 \epsilon}$ to ensure that if , then x would be positive. Now you actually need to be positive in order to put on the absolute values, and if $x > -\dfrac{1}{2}$ . It isn't hard to prove that $\dfrac{2 - \epsilon}{2 \epsilon} > -\dfrac{1}{2}$ , so in fact I don't need to take the max with 0 --- provided that I'm willing to prove that $\dfrac{2 - \epsilon}{2 \epsilon} > -\dfrac{1}{2}$ . I decided to take the easy way out!

Example. Prove that $\displaystyle \lim_{n \to \infty} (-1)^n$ is undefined.

I'll use proof by contradiction. Suppose that

$\lim_{n \to \infty} (-1)^n = L.$

Taking $\epsilon = \dfrac{1}{2}$ in the definition, I can find M such that if , then $\dfrac{1}{2} > |(-1)^n - L|$ .

Choose p to be an even number greater than M. Then

$\dfrac{1}{2} > |(-1)^p - L| = |1 - L|.$

This says that the distance from L to 1 is less than $\dfrac{1}{2}$ , so

$\dfrac{1}{2} < L < \dfrac{3}{2}.$

Choose q to be an odd number greater than M. Then

$\dfrac{1}{2} > |(-1)^q - L| = |-1 - L|.$

This says that the distance from L to -1 is less than $\dfrac{1}{2}$ , so

$-\dfrac{3}{2} < L < -\dfrac{1}{2}.$

This is a contradiction, since L can't be in $\left(\dfrac{1}{2}, \dfrac{3}{2}\right)$ and in $\left(-\dfrac{3}{2}, -\dfrac{1}{2}\right)$ at the same time.

Hence, $\displaystyle \lim_{n \to \infty} (-1)^n$ is undefined.

Contact information

Bruce Ikenaga's Home Page