Modular Arithmetic

Definiton. Let a, b, and m be integers. a is congruent to b mod m if $m \mid a - b$ ; that is, if

$a - b = k m \hbox{ for some integer } k.$

Notation: $a = b\mod{m}$ means that a is congruent to b mod m. m is called the modulus of the congruence; I will almost always work with positive moduli.

Note that $a = 0\mod{m}$ if and only if $m \mid a$ . Thus, modular arithmetic gives you another way of dealing with divisibility relations.

For example:

$101 = 3 \mod{2}$ because $2 \mid 101 - 3 = 98$ .

$19 = -17 \mod{12}$ because $12 \mid 19 - (-17) = 36$ .

Proposition. Congruence mod m is an equivalence relation:

(a) ( Reflexivity) $a = a \mod{m}$ for all a.

(b) ( Symmetry) If $a = b \mod{m}$ , then $b = a \mod{m}$ .

Proof. Since $m \mid 0 = a - a$ , it follows that $a = a \mod{m}$ .

Suppose $a = b \mod{m}$ . Then $m \mid a - b$ , so $m \mid b - a$ . Hence, $b = a \mod{m}$ .

Suppose $a = b \mod{m}$ and $b = c \mod{m}$ . Then there are integers j and k such that

$a - b = j m, \quad b - c = k m.$

Add the two equations:

This implies that $a = c\mod{m}$ .

Example. (a) List the elements of the equivalence classes relative to congruence mod 3.

(b) Using 0, 1, and 2 to represent these equivalence classes, construct addition and multiplication tables mod 3.

(a) The equivalence classes are the 3 congruence classes:

$\{\ldots, -3, 0, 3, 6, \ldots\}, \quad \{\ldots -4, -1, 2, 5, \ldots\}, \quad \{\ldots -5, -2, 1, 4, \ldots\}.$

Each integer belongs to exactly one of these classes. Two integers in a given class are congruent mod 3.

(If you know some group theory, you probably recognize this as constructing $\integer_3$ from $\integer$ .)

(b)

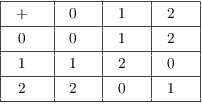
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

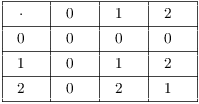
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

For example, , because as integers, and the congruence class of 3 is represented by 0. Likewise, $2 \cdot 2 = 4$ as integers, and the congruence class of 4 is represented by 1.

I could have chosen different representatives for the classes --- say 3, -4, and 4. A choice of representatives, one from each class, is called a complete system of residues mod 3. But working mod 3 it's natural to use the numbers 0, 1, and 2 as representatives --- and in general, if I'm working mod n, the obvious choice of representatives is the set $\{0, 1, 2, \ldots, n - 1\}$ . This set is called the standard residue system mod n, and it is the set of representatives I'll usually use. Thus, the standard residue system mod 6 is $\{0, 1, 2, 3, 4, 5\}$ .

Theorem. Suppose $a = b\mod{m}$ and $c = d \mod{m}$ . Then:

(a) $a + c = b + d \mod{m}$ and $a - c = b - d \mod{m}$ .

(b) $a c = b d \mod{m}$ .

Proof. I'll prove the first congruence as an example. Suppose $a = b \mod{m}$ and $c = d \mod{m}$ . Then and for some $j, k \in \integer$ , so

This implies that $a + c = b + d \mod{m}$ .

Example. Solve the congruence

$7 x + 1 = 2 (2 x + 8) \mod{11}.$

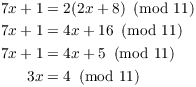
$\eqalign{ 7 x + 1 & = 2 (2 x + 8) \mod{11} \cr 7 x + 1 & = 4 x + 16 \mod{11} \cr 7 x + 1 & = 4 x + 5 \mod{11} \cr 3 x & = 4 \mod{11} \cr}$

There are no "fractions" mod 11. I want to divide by 3, and to do this I need to multiply by the multiplicative inverse of 3. So I need a number k such that $k \cdot 3 = 1 \mod{11}$ . A systematic way of finding such a number is to use the Extended Euclidean algorithm. In this case, I just use trial and error. Obviously, and won't work, so I'll start at :

$2 \cdot 3 = 6 \mod{11}, \quad 3 \cdot 3 = 9 \mod{11}, \quad 4 \cdot 3 = 12 = 1 \mod{11}.$

Thus, I need to multiply the equation by 4:

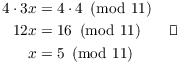
$\eqalign{ 4 \cdot 3 x & = 4 \cdot 4 \mod{11} \cr 12 x & = 16 \mod{11} \cr x & = 5 \mod{11} \cr} \quad\halmos$

Definition. x and y are multiplicative inverses mod n if $x y = 1 \mod{n}$ .

Notation: $x = y^{-1} \mod{n}$ or $y = x^{-1} \mod{n}$ . Do not use fractions.

Example. (a) Find $6^{-1} \mod{17}$ .

(b) Prove that 6 does not have a multiplicative inverse mod 8.

(a) $6 \cdot 3 = 18 = 1 \mod{17}$ , so $6^{-1} = 3 \mod{17}$ .

(b) Suppose $6 x = 1 \mod{8}$ . Then

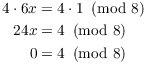
$\eqalign{ 4 \cdot 6 x & = 4 \cdot 1 \mod{8} \cr 24 x & = 4 \mod{8} \cr 0 & = 4 \mod{8} \cr}$

This contradiction shows that 6 does not have a multiplicative inverse mod 8.

Example. Reduce $996 \cdot 997 \cdot 998 \cdot 999 \mod{1000}$ to a number in $\{0, 1, \ldots, 999\}$ .

$996 \cdot 997 \cdot 998 \cdot 999 = (-4)(-3)(-2)(-1) = 24 \mod{1000}.\quad\halmos$

Example. Reduce $99^{10} \mod{7}$ to a number in $\{0, 1, 2, 3, 4, 5, 6\}$ .

$99 = 1\mod{7}$ , so

$99^{10} = 1^{10} = 1 \mod{7}.\quad\halmos$

Example. Show that if p is prime, then

$(x + y)^p = x^p + y^p \mod{p}.$

By the Binomial Theorem,

$(x + y)^p = \sum_{i=0}^p {p \choose i} x^i y^{p-i}.$

A typical coefficient $\displaystyle {p \choose i} = \dfrac{p!}{i!\, (p - i)!}$ is divisible by p for $i \ne 0, p$ . So going mod p, the only terms that remain are and .

For example

$(x + y)^2 = x^2 + y^2 \mod{2} \quad\hbox{and}\quad (x + y)^3 = x^3 + y^3 \mod{3}.$

The result is not true if the modulus is not prime. For example,

$(1 + 1)^4 = 0 \mod{4}, \quad\hbox{but}\quad 1^4 + 1^4 = 2 \mod{4}.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page