Order Relations

A partial order on a set is, roughly speaking, a relation that behaves like the relation $\le$ on $\real$ .

Definition. Let X be a set, and let $\sim$ be a relation on X. $\sim$ is a partial order if:

(a) (Reflexive) For all $x \in X$ , $x \sim x$ .

(b) (Antisymmetric) For all $x, y \in X$ , if $x \sim y$ and $y \sim x$ , then $x = y$ .

(c) (Transitive) For all $x, y, z \in X$ , if $x \sim y$ and $y \sim z$ , then $x \sim z$ .

Example. For each relation, check each axiom for a partial order. If the axiom holds, prove it. If the axiom does not hold, give a specific counterexample.

(a) The relation $\le$ on $\real$ .

(b) The relation $<$ on $\real$ .

(a) For all $x \in \real$ , $x \le x$ : Reflexivity holds.

For all $x, y \in \real$ , if $x \le y$ and $y \le x$ , then $x = y$ : Antisymmetry holds.

For all $x, y, z \in \real$ , if $x \le y$ and $y \le z$ , then $x \le z$ : Transitivity holds.

Thus, $\le$ is a partial order.

(b) For no x is it true that $x < x$ , so reflexivity fails.

Antisymmetry would say: If $x < y$ and $y < x$ , then $x = y$ . However, for no $x, y \in \real$ is it true that $x < y$ and $y < x$ . Therefore, the first part of the conditional is false, and the conditional is true. Thus, antisymmetry is vacuously true.

If $x < y$ and $y < z$ , then $x < z$ . Therefore, transitivity holds.

Hence, $<$ is not a partial order.

Example. Let X be a set and let $\powerset(X)$ be the power set of X --- i.e. the set of all subsets of X. Show that the relation of set inclusion is a partial order on $\powerset(X)$ .

Subsets A and B of X are related under set inclusion if $A \subset B$ .

If $A \subset X$ , then $A \subset A$ . The relation is reflexive.

Suppose $A, B \subset X$ . If $A \subset B$ and $B \subset A$ , then by definition of set equality, $A = B$ . The relation is symmetric.

Finally, suppose $A, B, C \subset X$ . If $A \subset B$ and $B \subset C$ , then $A \subset C$ . (You can write out the easy proof using elements.) The relation is transitive.

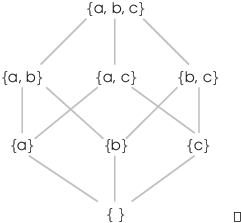
Here's a particular example. Let $X = \{a, b, c\}$ . This is a picture of the set inclusion relation on $\powerset(X)$ :

$$\hbox{\epsfysize=2in \epsffile{order-relations-1.eps}}\quad\halmos$$

Definition. Let $(X, \le)$ be a partially ordered set. The lexicographic order (or dictionary order) on $X \times X$ is defined as follows: $(x_1, y_1) \sim (x_2, y_2)$ means that

(a) $x_1 < x_2$ , or

(b) $x_1 = x_2$ and $y_1 \le y_2$ .

Note that $(x_1, y_1) \sim (x_2, y_2)$ implies $x_1 \le x_2$ .

You can extend the definition to two different partially ordered sets X and Y, or a sequence $X_1$ , $X_2$ , ..., $X_n$ of partially ordered sets in the same way. The name dictionary order comes from the fact that it describes the way words are ordered alphabetically in a dictionary. For instance, "aardvark" comes before "banana" because "a" comes before "b". If the first letters are the same, as with "mystery" and "meat", then you look at the second letters: "e" comes before "y", so "meat" comes before "mystery".

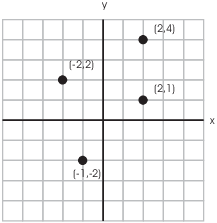
$$\hbox{\epsfysize=2in \epsffile{order-relations-2.eps}}$$

In the picture above, $(-2, 2) \sim (-1, -2)$ , because $-2 < -1$ . And $(2, 1) \sim (2, 4)$ because the x-coordinates are equal and $1 < 4$ .

Proposition. The lexicographic order on $X \times X$ is a partial order.

Proof. First, $(x, y) \sim (x, y)$ , since $x = x$ and $y \le y$ . $\sim$ is reflexive.

Next, suppose $(x_1, y_1) \sim (x_2, y_2)$ and $(x_2, y_2) \sim (x_1, y_1)$ . Now $(x_1, y_1) \sim (x_2, y_2)$ means that either $x_1 < x_2$ or $x_1 = x_2$ . The first case $x_1 < x_2$ is impossible, since this would contradict $(x_2, y_2) \sim (x_1, y_1)$ . Therefore, $x_1 = x_2$ . Then $(x_1, y_1) \sim (x_2, y_2)$ implies $y_1 \le y_2$ and $(x_2, y_2) \sim (x_1, y_1)$ implies $y_2 \le y_1$ . Hence, $y_1 = y_2$ . Therefore, $(x_1, y_1) = (x_2, y_2)$ . $\sim$ is antisymmetric.

Finally, suppose $(x_1, y_1) \sim (x_2, y_2)$ and $(x_2, y_2) \sim (x_3, y_3)$ . To keep things organized, I'll consider the four cases.

(a) If $x_1 < x_2$ and $x_2 < x_3$ , then $x_1 < x_3$ , so $(x_1, y_1) \sim (x_3, y_3)$ .

(b) If $x_1 < x_2$ and $x_2 = x_3$ , then $x_1 < x_3$ , so $(x_1, y_1) \sim (x_3, y_3)$ .

(c) If $x_1 = x_2$ and $x_2 < x_3$ , then $x_1 < x_3$ , so $(x_1, y_1) \sim (x_3, y_3)$ .

(d) If $x_1 = x_2$ and $x_2 = x_3$ , then $y_1 \le y_2$ and $y_2 \le y_3$ . This implies $x_1 = x_3$ and $y_1 \le y_3$ , so $(x_1, y_1) \sim (x_3, y_3)$ .

Hence, $\sim$ is transitive, and this completes the proof that $\sim$ is a partial order.

A common mistake in working with partial orders --- and in real life --- consists of assuming that if you have two things, then one must be bigger than the other. When this is true about two things, the things are said to be comparable. However, in an arbitrary partially ordered set, some pairs of elements are comparable and some are not.

Definition. Let $\sim$ be a relation on a set X. x and y in X are comparable if either $x \sim y$ or $y \sim x$ .

Here's a pictorial example to illustrate the idea. You can sometimes describe an order relation by drawing a graph like the one below:

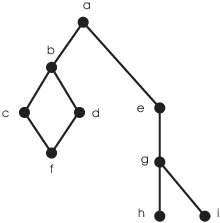
$$\hbox{\epsfysize=2in \epsffile{order-relations-3.eps}}$$

This picture shows a relation $\sim$ on the set

$$S = \{a, b, c, d, e, f, g, h, i\}.$$

Two elements are comparable if they're joining by a sequence of edges that goes upward "without reversing direction". (Think of "bigger" elements being above and "smaller" elements being below.) It's also understood that every element satisfies $x \sim x$ .

For example, $f \sim c$ , since there's an upward segment connecting f to c. And $f \sim a$ , since there's an upward path of segments $f \to c \to b \to a$ connecting f to a.

On the other hand, there are elements which are not comparable. For example, d and e are not comparable, because there is no upward path of segments connecting one to the other. Likewise, $g \sim h$ and $g \sim i$ , but h and i are not comparable.

Notice that a is comparable to every element of the set, and that $x \sim a$ for all $x \in S$ .

Definition. Let X be a partially ordered set.

(a) An element $x \in X$ which is comparable to every other element of X and satisfies $x \ge y$ for all $y \in X$ is the largest element of the set.

(b) An element $x \in X$ which is comparable to every other element of X and satisfies $x \le y$ for all $y \in X$ is the smallest element of the set.

In some cases, we only care that an element be "bigger than" or "smaller than" elements to which it is comparable.

Definition. Let X be a partially ordered set. If an element x satisfies $x \ge y$ for all y to which it is comparable, then x is a maximal element. Likewise, if an element x satisfies $x \le y$ for all y to which it is comparable, then x is a minimal element.

Note that a largest or smallest element, if it exists, is unique. On the other hand, there may be many maximal or minimal elements.

Example. Define a relation $\sim$ on $\real$ by

$$x \sim y \quad\hbox{means}\quad x^3 - 4 x \le y^3 - 4 y.$$

Check each axiom for a partial order. If the axiom holds, prove it. If the axiom does not hold, give a specific counterexample.

$x^3 - 4 x \le x^3 - 4 x$ for all $x \in \real$ , so $x \sim x$ for all $x \in \real$ . Therefore, $\sim$ is reflexive.

Suppose $x \sim y$ and $y \sim x$ . Is is true that $x = y$ ?

$2 \sim -2$ , since $2^3 - 4\cdot 2 \le (-2)^3 - 4\cdot (-2)$ . Likewise, $-2 \sim 2$ , since $(-2)^3 - 4\cdot (-2) \le 2^3 - 4\cdot 2$ . But $2 \ne -2$ , so $\sim$ is not antisymmetric.

Finally, suppose $x \sim y$ and $y \sim z$ . This means that $x^3 - 4 x \le y^3 - 4 y$ and $y^3 - 4 y \le z^3 - 4 z$ . Hence, $x^3 - 4 x \le z^3 - 4 z$ . Therefore, $x \sim z$ , so $\sim$ is transitive.

Example. Define a relation $\sim$ on $\real^2$ by

$$(a, b) \sim (c, d) \quad\hbox{means}\quad |a b| \ge |c d|.$$

Check each axiom for a partial order. If the axiom holds, prove it. If the axiom does not hold, give a specific counterexample.

Since $|a b| \ge |a b|$ for all $(a, b) \in \real^2$ , it follows that $(a, b) \sim (a, b)$ for all $(a, b) \in \real^2$ . Therefore, $\sim$ is reflexive.

$(1, 2) \sim (-1, 2)$ , since $|1 \cdot 2| \ge |(-1) \cdot 2|$ . Likewise, $(-1, 2) \sim (1, 2)$ , since $|(-1) \cdot 2| \ge |1 \cdot 2|$ . However, $(1, 2) \ne (-1, 2)$ . Therefore, $\sim$ is not antisymmetric.

Finally, suppose $(a, b) \sim (c, d)$ and $(c, d) \sim (e, f)$ . Then $|a b| \ge |c d|$ and $|c d| \ge |e f|$ . Hence, $|a b| \ge |e f|$ . Therefore, $(a, b) \sim (e, f)$ . Hence, $\sim$ is transitive.

Definition. A relation $\sim$ on a set X is a total order if:

(a) (Trichotomy) For all $x, y \in X$ , exactly one of the following holds: $x \sim y$ , $y \sim x$ , or $x = y$ .

(b) (Transitivity) For all $x, y, z \in X$ , if $x \sim y$ and $y \sim z$ , then $x \sim z$ .

The usual less than relation $<$ is a total order on $\integer$ , on $\rational$ , and on $\real$ . Likewise, you can use the total order relation on $\integer$ to define a lexicographic order on $\integer \times \integer$ which is a total order. Specifically, define a total order $\sim$ on $\integer \times \integer$ as follows: $(x_1, y_1) \sim (x_2, y_2)$ means that

(a) $x_1 < x_2$ , or

(b) $x_1 = x_2$ and $y_1 < y_2$ .

You can check that the axioms for a total order hold.

Example. Consider the relation defined by the graph below:

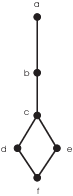
$$\hbox{\epsfysize=1.75in \epsffile{order-relations-4.eps}}$$

Thus, $x < y$ means that $x \ne y$ , and there is an upward path of segments from x to y.

Is this relation a total order? You can check cases, using the picture, that the relation is transitive. (This amounts to saying that if there's an upward path from x to y and one from y to z, then there's such a path from x to z. In fact, if you define a relation using a graph in this way, the relation will be transitive.)

However, this graph does not define a total order. Trichotomy fails for d and e, since $d < e$ , $e < d$ , and $d = e$ are all false.

Definition. Let S be a partially ordered set, and let T be a subset of S.

(a) $s \in S$ is an upper bound for T if $s \ge t$ for all $t \in T$ .

(b) $s \in S$ is a lower bound for T if $s \le t$ for all $t \in T$ .

Thus, an upper bound for a subset is an element which is greater than or equal to everything in the subset; a lower bound for a subset is an element which is less than or equal to everything in the subset. Note that unlike the largest element or smallest element of a subset, upper and lower bounds don't need to belong to the subset.

For instance, consider the subset $T = (0, 1]$ of $\real$ . 2 is an upper bound for T, since $2 \ge x$ for all $x \in T$ . 1 is also an upper bound for T. Note that 2 is not an element of T while 1 is an element of T. In fact, any real number greater than or equal to 1 is an upper bound for T.

Likewise, any real number less than or equal to 0 is a lower bound for T.

T has a largest element, namely 1. It does not have a smallest element; the obvious candidate 0 is not in T.

This example shows that a subset may have many --- even infinitely many --- upper or lower bounds. Among all the upper bounds for a set, there may be one which is smallest.

Definition. Let S be a partially ordered set, and let T be a subset of S. An element $s_0 \in S$ is a least upper bound for T if:

(a) $s_0$ is an upper bound for T.

(b) If s is an upper bound for T, then $s_0 \le s$ .

The idea is that $s_0$ is an upper bound by (a); it's the least upper bound, since (b) says $s_0$ is smaller than any other upper bound.

Definition. Let S be a partially ordered set, and let T be a subset of S. An element $s_0 \in S$ is a greatest lower bound for T if:

(a) $s_0$ is an lower bound for T.

(b) If s is an lower bound for T, then $s_0 \ge s$ .

The concepts of least upper bound and greatest lower bound come up often in analysis. I'll give a simple example.

Example. Determine the least upper bound and greatest lower bound for the following sets (if they exist):

(a) The subset $S = (0, 1]$ of $\real$ .

(b) The subset $T = (0, +\infty)$ of $\real$ . (Thus, T is the positive real axis, not including 0.)

(a) Any real number greater than or equal to 1 is an upper bound for T. Among the upper bounds for S, it's clear that 1 is the smallest, so 1 is the least upper bound for S.

Likewise, any real number less than or equal to 0 is a lower bound for S. But among the lower bounds for S, it's clear that 0 is the largest, so 0 is the greatest lower bound for S.

Notice that $1 \in S$ , but $0 \notin S$ . The least upper bound and greatest lower bound may be contained, or not contained, in the set.

(b) T has no least upper bound in $\real$ ; in fact, T has no upper bound in $\real$ .

0 is the greatest lower bound for T in $\real$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga