Set Algebra

Mathematicians tend to prove results about sets as they need them, rather than memorizing and using a large collection of rules. There are a lot of rules involving sets; you'll probably become familiar with the most important ones simply by using them a lot.

Usually you can check informally (for instance, by using a Venn diagram) whether a rule is correct; if necessary, you should be able to write a proof. In most cases, you can give a proof by going back to the definitions of set contructions in terms of elements.

Once you've compiled a collection of known facts about sets, you can use those facts to prove other facts.

There are also various styles for these proofs. You can write a proof formally, as a series of implications or double implications.

Alternatively, you can give a proof that relies more on words.

Example. ( Distributivity) Let A, B, and C be sets. Prove that

$A \cap (B \cup C) = (A \cap B) \cup (A \cap C).$

If X and Y are sets, if and only if for all x, $x \in X$ if and only if $x \in Y$ .

First, I'll give a formal proof, written as a series of double implications:

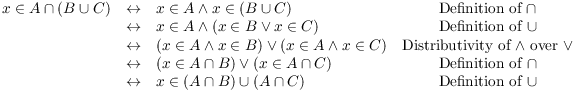
$\matrix{x \in A \cap (B \cup C) & \iff & x \in A \land x \in (B \cup C) \hfill & \hbox{Definition of $\cap$} \cr & \iff & x \in A \land (x \in B \lor x \in C) \hfill & \hbox{Definition of $\cup$} \cr & \iff & (x \in A \land x \in B) \lor (x \in A \land x \in C) \hfill & \hbox{Distributivity of $\land$ over $\lor$} \cr & \iff & (x \in A \cap B) \lor (x \in A \cap C) \hfill & \hbox{Definition of $\cap$} \cr & \iff & x \in (A \cap B) \cup (A \cap C) \hfill & \hbox{Definition of $\cup$} \cr}$

I've shown that

$x \in A \cap (B \cup C) \iff x \in (A \cap B) \cup (A \cap C).$

By definition of set equality, this proves that $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ .

The idea of the proof was to reduce everything to statements about elements. Then I used logical rules to manipulate the element statements.

Here's an alternative proof written with more words. I'll prove $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ by showing that each set is contained in the other.

First, I'll show that $A \cap (B \cup C) \subset (A \cap B) \cup (A \cap C)$ . Let $x \in A \cap (B \cup C)$ . By definition of intersection, this means that $x \in A$ and $x \in B \cup C$ .

Now $x \in B \cup C$ means, by definition of union, $x \in B$ or $x \in C$ . Combining this with the fact that $x \in A$ , this means that either $x \in A$ and $x \in B$ , or $x \in A$ and $x \in C$ .

By definition of intersection (twice), this means that either $x \in A \cap B$ or $x \in A \cap C$ . And by the definition of union, this means that $x \in (A \cap B) \cup (A \cap C)$ .

I've shown that if $x \in A \cap (B \cup C)$ , then $x \in (A \cap B) \cup (A \cap C)$ . By definition of subset, $A \cap (B \cup C) \subset (A \cap B) \cup (A \cap C)$ .

Next, I'll show that $(A \cap B) \cup (A \cap C) \subset A \cap (B \cup C)$ . Let $x \in (A \cap B) \cup (A \cap C)$ . By definition of union, $x \in A \cap B$ or $x \in A \cap C$ .

In the first case, $x \in A \cap B$ . By definition of intersection, this means $x \in A$ and $x \in B$ . Now by constructing a disjunction, $x \in B$ gives $x \in B$ or $x \in C$ , and by definition of union, I get $x \in B \cup C$ .

Since I know $x \in A$ , the definition of intersection gives $x \in A \cap (B \cup C)$ .

In the second case, $x \in A \cap C$ . By definition of intersection, this means $x \in A$ and $x \in C$ . Now by constructing a disjunction, $x \in C$ gives $x \in B$ or $x \in C$ , and by definition of union, I get $x \in B \cup C$ .

Since I know $x \in A$ , the definition of intersection gives $x \in A \cap (B \cup C)$ .

Since in both cases I have $x \in A \cap (B \cup C)$ , I have shown that if $x \in (A \cap B) \cup (A \cap C)$ , then $x \in A \cap (B \cup C)$ . By definition of subset, this means that $(A \cap B) \cup (A \cap C) \subset A \cap (B \cup C)$ .

Finally, since I've shown that $A \cap (B \cup C)$ and $(A \cap B) \cup (A \cap C)$ are each contained in the other, they must be equal: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ .

You can see that the first proof is shorter, but sometimes shorter proofs require more thinking to understand: The proof is shorter because the reasoning is compressed. The second proof is much longer, but maybe the words make more sense to you.

Note: It's also true that

$A \cup (B \cap C) = (A \cup B) \cap (A \cup C).$

Example. ( DeMorgan's Law) Let A and B be sets. Prove that

$\overline{A \cup B} = \overline{A} \cap \overline{B} \quad\hbox{and}\quad \overline{A \cap B} = \overline{A} \cup \overline{B}.$

I'll just prove the first statement; the second is similar. This proof will illustrate how you can work with complements. I'll use the logical version of DeMorgan's law to do the proof.

Let x be an arbitrary element of the universe.

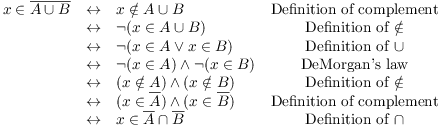
$\matrix{x \in \overline{A \cup B} & \iff & x \notin A \cup B \hfill & \hbox{Definition of complement} \cr & \iff & \lnot(x \in A \cup B) \hfill & \hbox{Definition of $\notin$} \cr & \iff & \lnot(x \in A \lor x \in B) \hfill & \hbox{Definition of $\cup$} \cr & \iff & \lnot(x \in A) \land \lnot(x \in B) \hfill & \hbox{DeMorgan's law} \cr & \iff & (x \notin A) \land (x \notin B) \hfill & \hbox{Definition of $\notin$} \cr & \iff & (x \in \overline{A}) \land (x \in \overline{B}) \hfill & \hbox{Definition of complement} \cr & \iff & x \in \overline{A} \cap \overline{B} \hfill & \hbox{Definition of $\cap$} \cr}$

Therefore, $\overline{A \cup B} = \overline{A} \cap \overline{B}$ .

Example. Let A and B be sets. Prove that $A \cap B \subset A$ .

This example will show how you prove a subset relationship.

By definition, if X and Y are sets, $X \subset Y$ if and only if for all x, if $x \in X$ , then $x \in Y$ .

Take an arbitrary element x. Suppose $x \in A \cap B$ (conditional proof). I want to show that $x \in A$ .

$x \in A \cap B$ means that $x \in A$ and $x \in B$ , by definition of intersection. But $x \in A$ and $x \in B$ implies $x \in A$ (decomposing a conjunction), and this is what I wanted to show. Therefore, $A \cap B \subset A$ .

By the way, you usually don't write the logic out in such gory detail. The proof above could be shortened to the following.

$x \in A \cap B$ means that $x \in A$ and $x \in B$ , so in particular $x \in A$ . Therefore, $A \cap B \subset A$ .

The "in particular" substitutes for decomposing the conjunction.

The procedure I've followed is so common that it's worth pointing it out: To prove a subset relationship (an inclusion) $X \subset Y$ , take an arbitrary element of X and prove that it must be in Y.

In the next example, I'll need the following facts from logic. First, $P \lor \lnot P$ is a tautology:

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & $\lnot P$ & & $P \lor \lnot P$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

Also, $P \land (\hbox{a tautology}) \iff P$ :

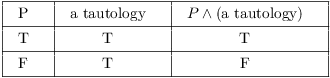
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & a tautology & & $P \land (\hbox{a tautology})$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

In effect, this means that I can drop tautologies from "and" statements. I'll just call this "Dropping tautologies" in the proof below.

Example. Prove that $(A - B) \cup (B - A) = (A \cup B) - (A \cap B)$ .

$\matrix{x \in (A - B) \cup (B - A) \iff & \cr x \in (A - B) \lor x \in (B - A) \iff & \hbox{Definition of union} \cr (x \in A \land x \notin B) \lor (x \in B \land x \notin A) \iff & \hbox{Definition of complement} \cr [x \in A \lor (x \in B \land x \notin A)] \land [x \notin B \lor (x \in B \land x \notin A)] \iff & \hbox{Distributivity} \cr (x \in A \lor x \in B) \land (x \in A \lor x \notin A)] \land (x \notin B \lor x \in B) \land (x \notin B \lor x \notin A) \iff & \hbox{Distributivity} \cr (x \in A \lor x \in B) \land (x \notin B \lor x \notin A) \iff & \hbox{Dropping tautologies} \cr (x \in A \lor x \in B) \land (\lnot x \in B \lor \lnot x \in A) \iff & \hbox{Definition of ``not in''} \cr (x \in A \lor x \in B) \land \lnot (x \in B \land x \in A) \iff & \hbox{DeMorgan} \cr (x \in A \cup B) \land \lnot (x \in A \cap B) \iff & \hbox{Definition of union and} \cr & \hbox{intersection} \cr x \in (A \cup B) - (A \cap B) & \hbox{Definition of complement} \cr}$

Therefore, $(A - B) \cup (B - A) = (A \cup B) - (A \cap B)$ .

Example. Let A be a set. Prove that

$A \cup \emptyset = A \quad\hbox{and}\quad A \cap \emptyset = \emptyset.$

This example will show how you can deal with the empty set.

To prove $A \cup \emptyset = A$ , let x be an arbitrary element of the universe. First, by definition of $\cup$ ,

$x \in A \cup \emptyset \iff (x \in A) \lor (x \in \emptyset).$

I'll show that $[(x \in A) \lor (x \in \emptyset)] \iff (x \in A)$ . To prove $P \iff Q$ , I must prove $P \ifthen Q$ and $Q \ifthen P$ .

First, if $x \in A$ , then $(x \in A) \lor (x \in \emptyset)$ (constructing a disjunction).

Next, suppose $(x \in A) \lor (x \in \emptyset)$ . The second statement $x \in \emptyset$ is false for all x, by definition of $\emptyset$ . But the $\lor$ -statement is true by assumption, so $x \in A$ must be true by disjunctive syllogism. This proves that if $(x \in A) \lor (x \in \emptyset)$ , then $x \in A$ .

This completes my proof that $[(x \in A) \lor (x \in \emptyset)] \iff (x \in A)$ . So

$\matrix{ x \in A \cup \emptyset & \iff & (x \in A) \lor (x \in \emptyset) \hfill & \hbox{Definition of $\cup$} \cr & \iff & x \in A \hfill & \hbox{Proved above} \cr}$

Therefore, $A \cup \emptyset = A$ .

To prove that $A \cap \emptyset = \emptyset$ , I must prove that for all x, $x \in A \cap \emptyset$ if and only if $x \in \emptyset$ .

As usual, x be an arbitrary element of the universe. To prove $x \in A \cap \emptyset$ if and only if $x \in \emptyset$ , I must prove that the following implications:

$(x \in A \cap \emptyset) \ifthen x \in \emptyset \quad\hbox{and}\quad x \in \emptyset \ifthen (x \in A \cap \emptyset)$

I'll do this by showing that, in each case, the antecedent (i.e. the "if" part of the statement) is false --- since by basic logic, if P is false, then $P \ifthen Q$ is true.

For the first implication, consider the statement $x \in A \cap \emptyset$ . By definition of intersection,

$x \in A \cap \emptyset \iff (x \in A \land x \in \emptyset).$

Now $x \in \emptyset$ is false, by definition of the empty set. Therefore, the conjunction $x \in A \land x \in \emptyset$ is also false. Hence, $x \in A \cap \emptyset$ is false.

It follows that the implication $x \in A \cap \emptyset \ifthen x \in \emptyset$ is true, because the "if" part is false.

Likewise, the second implication $x \in \emptyset \ifthen (x \in A \cap \emptyset)$ is true because $x \in \emptyset$ is false, by definition of the empty set.

Since both implications are true, $x \in A \cap \emptyset$ if and only if $x \in \emptyset$ . And this in turn proves that $A \cap \emptyset = \emptyset$ .

Contact information

Bruce Ikenaga's Home Page