Sets

Roughly speaking, a set is a collection of objects. The objects are called the members or the elements of the set.

Set theory is the basis for mathematics, and there are a number of axiom systems for set theory; von Neumann-G\"odel-Bernays (NBG) and Zermelo-Fraenkel-Choice (ZFC) are the most well-known. I'll give an informal exposition here, without referring to an axiom system.

You construct or define a set by saying what its elements are.

You can define a set by listing its elements between curly brackets:

$\{1, 2, 3, \hbox{Calvin}\}.$

I've been using the "element of" notation for a while.

Definition. $x \in S$ means that x is an element of the set X.

$x \notin S$ means that x is not an element of S.

The order of the elements in the list of elements of a set is irrelevant. Thus,

$\{1, 2, 3, \hbox{Calvin}\} \quad\hbox{is the same as}\quad \{\hbox{Calvin}, 2, 1, 3\}.$

Definition. Let X and Y be sets. Then if and only if X and Y have the same elements.

It's understood when you list the elements of a set that no duplicates are allowed: You don't write things like " $\{1, 2, 3, 3\}$ ".

You can also define a set using set constructor notation. Here's an example:

$\{n \in \integer \mid n = m^2 \quad\hbox{for}\quad m \in \integer\}.$

The set constructor consists of two statements separated by a " $\mid$ ", contained in curly brackets. The two statements together give the properties which must be satisfied by an element of the set. (Thus, the " $\mid$ " functions like a logical "and".)

Some people prefer to follow the rule used above: The statement to the left of the " $\mid$ " says what big set the constructed set is a subset of, while the statement to the right of the " $\mid$ " gives the membership criteria for the subset.

However, it is common to write the preceding set as

$\{m^2 \mid m \in \integer\}.$

This is simpler to write, and avoids the introduction of the unnecssary variable n in the first definition. I'll usually use the second version wherever possible.

This set consists of all integers which are perfect squares. I could write this more explicitly (but less precisely) as

$\{0, 1, 4, 9, \ldots\}.$

This is less precise because the "..." assumes that it is clear what the pattern is. However, seeing a number of "sample" elements can make it more obvious what members of the set look like. There's no harm in doing this as long as there's no chance of confusion.

Here's an example using two variables:

$\{(x, y) \mid x, y \in \real \quad\hbox{and}\quad y = x^2\}.$

I could also write this as

$\{(x, x^2) \mid x \in \real\}.$

This set consists of pairs of real numbers such that the second is the square of the first. (By the way, the last sentence gives a verbal description of the set. It's useful to say things in words when the symbols get confusing.) Here are some elements of the set:

$(-1,1), (0,0), (\sqrt{3}, 3), (1.1, 1.21), \ldots.$

The set in question is actually the graph of .

In this case, I can't list the elements of the set --- when I discuss cardinality, I'll explain why --- and thus, it's particularly important to have a set constructor definition available.

You can also have sets whose elements are sets. For example:

$\{\{1, 2\}, \{3, \hbox{Calvin}\}, \pi\}.$

This is a set with three elements, two of which are sets with two elements.

Definition. Let X be a set. The cardinality of X is denoted . For a finite set, it is the number of elements in X.

We'll leave aside for the moment what cardinality means for infinite sets. However, I'll note that there are different kinds of "infinite"!

Thus,

$|\{1, 4, -19\}| = 3, \quad\hbox{and}\quad |\{0\}| = 1.$

Definition. The set with no elements is called the empty set, and is denoted $\emptyset$ or $\{\hphantom{\cdot}\}$ .

Note that $|\emptyset| = 0$ : The empty set is the only set with zero elements.

Remark. You have to be careful in constructing sets in order to avoid set-theoretic paradoxes. For example, here is Russell's paradox. Consider "the set S of all sets which are not members of themselves". Is S an element of S?

If S is an element of S, then by definition S is not a member of itself --- contradicting my assumption that S is an element of S.

If S is not an element of S, then S is an element of S, since S consists of sets which are not members of themselves. This is also a contradiction.

By the Law of the Excluded Middle, either S is an element of S, or it is not --- but both alternatives lead to contradictions.

Paradoxes of this kind are avoided by setting up axioms for set theory which do not allow the construction of sets such as this one.

We've been using some standard notations for certain sets that occur often in mathematics. Here's a recap:

$\integer$ is the set of integers.

$\rational$ is the set of rational numbers.

$\real$ is the set of real numbers.

$\complex$ is the set of complex numbers.

If you just want the positive integers (also known as the natural numbers, use $\integer^+$ or $\natural$ ; if you want the nonnegative integers (sometimes called the whole numbers), use $\integer^{\ge 0}$ . Note that some people include 0 in $\natural$ (so by the "natural numbers" they mean $\integer^{\ge 0}$ ). To avoid confusion, it's probably better to refer to the "positive integers" or "nonnegative integers".

Definition. Let S and T be sets. T is a subset of S if and only if $x \in T$ implies $x \in S$ . $T \subset S$ means that T is a subset of S, and $T \not\subset S$ means that T is not a subset of S.

This picture illustrates $T \subset S$ :

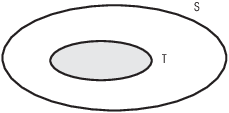
$\hbox{\epsfysize=1in \epsffile{sets1.eps}}$

The picture above is called a Venn diagram. Venn diagrams are often useful for picturing sets and relationships among sets. Be careful not to substitute diagrams for proofs, however!

Remarks. (a) Some people use " $T \subset S$ " to mean that T is a subset of S, but is not equal to S. A subset of S other than S itself is called a proper subset of S. With this convention, you write $T \subseteq S$ to mean that T is a subset of S, possibly S itself.

I prefer to write $T \subset S$ to mean T is any subset of S. If I want T to be a proper subset of S, I'll write $T \propersubset S$ . Reason: More often than not, you want to include the possibility that , and you should use the simpler notation ( $\subset$ rather than $\subseteq$ ) for the case that occurs more often.

On the other hand, some people prefer $T \subseteq S$ because it is analogous to writing $x \le y$ when x and y are numbers.

(b) if and only if $S \subset T$ and $T \subset S$ .

To see this, note that the relations $S \subset T$ and $T \subset S$ means that every element of S is an element of T, and every element of T is an element of S --- that is, S and T have the same elements.

We'll often prove that two sets are equal by showing that each is a subset of the other.

(c) If (that is, X is a set with n elements) and S is a subset of X, then each element of X can either be an element of S or not. Thus, there are 2 choices for each element. It follows that X has subsets. (Remember that this includes both the empty set and X itself.)

Example. List the subsets of:

(a) $\{a, f, g\}$ .

(b) $\{a, \{f, g\}\}$ .

(a) The set has 3 elements, so it has subsets:

$\{\emptyset, \{a\}, \{f\}, \{g\}, \{a, f\}, \{a, g\}, \{f, g\}, \{a, f, g\}\}.$

Notice that you must write " $\{a\}$ ", not "a". It is the set with the single element a, whereas a by itself is not a set.

(b) The set has 2 elements, namely a and $\{f, g\}$ . Notice that you don't "unpack" $\{f, g\}$ .

Think of a set as a bag. The set $\{a, \{f, g\}\}$ contains a single element a and another bag (which happens to contain two elements f and g). The number of things in $\{a, \{f, g\}\}$ "at the outer level" is 2.

It follows that the set has subsets:

$\{\emptyset, \{a\}, \{\{f, g\}\}, \{a, \{f, g\}\}\}.$

Notice that " $\{\{f, g\}\}$ " got "double-bagged: It is a set containing a set.

Example. Let

$A = \{n \in \integer \mid n = 2m \quad\hbox{for some}\quad m \in \integer\} \quad\hbox{and}\quad B = \{n \in \integer \mid n = 6m \quad\hbox{for some}\quad m \in \integer\}.$

Prove that $B \subset A$ .

To prove that $B \subset A$ , I must show that if $n \in B$ , then $n \in A$ . You can often prove set inclusion or equality by considering elements.

Let $n \in B$ . By definition of B, I have for some $m \in \integer$ . Now

Since m is an integer, so is . Therefore, n has the form $2 \cdot (\hbox{an integer})$ , so by definition $n \in A$ .

Hence, $B \subset A$ .

Lemma. Let S and T be sets.

(a) $\emptyset \subset S$ .

(b) $S \subset S$ .

Proof. (a) To prove that $\emptyset \subset S$ , I have to prove that if $x \in \emptyset$ , then $x \in S$ . But $x \in \emptyset$ is false for all x, so the conditional statement must be true. (In this situation, you often say that the statement is vacuously true --- the condition is satisfied because there are no cases!)

(b) To prove that $S \subset S$ , I must show that if $x \in S$ , then $x \in S$ . This is trivially true --- $P \ifthen P$ is a tautology --- so $S \subset S$ .

When one is discussing sets, there is usually a "big set" which contains all the sets under discussion. This "big set" is usually called the universe; usually, it will be clear from the context what it is. For example, if I'm discussing sets of integers, the universe is the set of integers $\integer$ . If I'm discussing sets of real numbers, the universe is the set of real numbers $\real$ .

Definition. (a) Let S and T be sets in the universe X. The complement of S is the set of elements of the universe which are not contained in S; it is denoted $\overline{S}$ or . Thus,

$\overline{S} = \{x \in X \mid x \notin S\}.$

(b) The (relative) complement of S in T is the set of elements of T which are not elements of S; it is denoted . Thus,

$T - S = \{x \in T \mid x \notin S\}.$

Here's a picture; the shaded area is .

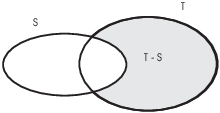
$\hbox{\epsfysize=1in \epsffile{sets2.eps}}$

Set complements function likes logical negations; the analogy even extends to DeMorgan's Laws, as I'll show below.

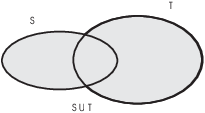
Definition. Let S and T be sets. The union of S and T is the set whose elements are elements of S or elements of T; it is denoted $S \cup T$ . That is,

$S \cup T = \{x \mid x \in S \quad\hbox{or}\quad x \in T\}.$

Picture:

$\hbox{\epsfysize=1in \epsffile{sets3.eps}}$

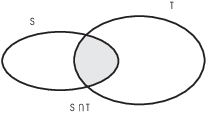
Definition. Let S and T be sets. The intersection of S and T is the set whose elements are elements of both S and T; it is denoted $S \cap T$ . That is,

$S \cap T = \{x \mid x \in S \quad\hbox{and}\quad x \in T\}.$

Picture:

$\hbox{\epsfysize=1in \epsffile{sets4.eps}}$

Note that the "or" and "and" in the last two definitions are the logical "or" and "and".

Example. Suppose the universe is the set of positive integers:

$X = \{1, 2, 3, 4, \ldots \}.$

Suppose

$A = \{1, 2, 3, 4, 6, 8\} \quad\hbox{and}\quad B = \{4, 6, 8, 10, 12\}.$

Find the elements of the following sets:

(a) $\overline{A}$ .

(b) .

(d) $A \cup B$ .

(e) $A \cap B$ .

(a) $\overline{A} = \{5, 7, 9, 10, 11, 12, 13, \ldots\}$ . That is, the set consisting of 5, 7, and all integers greater than or equal to 9.

(b) $A - B = \{1, 2, 3\}$ .

(d) $A \cup B = \{1, 2, 3, 4, 6, 8, 10, 12\}$ .

(e) $A \cap B = \{4, 6, 8\}$ .

You've probably seen interval notation in other courses (for example, in writing solutions to inequalities). Suppose a and b are real numbers, where $a \le b$ .

$(a, b) = \{x \in \real \mid a < x < b\}$

$[a, b] = \{x \in \real \mid a \le x \le b\}$

$[a, b) = \{x \in \real \mid a \le x < b\}$

$(a, b] = \{x \in \real \mid a < x \le b\}$

We also have half-infinite intervals:

$(a, \infty) = \{x \in \real \mid x > a\}$

$[a, \infty) = \{x \in \real \mid x \ge a\}$

$(-\infty, a) = \{x \in \real \mid x < a\}$

$(-\infty, a] = \{x \in \real \mid x \le a\}$

In some cases, we'll need to "take apart" a compound inequality like " " in order to do a proof. A compound inequality is a conjunction (an "and") of two inequalities:

$a < x < b \quad\hbox{means}\quad (a < x) \land (x < b)$

Similar remarks hold when " " is replaced with " $\le$ ".

Before I get to the following examples, here's are suggestions for reading these kinds of proofs. The very best thing might be to take the problem statement in the example and see if you can write a proof by yourself --- maybe peeking at the solution when you get stuck.

If you want to simply read these solutions through, check each statement, writing out additional notes or details yourself if something isn't clear. You have to work --- reading a proof is not like reading a comic book! As you read proofs that are longer and more difficult, you should expect to have to work harder --- doing math is like doing exercise. You may not be able to grasp the big picture of a proof the first time through, but at least try to understand the individual steps.

Example. Prove that $(1, 4) \cap [3, 10] = [3, 4)$ .

To show two sets are equal, you can show each is contained in the other.

It's possible to write this proof out using lots of logical notation, but I think it makes it somewhat forbidding to read. Hence, I'll write the proof using a combination of symbols and words.

First, I'll prove that $(1, 4) \cap [3, 10] \subset [3, 4)$ .

Let $x \in (1, 4) \cap [3, 10]$ . By the definition of intersection, this means that $x \in (1, 4)$ and $x \in [3, 10]$ . These statements are equivalent to the compound inequalities

$1 < x < 4 \quad\hbox{and}\quad 3 \le x \le 10.$

As I noted above, each of these compound inequalities can be broken down into two simple inequalities. Doing so, I get

$1 < x \quad\hbox{and}\quad x < 4 \quad\hbox{and}\quad 3 \le x \quad\hbox{and}\quad x \le 10.$

In particular, I have $3 \le x$ and . These simple inequalities are the same as $3 \le x < 4$ . But this implies that $x \in [3, 4)$ .

I've shown that if $x \in (1, 4) \cap [3, 10]$ , then $x \in [3, 4)$ . This proves that $(1, 4) \cap [3, 10] \subset [3, 4)$ .

Next, I'll show that $[3, 4) \subset (1, 4) \cap [3, 10]$ .

Let $x \in [3, 4)$ . This means that $3 \le x < 4$ , or

$3 \le x \quad\hbox{and}\quad x < 4.$

First, , so together with $3 \le x$ I get .

Next, , so together with I get . Hence, $x \le 10$ .

(It's interesting to see how the last "Hence" follows from our rules of logic. By the rule for constructing a disjunction, " " gives " or ". But " or " is the same as " $x \le 10$ ". You may not have realized before that " $\le$ " contains a logical "or"!)

Continuing with my proof, I have and , so . Therefore, $x \in (1, 4)$ .

Likewise, I have $3 \le x$ and $x \le 10$ , so $3 \le x \le 10$ . Therefore, $x \in [3, 10]$ .

Since $x \in (1, 4)$ and $x \in [3, 10]$ , I have $x \in (1, 4) \cap [3, 10]$ by definition of intersection. This proves that $[3, 4) \subset (1, 4) \cap [3, 10]$ .

Finally, since $(1, 4) \cap [3, 10] \subset [3, 4)$ and $[3, 4) \subset (1, 4) \cap [3, 10]$ , I've proven that $(1, 4) \cap [3, 10] = [3, 4)$ .

Example. Prove that $[-3, 6] \cup [1, 8] = [-3, 8]$ .

I will show that each of the sets $[-3, 6] \cup [1, 8]$ and is contained in the other.

Suppose $x \in [-3, 6] \cup [1, 8]$ . By definition of union, $x \in [-3, 6]$ or $x \in [1, 8]$ . There are two cases.

If $x \in [-3, 6]$ , then $-3 \le x \le 6$ . But $6 \le 8$ , so $-3 \le x \le 8$ . Hence, $x \in [-3, 8]$ .

If $x \in [1, 8]$ , then $1 \le x \le 8$ . But $-3 \le 1$ , so $-3 \le x \le 8$ . Hence, $x \in [-3, 8]$ .

Thus, $x \in [-3, 8]$ holds in both cases. This shows that $[-3, 6] \cup [1, 8] \subset [-3, 8]$ .

Now suppose $x \in [-3, 8]$ . Then $-3 \le x \le 8$ .

The idea is that the four numbers which make up the endpoints of the intervals are arranged this way:

$\matrix{ -3 & & 6 & \cr & 1 & & 8 \cr}$

I will take two cases by picking a number between 1 and 6. I choose 3.

Now $-3 \le x \le 8$ , so either $-3 \le x \le 3$ or $3 < x \le 8$ . Consider the two cases.

First, suppose $-3 \le x \le 3$ . But $3 \le 6$ , so $-3 \le x \le 6$ . Therefore, $x \in [-3, 6]$ . Hence, $x \in [-3, 6] \cup [1, 8]$ .

(If you think about it, this is constructing a disjunction: $x \in [-3, 6]$ gives $x \in [-3, 6]$ or $x \in [1, 8]$ , which in turn implies $x \in [-3, 6] \cup [1, 8]$ .)

Second, suppose $3 < x \le 8$ . But $1 \le 3$ , so $1 \le x \le 8$ . Therefore, $x \in [1, 8]$ . Hence, $x \in [-3, 6] \cup [1, 8]$ .

Thus, $x \in [-3, 6] \cup [1, 8]$ holds in both cases. This shows $[-3, 8] \subset [-3, 6] \cup [1, 8]$ .

This completes the proof that $[-3, 6] \cup [1, 8] = [-3, 8]$ .

Example. Let

$\real^{\ge 0} = \{x \in \real \mid x \ge 0\} \quad\hbox{and}\quad \real^{\le 0} = \{x \in \real \mid x \le 0\}.$

Prove that $\real^{\ge 0} \cap \real^{\le 0} = \{0\}$ .

I'll prove the result by showing that $\{0\} \subset \real^{\ge 0} \cap \real^{\le 0}$ and that $\real^{\ge 0} \cap \real^{\le 0} \subset \{0\}$ .

To prove that $\{0\} \subset \real^{\ge 0} \cap \real^{\le 0}$ , I begin by taking an element of $\{0\}$ --- but the only element of $\{0\}$ is 0. So I have to show that $0 \in \real^{\ge 0} \cap \real^{\le 0}$ .

First, $0 \in \real^{\ge 0}$ because $0 \ge 0$ . Next, $0 \in \real^{\le 0}$ because $0 \le 0$ . Since $0 \in \real^{\ge 0}$ and $0 \in \real^{\le 0}$ , it follows that $0 \in \real^{\ge 0} \cap \real^{\le 0}$ . Hence, $\{0\} \subset \real^{\ge 0} \cap \real^{\le 0}$ .

Now I have to show that $\real^{\ge 0} \cap \real^{\le 0} \subset \{0\}$ . Let $x \in \real^{\ge 0} \cap \real^{\le 0}$ . By definition of intersection, this means that $x \in \real^{\ge 0}$ and $x \in \real^{\le 0}$ .

Since $x \in \real^{\ge 0}$ , I have $x \ge 0$ . Since $x \in \real^{\le 0}$ , I have $x \le 0$ . This means that , so $x \in \{0\}$ . Therefore, $\real^{\ge 0} \cap \real^{\le 0} \subset \{0\}$ .

This proves that $\real^{\ge 0} \cap \real^{\le 0} = \{0\}$ .

We'll see in doing set algebra proofs that Venn diagrams useful in checking that a set relationship is true. However, they become too complicated once there are more than 3 sets.

This is the general Venn diagram for three sets:

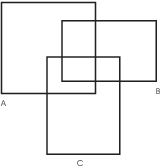
$\hbox{\epsfysize=1.5in \epsffile{sets5.eps}}$

Here are the Venn diagrams for some set constructed using complements, unions, and intersection:

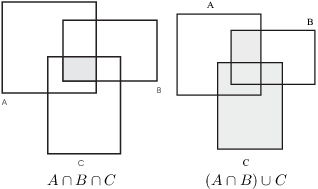
$\matrix{\hbox{\epsfysize=1.5in \epsffile{sets6.eps}} & \hbox{\epsfysize=1.5in \epsffile{sets7.eps}} \cr A \cap B \cap C & (A \cap B) \cup C \cr}$

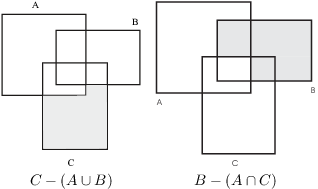
$\matrix{\hbox{\epsfysize=1.5in \epsffile{sets8.eps}} & \hbox{\epsfysize=1.5in \epsffile{sets9.eps}} \cr C - (A \cup B) & B - (A \cap C) \cr}$

Try to construct a general Venn diagram for 4 or 5 sets!

Contact information

Bruce Ikenaga's Home Page