Truth Tables, Tautologies, and Logical Equivalences

Mathematicians normally use a two-valued logic: Every statement is either True or False. This is called the Law of the Excluded Middle.

A statement in sentential logic is built from simple statements using the logical connectives $\lnot$ , $\land$ , $\lor$ , $\ifthen$ , and $\iff$ . The truth or falsity of a statement built with these connective depends on the truth or falsity of its components.

For example, the compound statement $P \ifthen (Q \lor \lnot R)$ is built using the logical connectives $\ifthen$ , $\lor$ , and $\lnot$ . The truth or falsity of $P \ifthen (Q \lor \lnot R)$ depends on the truth or falsity of P, Q, and R.

A truth table shows how the truth or falsity of a compound statement depends on the truth or falsity of the simple statements from which it's constructed. So we'll start by looking at truth tables for the five logical connectives.

Here's the table for negation:

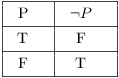
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & P & & $\lnot P$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & T & & F & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & F & & T & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

This table is easy to understand. If P is true, its negation $\lnot P$ is false. If P is false, then $\lnot P$ is true.

$P \land Q$ should be true when both P and Q are true, and false otherwise:

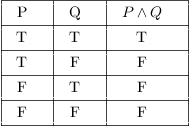
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & $P \land Q$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

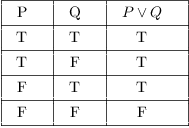
$P \lor Q$ is true if either P is true or Q is true (or both --- remember that we're using "or" in the inclusive sense). It's only false if both P and Q are false.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & $P \lor Q$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's the table for logical implication:

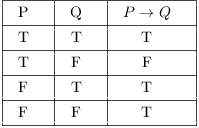
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & $P \ifthen Q$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

To understand why this table is the way it is, consider the following example:

"If you get an A, then I'll give you a dollar."

The statement will be true if I keep my promise and false if I don't.

Suppose it's true that you get an A and it's true that I give you a dollar. Since I kept my promise, the implication is true. This corresponds to the first line in the table.

Suppose it's true that you get an A but it's false that I give you a dollar. Since I didn't keep my promise, the implication is false. This corresponds to the second line in the table.

What if it's false that you get an A? Whether or not I give you a dollar, I haven't broken my promise. Thus, the implication can't be false, so (since this is a two-valued logic) it must be true. This explains the last two lines of the table.

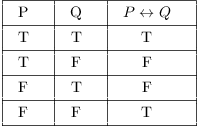
$P \iff Q$ means that P and Q are equivalent. So the double implication is true if P and Q are both true or if P and Q are both false; otherwise, the double implication is false.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & $P \iff Q$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

You should remember --- or be able to construct --- the truth tables for the logical connectives. You'll use these tables to construct tables for more complicated sentences. It's easier to demonstrate what to do than to describe it in words, so you'll see the procedure worked out in the examples.

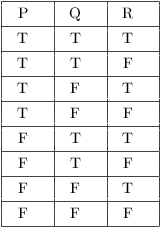
Remark. (a) When you're constructing a truth table, you have to consider all possible assignments of True (T) and False (F) to the component statements. For example, suppose the component statements are P, Q, and R. Each of these statements can be either true or false, so there are $2^3 = 8$ possibilities.

When you're listing the possibilities, you should assign truth values to the component statements in a systematic way to avoid duplication or omission. The easiest approach is to use lexicographic ordering. Thus, for a compound statement with three components P, Q, and R, I would list the possibilities this way:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & P & & Q & & R & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & T & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & T & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & F & & F & & F & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(b) There are different ways of setting up truth tables. You can, for instance, write the truth values "under" the logical connectives of the compound statement, gradually building up to the column for the "primary" connective.

I'll write things out the long way, by constructing columns for each "piece" of the compound statement and gradually building up to the compound statement. Any style is fine as long as you show enough work to justify your results.

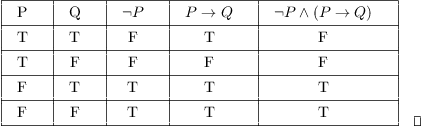
Example. Construct a truth table for the formula $\lnot P \land (P \ifthen Q)$ .

First, I list all the alternatives for P and Q.

Next, in the third column, I list the values of $\lnot P$ based on the values of P. I use the truth table for negation: When P is true $\lnot P$ is false, and when P is false, $\lnot P$ is true.

In the fourth column, I list the values for $P \ifthen Q$ . Check for yourself that it is only false ("F") if P is true ("T") and Q is false ("F").

The fifth column gives the values for my compound expression $\lnot P \land (P \ifthen Q)$ . It is an "and" of $\lnot P$ (the third column) and $P \ifthen Q$ (the fourth column). An "and" is true only if both parts of the "and" are true; otherwise, it is false. So I look at the third and fourth columns; if both are true ("T"), I put T in the fifth column, otherwise I put F.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & P & & Q & & $\lnot P$ & & $P \ifthen Q$ & & $\lnot P \land (P \ifthen Q)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & T & & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & F & & F & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & F & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

A tautology is a formula which is "always true" --- that is, it is true for every assignment of truth values to its simple components. You can think of a tautology as a rule of logic.

The opposite of a tautology is a contradiction, a formula which is "always false". In other words, a contradiction is false for every assignment of truth values to its simple components.

Example. Show that $(P \ifthen Q) \lor (Q \ifthen P)$ is a tautology.

I construct the truth table for $(P \ifthen Q) \lor (Q \ifthen P)$ and show that the formula is always true.

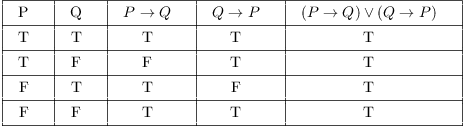
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & P & & Q & & $P \ifthen Q$ & & $Q \ifthen P$ & & $(P \ifthen Q) \lor (Q \ifthen P)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & F & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & T & & T & & F & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & F & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The last column contains only T's. Therefore, the formula is a tautology.

Example. Construct a truth table for $(P \ifthen Q) \land (Q \ifthen R)$ .

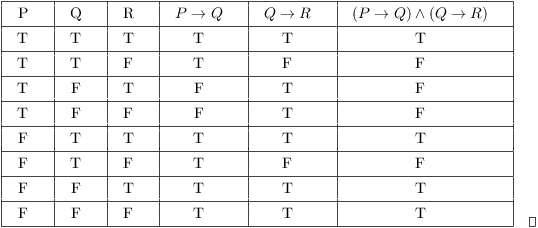
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & P & & Q & & R & & $P \ifthen Q$ & & $Q \ifthen R$ & & $(P \ifthen Q) \land (Q \ifthen R)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & T & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & T & & F & & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & T & & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & F & & F & & T & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & T & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & T & & F & & T & & F & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & F & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & F & & F & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

You can see that constructing truth tables for statements with lots of connectives or lots of simple statements is pretty tedious and error-prone. While there might be some applications of this (e.g. to digital circuits), at some point the best thing would be to write a program to construct truth tables (and this has surely been done).

The point here is to understand how the truth value of a complex statement depends on the truth values of its simple statements and its logical connectives. In most work, mathematicians don't normally use statements which are very complicated from a logical point of view.

Example. (a) Suppose that P is false and $P \lor \lnot Q$ is true. Tell whether Q is true, false, or its truth value can't be determined.

(b) Suppose that $(P \land \lnot Q) \ifthen R$ is false. Tell whether Q is true, false, or its truth value can't be determined.

(a) Since $P \lor \lnot Q$ is true, either P is true or $\lnot Q$ is true. Since P is false, $\lnot Q$ must be true. Hence, Q must be false.

(b) An if-then statement is false when the "if" part is true and the "then" part is false. Since $(P \land \lnot Q) \ifthen R$ is false, $P \land \lnot Q$ is true. An "and" statement is true only when both parts are true. In particular, $\lnot Q$ must be true, so Q is false.

Example. Suppose

"$x > y$ " is true.

"$\displaystyle \int f(x)\,dx = g(x) + C$ " is false.

"Calvin Butterball has purple socks" is true.

Determine the truth value of the statement

$$(x > y \ifthen \int f(x)\,dx = g(x) + C) \ifthen\,\lnot (\hbox{Calvin Butterball has purple socks})$$

For simplicity, let

P = "$x > y$ ".

Q = "$\displaystyle \int f(x)\,dx = g(x) + C$ ".

R = "Calvin Butterball has purple socks".

I want to determine the truth value of $(P \ifthen Q) \ifthen\,\lnot R$ . Since I was given specific truth values for P, Q, and R, I set up a truth table with a single row using the given values for P, Q, and R:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & P & & Q & & R & & $P \ifthen Q$ & & $\lnot R$ & & $(P \ifthen Q) \ifthen\,\lnot R$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & T & & F & & F & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Therefore, the statement is true.

Example. Determine the truth value of the statement

$$(10 > 42) \ifthen \hbox{``Ichabod Xerxes eats chocolate cupcakes''}$$

The statement "$10 > 42$ " is false. You can't tell whether the statement "Ichabod Xerxes eats chocolate cupcakes" is true or false --- but it doesn't matter. If the "if" part of an "if-then" statement is false, then the "if-then" statement is true. (Check the truth table for $P \ifthen Q$ if you're not sure about this!) So the given statement must be true.

Two statements X and Y are logically equivalent if $X \iff Y$ is a tautology. Another way to say this is: For each assignment of truth values to the simple statements which make up X and Y, the statements X and Y have identical truth values.

From a practical point of view, you can replace a statement in a proof by any logically equivalent statement.

To test whether X and Y are logically equivalent, you could set up a truth table to test whether $X \iff Y$ is a tautology --- that is, whether $X \iff Y$ "has all T's in its column". However, it's easier to set up a table containing X and Y and then check whether the columns for X and for Y are the same.

Example. Show that $P \ifthen Q$ and $\lnot P \lor Q$ are logically equivalent.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & P & & Q & & $P \ifthen Q$ & & $\lnot P$ & & $\lnot P \lor Q$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & T & & T & & F & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & T & & F & & F & & F & & F & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & T & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & F & & F & & T & & T & & T & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Since the columns for $P \ifthen Q$ and $\lnot P \lor Q$ are identical, the two statements are logically equivalent. This tautology is called Conditional Disjunction. You can use this equivalence to replace a conditional by a disjunction.

There are an infinite number of tautologies and logical equivalences; I've listed a few below; a more extensive list is given at the end of this section.

$$\matrix{ \hbox{Double negation} & \lnot(\lnot P) \iff P \cr \hbox{DeMorgan's Law} & \lnot(P \lor Q) \iff (\lnot P \land \lnot Q) \cr \hbox{DeMorgan's Law} & \lnot(P \land Q) \iff (\lnot P \lor \lnot Q) \cr \hbox{Contrapositive} & (P \ifthen Q) \iff (\lnot Q \ifthen\,\lnot P) \cr \hbox{Modus ponens} & [P \land (P \ifthen Q)] \ifthen Q \cr \hbox{Modus tollens} & [\lnot Q \land (P \ifthen Q)] \ifthen\,\lnot P \cr}$$

When a tautology has the form of a biconditional, the two statements which make up the biconditional are logically equivalent. Hence, you can replace one side with the other without changing the logical meaning.

You will often need to negate a mathematical statement. To see how to do this, we'll begin by showing how to negate symbolic statements.

Example. Write down the negation of the following statements, simplifying so that only simple statements are negated.

(a) $(P \lor \lnot Q)$

(b) $(P \land Q) \ifthen R$

(a) I negate the given statement, then simplify using logical equivalences. I've given the names of the logical equivalences on the right so you can see which ones I used.

$$\matrix{\lnot(P \lor \lnot Q) & \iff & \lnot P \land \lnot\lnot Q & \hbox{DeMorgan's law} \cr & \iff & \lnot P \land Q & \hbox{Double negation} \cr}\quad\halmos$$

(b)

$$\matrix{\lnot[(P \land Q) \ifthen R] & \iff & \lnot[\lnot(P \land Q) \lor R] & \hbox{Conditional Disjunction} \cr & \iff & \lnot\lnot(P \land Q) \land \lnot R & \hbox{DeMorgan's law} \cr & \iff & (P \land Q) \land \lnot R & \hbox{Double negation} \cr}$$

I showed that $(A \ifthen B)$ and $(\lnot A \lor B)$ are logically equivalent in an earlier example.

In the following examples, we'll negate statements written in words. This is more typical of what you'll need to do in mathematics. The idea is to convert the word-statement to a symbolic statement, then use logical equivalences as we did in the last example.

Example. Use DeMorgan's Law to write the negation of the following statement, simplifying so that only simple statements are negated:

"Calvin is not home or Bonzo is at the movies."

Let C be the statement "Calvin is home" and let B be the statement "Bonzo is at the moves". The given statement is $\lnot C \lor B$ . I'm supposed to negate the statement, then simplify:

$$\matrix{\lnot(\lnot C \lor B) & \iff & \lnot\lnot C \land \lnot B & \hbox{DeMorgan's Law} \cr & \iff & C \land \lnot B & \hbox{Double negation} \cr}$$

The result is "Calvin is home and Bonzo is not at the movies".

Example. Use DeMorgan's Law to write the negation of the following statement, simplifying so that only simple statements are negated:

"If Phoebe buys a pizza, then Calvin buys popcorn."

Let P be the statement "Phoebe buys a pizza" and let C be the statement "Calvin buys popcorn". The given statement is $P \ifthen C$ . To simplify the negation, I'll use the Conditional Disjunction tautology which says

$$(P \ifthen Q) \iff (\lnot P \lor Q)$$

That is, I can replace $P \ifthen Q$ with $\lnot P \lor Q$ (or vice versa).

Here, then, is the negation and simplification:

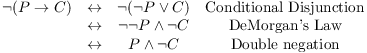
$$\matrix{\lnot(P \ifthen C) & \iff & \lnot(\lnot P \lor C) & \hbox{Conditional Disjunction} \cr & \iff & \lnot\lnot P \land \lnot C & \hbox{DeMorgan's Law} \cr & \iff & P \land \lnot C & \hbox{Double negation} \cr}$$

The result is "Phoebe buys the pizza and Calvin doesn't buy popcorn".

Next, we'll apply our work on truth tables and negating statements to problems involving constructing the converse, inverse, and contrapositive of an "if-then" statement.

Example. Replace the following statement with its contrapositive:

"If x and y are rational, then $x + y$ is rational."

By the contrapositive equivalence, this statement is the same as "If $x + y$ is not rational, then it is not the case that both x and y are rational".

This answer is correct as it stands, but we can express it in a slightly better way which removes some of the explicit negations. Most people find a positive statement easier to comprehend than a negative statement.

By definition, a real number is irrational if it is not rational. So I could replace the "if" part of the contrapositive with "$x + y$ is irrational".

The "then" part of the contrapositive is the negation of an "and" statement. You could restate it as "It's not the case that both x is rational and y is rational". (The word "both" ensures that the negation applies to the whole "and" statement, not just to "x is rational".)

By DeMorgan's Law, this is equivalent to: "x is not rational or y is not rational". Alternatively, I could say: "x is irrational or y is irrational".

Putting everything together, I could express the contrapositive as: "If $x + y$ is irrational, then either x is irrational or y is irrational".

(As usual, I added the word "either" to make it clear that the "then" part is the whole "or" statement.)

Example. Show that the inverse and the converse of a conditional are logically equivalent.

Let $P \ifthen Q$ be the conditional. The inverse is $\lnot P \ifthen\,\lnot Q$ . The converse is $Q \ifthen P$ .

I could show that the inverse and converse are equivalent by constructing a truth table for $(\lnot P \ifthen\,\lnot Q) \iff (Q \ifthen P)$ . I'll use some known tautologies instead.

Start with $\lnot P \ifthen\,\lnot Q$ :

$$\matrix{\lnot P \ifthen\,\lnot Q & \iff & \lnot\lnot Q \ifthen \lnot\lnot P & \hbox{Contrapositive} \cr & \iff & Q \ifthen P & \hbox{Double negation} \cr}$$

Remember that I can replace a statement with one that is logically equivalent. For example, in the last step I replaced $\lnot\lnot Q$ with Q, because the two statements are equivalent by Double negation.

Example. Suppose x is a real number. Consider the statement

"If $x^2 = 4$ , then $x = 2$ ."

Construct the converse, the inverse, and the contrapositive. Determine the truth or falsity of the four statements --- the original statement, the converse, the inverse, and the contrapositive --- using your knowledge of algebra.

The converse is "If $x = 2$ , then $x^2 = 4$ ".

The inverse is "If $x^2 \ne 4$ , then $x \ne 2$ ".

The contrapositive is "If $x \ne 2$ , then $x^2 \ne 4$ ".

The original statement is false: $(-2)^2 = 4$ , but $-2 \ne 2$ . Since the original statement is eqiuivalent to the contrapositive, the contrapositive must be false as well.

The converse is true. The inverse is logically equivalent to the converse, so the inverse is true as well.

\newpage

\centerline{\bigssbold List of Tautologies}

$$\matrix{ 1. \hfill & P \lor \lnot P \hfill & \hbox{Law of the excluded middle} \hfill \cr 2. \hfill & \lnot(P \land \lnot P) \hfill & \hbox{Contradiction} \hfill \cr 3. \hfill & [(P \ifthen Q) \land \lnot Q] \ifthen \lnot P \hfill & \hbox{ Modus tollens} \hfill \cr 4. \hfill & \lnot\lnot P \iff P \hfill & \hbox{Double negation} \hfill \cr 5. \hfill & [(P \ifthen Q) \land (Q \ifthen R)] \ifthen (P \ifthen R) \hfill & \hbox{Law of the syllogism} \hfill \cr 6. \hfill & (P \land Q) \ifthen P \hfill & \hbox{Decomposing a conjunction} \hfill \cr & (P \land Q) \ifthen Q \hfill & \hbox{Decomposing a conjunction} \hfill \cr 7. \hfill & P \ifthen (P \lor Q) \hfill & \hbox{Constructing a disjunction} \hfill \cr & Q \ifthen (P \lor Q) \hfill & \hbox{Constructing a disjunction} \hfill \cr 8. \hfill & (P \iff Q) \iff [(P \ifthen Q) \land (Q \ifthen P)] \hfill & \hbox{Definition of the biconditional} \hfill \cr 9. \hfill & (P \land Q) \iff (Q \land P) \hfill & \hbox{Commutative law for $\land$} \hfill \cr 10. \hfill & (P \lor Q) \iff (Q \lor P) \hfill & \hbox{Commutative law for $\lor$} \hfill \cr 11. \hfill & [(P \land Q) \land R] \iff [P \land (Q \land R)] \hfill & \hbox{Associative law for $\land$} \hfill \cr 12. \hfill & [(P \lor Q) \lor R] \iff [P \lor (Q \lor R)] \hfill & \hbox{Associative law for $\lor$} \hfill \cr 13. \hfill & \lnot(P \lor Q) \iff (\lnot P \land \lnot Q) \hfill & \hbox{DeMorgan's law} \hfill \cr 14. \hfill & \lnot(P \land Q) \iff (\lnot P \lor \lnot Q) \hfill & \hbox{DeMorgan's law} \hfill \cr 15. \hfill & [P \land (Q \lor R)] \iff [(P \land Q) \lor (P \land R)] \hfill & \hbox{Distributivity} \hfill \cr 16. \hfill & [P \lor (Q \land R)] \iff [(P \lor Q) \land (P \lor R)] \hfill & \hbox{Distributivity} \hfill \cr 17. \hfill & (P \ifthen Q) \iff (\lnot Q \ifthen \lnot P) \hfill & \hbox{Contrapositive} \hfill \cr 18. \hfill & (P \ifthen Q) \iff (\lnot P \lor Q) \hfill & \hbox{Conditional disjunction} \hfill \cr 19. \hfill & [(P \lor Q) \land \lnot P] \ifthen Q \hfill & \hbox{Disjunctive syllogism} \hfill \cr 20. \hfill & (P \lor P) \iff P \hfill & \hbox{Simplification} \hfill \cr 21. \hfill & (P \land P) \iff P \hfill & \hbox{Simplification} \hfill \cr}$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga