Approximation by Rational Numbers

Continued fractions give the best rational approximations to an irrational number. In this section, we'll see in what sense this is true.

The first lemma says that the denominators of convergents of continued fractions increase.

Lemma. Let , , , ... be a sequence of integers, where for $k \ge 1$ . Define

$p_0 = a_0, \quad q_0 = 1$

$p_1 = a_1 a_0 + 1, \quad q_1 = a_1$

$p_k = a_k p_{k-1} + p_{k-2}, \quad q_k = a_k q_{k-1} + q_{k-2} \quad\hbox{for}\quad k \ge 2.$

Then $q_{k+1} > q_k$ for .

Proof. Let . Note that $q_{k-1}$ is a positive integer, and $a_{k+1} \ge 1$ because the a's are positive integers from on. So

$q_{k+1} = a_{k+1} q_k + q_{k-1} > a_{k+1} q_k \ge 1\cdot q_k = q_k.\quad\halmos$

Theorem. Let x be irrational, and let $c_k = \dfrac{p_k}{q_k}$ be the k-th convergent in the continued fraction expansion of x. Suppose $p, q \in \integer$ , , and

Then $q \ge q_{k+1}$ .

Here's what the result means. Draw the line through the origin in the t-y plane with slope x. Plot the points and .

The hypothesis says that the vertical distance from to is less than the vertical distance from to .

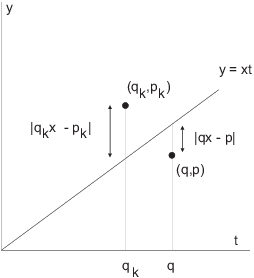
$\hbox{\epsfysize=2.5in \epsffile{approximation-by-rationals-1.eps}}$

The conclusion says that $q \ge q_{k+1}$ . In fact, since $q_{k+1} > q_k$ , I have : The denominator of $\dfrac{p}{q}$ is bigger than that of $\dfrac{p_k}{q_k}$ .

In other words, the only way the point can be closer to the line is if its y-coordinate is bigger.

Before beginning the proof, I'll note that it is a bit long and technical, though the individual steps aren't hard. I've tried to write out the details carefully, but if the informal discussion above gives you enough of an idea of what the theorem says, you could skip the proof and come back to it later if needed.

Proof. I'll give a proof by contradiction. Suppose that $q < q_{k + 1}$ .

Consider the equations

$\eqalign{ p_k u + p_{k + 1} v & = p \cr q_k u + q_{k + 1} v & = q \cr}$

u and v are defined as the solutions to these equations.

Think of this in matrix form:

$\left[\matrix{ p_k & p_{k + 1} \cr q_k & q_{k + 1} \cr}\right] \left[\matrix{u \cr v \cr}\right] = \left[\matrix{p \cr q \cr}\right].$

Using an earlier result on convergents, the determinant of the coefficient matrix is

$p_k q_{k + 1} - p_{k + 1} q_k = \pm 1.$

This means that when I solve the matrix equation by inverting the coefficient matrix, I get

$\left[\matrix{u \cr v \cr}\right] = \left[\matrix{ p_k & p_{k + 1} \cr q_k & q_{k + 1} \cr}\right]^{-1} \left[\matrix{p \cr q \cr}\right] = \pm \left[\matrix{ q_{k + 1} & -p_{k + 1} \cr -q_k & p_k \cr}\right] \left[\matrix{p \cr q \cr}\right] = \pm \left[\matrix{ q_{k + 1} p - p_{k + 1} q \cr -q_k p + p_k q \cr}\right].$

The point is that u and v are integers.

I'll now establish the contradiction in a series of steps.

Step 1. $u \ne 0$ and $v \ne 0$ .

Suppose . Then $p_k u + p_{k + 1} v = p$ gives $p_{k + 1} v = p$ , so

$p_{k + 1} q_{k + 1} v = p q_{k + 1}.$

Also, $q_k u + q_{k + 1} v = q$ gives $q_{k + 1} v = q$ , so

$p_{k + 1} q_{k + 1} v = q p_{k + 1}.$

That is,

$p q_{k + 1} = q p_{k + 1}.$

Thus, $q_{k + 1} \mid q p_{k + 1}$ . But $(p_{k + 1}, q_{k + 1}) = 1$ (as $p_{k + 1}$ and $q_{k + 1}$ are the numerator and the denominator of a convergent), so $q_{k + 1} \mid q$ . This is a contradiction, because I'm assuming that $q < q_{k + 1}$ . This proves that $u \ne 0$ .

Suppose . Then $p_k u + p_{k + 1} v = p$ gives . Also, $q_k u + q_{k + 1} v = q$ gives . Hence,

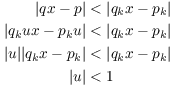
$\eqalign{ |q x - p| & < |q_k x - p_k| \cr |q_k u x - p_k u| & < |q_k x - p_k| \cr |u| |q_k x - p_k| & < |q_k x - p_k| \cr |u| & < 1 \cr}$

This implies , which contradicts $u \ne 0$ established above. Hence, $v \ne 0$ .

Step 2. u and v have opposite signs.

Since $v \ne 0$ , either or .

Suppose . Then $v \ge 1$ , so

$q_{k + 1} v \ge q_{k + 1} > q.$

Then $q_k u + q_{k + 1} v = q$ gives

$q_k u = q - q_{k + 1} v < 0.$

Since , I must have . Hence, u and v have opposite signs in this case.

Suppose . Then $q_{k + 1} v < 0$ , so $-q_{k + 1} v > 0$ . Therefore,

$q_k u = q - q_{k + 1} v = q + (-q_{k + 1} v) > 0.$

Since , I have . Hence, u and v have opposite signs in this case.

Step 3. and $q_{k + 1} x - p_{k + 1}$ have opposite signs.

The value x of the infinite continued fraction lies between any two consecutive convergents. Hence, either

$\dfrac{p_k}{q_k} < x < \dfrac{p_{k + 1}}{q_{k + 1}} \quad\hbox{or}\quad \dfrac{p_{k + 1}}{q_{k + 1}} < x < \dfrac{p_k}{q_k}.$

If $\dfrac{p_k}{q_k} < x < \dfrac{p_{k + 1}}{q_{k + 1}}$ , the first inequality gives , so . The second inequality gives $q_{k + 1} x < p_{k + 1}$ , so $q_{k + 1} x - p_{k + 1} < 0$ . Hence, and $q_{k + 1} x - p_{k + 1}$ have opposite signs in this case.

If $\dfrac{p_{k + 1}}{q_{k + 1}} < x < \dfrac{p_k}{q_k}$ , the first inequality gives $p_{k + 1} < q_{k + 1} x$ , so $q_{k + 1} x - p_{k + 1} > 0$ . The second inequality gives , so . Hence, and $q_{k + 1} x - p_{k + 1}$ have opposite signs in this case.

Step 4. and $v (q_{k + 1} x - p_{k + 1})$ have the same sign.

This follows from Steps 2 and 3 by checking the possible combinations of (opposite) signs:

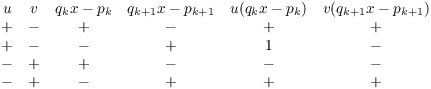
$\matrix{ u & v & q_k x - p_k & q_{k + 1} x - p_{k + 1} & u (q_k x - p_k) & v (q_{k + 1} x - p_{k + 1}) \cr + & - & + & - & + & + \cr + & - & - & + & 1 & - \cr - & + & + & - & - & - \cr - & + & - & + & + & + \cr}$

Step 5. (Final contradiction) Since and $v (q_{k + 1} x - p_{k + 1})$ have the same sign,

$|u (q_k x - p_k) + v (q_{k + 1} x - p_{k + 1})| = |u (q_k x - p_k)| + |v (q_{k + 1} x - p_{k + 1})|.$

Therefore, using the defining equations for u and v to substitute for p and q, I get

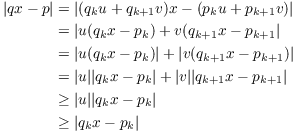
$\eqalign{ |q x - p| & = |(q_k u + q_{k + 1} v) x - (p_k u + p_{k + 1} v)| \cr & = |u (q_k x - p_k) + v (q_{k + 1} x - p_{k + 1}| \cr & = |u (q_k x - p_k)| + |v (q_{k + 1} x - p_{k + 1})| \cr & = |u| |q_k x - p_k| + |v| |q_{k + 1} x - p_{k + 1}| \cr & \ge |u| |q_k x - p_k| \cr & \ge |q_k x - p_k| \cr}$

It has been a while, but you may still remember that a hypothesis of this theorem was . So we have our contradiction, and it follows that $q \ge q_{k + 1}$ .

Corollary. Let x be irrational, and let $c_k = \dfrac{p_k}{q_k}$ be the k-th convergent in the continued fraction expansion of x. Suppose $p, q \in \integer$ , , and

$\left|x - \dfrac{p}{q}\right| < \left|x - \dfrac{p_k}{q_k}\right|.$

Then .

Proof. Given the hypotheses of the corollary, suppose on the contrary that $q \le q_k$ . Multiply this inequality by

$\left|x - \dfrac{p}{q}\right| < \left|x - \dfrac{p_k}{q_k}\right|.$

I get

$\left|q x - p\right| < \left|q_k x - p_k\right|.$

Apply the theorem to obtain $q \ge q_{k+1}$ . But then $q_k \ge q \ge q_{k+1}$ , which contradicts the fact that the q's increase.

Therefore, .

This result says that the only way a rational number $\dfrac{p}{q}$ can approximate a continued fraction better than a convergent $\dfrac{p_k}{q_k}$ is if the fraction has a bigger denominator than the convergent.

For example, consider the convergents for the continued fraction expansion of $\pi$ :

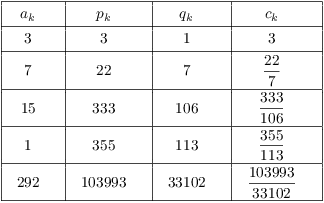
$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 1 & & 3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 7 & & 22 & & 7 & & $\dfrac{22}{7}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 15 & & 333 & & 106 & & $\dfrac{333}{106}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 355 & & 113 & & $\dfrac{355}{113}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 292 & & 103993 & & 33102 & & $\dfrac{103993}{33102}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}$

$\dfrac{355}{113} \approx 3.141592920$ , which is in error in the seventh place. The theorem says that a fraction $\dfrac{p}{q}$ can be closer to $\pi$ than $\dfrac{355}{113}$ only if .

The next result is sort of a converse to the previous two results. It says that if a rational number approximates an irrational number x "sufficiently well", then the rational number must be a convergent in the continued fraction expansion for x.

Theorem. Let x be irrational, and let $\dfrac{p}{q}$ be a rational number in lowest terms with . Suppose that

$\left|x - \dfrac{p}{q}\right| < \dfrac{1}{2 q^2}.$

Then $\dfrac{p}{q}$ is a convergent in the continued fraction expansion for x.

Proof. Since $q_k \ge k$ for $k \ge 0$ , the q's form a strictly increasing sequence of positive integers. Therefore, for some k,

$q_k \le q < q_{k+1}.$

Since $q < q_{k+1}$ , the contrapositive of the preceding theorem gives

$|q_k x - p_k| \le |q x - p| = q \cdot \left|x - \dfrac{p}{q}\right| < q \cdot \dfrac{1}{2 q^2} = \dfrac{1}{2 q}.$

Hence,

$\left|x - \dfrac{p_k}{q_k}\right| < \dfrac{1}{2 q q_k}.$

Now assume toward a contradiction that $\dfrac{p}{q}$ is not a convergent in the continued fraction expansion for x. In particular, $\dfrac{p}{q} \ne \dfrac{p_k}{q_k}$ , so $q p_k \ne p q_k$ , and hence is a positive integer.

Since $|q p_k - p q_k| \ge 1$ ,

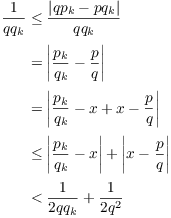
$\eqalign{ \dfrac{1}{q q_k} & \le \dfrac{|q p_k - p q_k|}{q q_k} \cr \noalign{\vskip2pt} & = \left|\dfrac{p_k}{q_k} - \dfrac{p}{q}\right| \cr \noalign{\vskip2pt} & = \left|\dfrac{p_k}{q_k} - x + x - \dfrac{p}{q}\right| \cr \noalign{\vskip2pt} & \le \left|\dfrac{p_k}{q_k} - x\right| + \left|x - \dfrac{p}{q}\right| \cr \noalign{\vskip2pt} & < \dfrac{1}{2 q q_k} + \dfrac{1}{2 q^2} \cr}$

(The second inequality comes from the Triangle Inequality: $|a + b| \le |a| + |b|$ .)

Subtracting $\dfrac{1}{2 q q_k}$ from both sides, I get

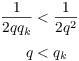
$\eqalign{ \dfrac{1}{2 q q_k} & < \dfrac{1}{2 q^2} \cr \noalign{\vskip2pt} q & < q_k \cr}$

But I assumed $q_k \le q$ , so this is a contradiction.

Therefore, $\dfrac{p}{q}$ is a convergent in the continued fraction expansion for x.

Example. Show that $\dfrac{355}{113}$ is the best rational approximation to $\pi$ by a fraction having a denominator less than 1000.

Suppose that $\dfrac{p}{q}$ is a fraction in lowest terms that is a better approximation to $\pi$ than $\dfrac{355}{113}$ , and that .

Since $\dfrac{p}{q}$ is a fraction is a better approximation to $\pi$ than $\dfrac{355}{113}$ ,

$\left|\pi - \dfrac{p}{q}\right| < \left|\pi - \dfrac{355}{113}\right|.$

Since ,

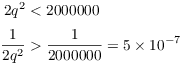
$\eqalign{ 2 q^2 & < 2000000 \cr \noalign{\vskip2pt} \dfrac{1}{2 q^2} & > \dfrac{1}{2000000} = 5 \times 10^{-7} \cr}$

But

$\left|\pi - \dfrac{355}{113}\right| = 2.66764 \ldots \times 10^{-7}.$

Thus,

$\dfrac{1}{2 q^2} > 5 \times 10^{-7} > \left|\pi - \dfrac{355}{113}\right| > \left|\pi - \dfrac{p}{q}\right|.$

The hypotheses of the theorem are satisfied, so $\dfrac{p}{q}$ must be a convergent in the continued fraction expansion of $\pi$ .

But the other convergents with denominators less than 1000 --- 3, $\dfrac{22}{7}$ , $\dfrac{333}{106}$ --- with denominators less than 1000 are poorer approximations to $\pi$ than $\dfrac{355}{113}$ .

Hence, $\dfrac{355}{113}$ is the best rational approximation to $\pi$ by a fraction having a denominator less than 1000.

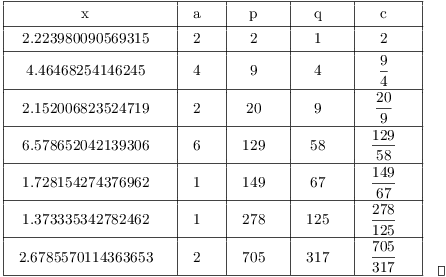
Example. (a) Compute the first 6 convergents , ... of the continued fraction for $11^{1/3}$ .

(b) Show that $\dfrac{278}{125}$ is the best rational approximation to $11^{1/3}$ having denominator less than 155.

(a)

$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & a & & p & & q & & c & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.223980090569315 & & 2 & & 2 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 4.46468254146245 & & 4 & & 9 & & 4 & & $\dfrac{9}{4}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.152006823524719 & & 2 & & 20 & & 9 & & $\dfrac{20}{9}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 6.578652042139306 & & 6 & & 129 & & 58 & & $\dfrac{129}{58}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1.728154274376962 & & 1 & & 149 & & 67 & & $\dfrac{149}{67}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1.373335342782462 & & 1 & & 278 & & 125 & & $\dfrac{278}{125}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2.6785570114363653 & & 2 & & 705 & & 317 & & $\dfrac{705}{317}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos$

(b) Suppose that $\dfrac{p}{q}$ is a fraction in lowest terms which is a better approximation to $11^{1/3}$ than $\dfrac{278}{125}$ , and also that .

Since $\dfrac{p}{q}$ is a better approximation to $11^{1/3}$ than $\dfrac{278}{125}$ ,

$\left|11^{1/3} - \dfrac{p}{q}\right| < \left|11^{1/3} - \dfrac{278}{125}\right| = 1.99094 \ldots \times 10^{-5}.$

Since ,

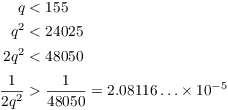
$\eqalign{ q & < 155 \cr q^2 & < 24025 \cr 2 q^2 & < 48050 \cr \noalign{\vskip2pt} \dfrac{1}{2 q^2} & > \dfrac{1}{48050} = 2.08116 \ldots \times 10^{-5} \cr}$

So I have

$\dfrac{1}{2 q^2} > 2.08116 \ldots \times 10^{-5} > 1.99094 \ldots \times 10^{-5} > \left|11^{1/3} - \dfrac{p}{q}\right|.$

(The inequalities are approximate, but there is enough room between $2.08116 \ldots \times 10^{-5}$ and $1.99094 \ldots \times 10^{-5}$ that there is no problem.)

By the approximation theorem, $\dfrac{p}{q}$ is a convergent for $11^{1/3}$ . But no convergent with is a better approximation than $\dfrac{278}{125}$ .

This contradiction shows that $\dfrac{278}{125}$ is the best rational approximation to $11^{1/3}$ having denominator less than 155.

Contact information

Bruce Ikenaga's Home Page