Arithmetic Functions

In this section, I'll derive some formulas for $\phi(n)$ . I'll also show that $\phi$ has an important property called multiplicativity. To put this in the proper context, I'll discuss arithmetic functions, Dirichlet products, and the Möbius inversion formula.

In case you prefer a more direct approach to the formulas and properties of $\phi$ , I give an alternative proof of the multiplicativity of $\phi$ in the appendix to this section.

Definition. An arithmetic function is a function defined on the positive integers which takes values in the real or complex numbers.

For instance, define $f: \integer^+ \to \real$ by $f(n) = \sin n$ . Then f is an arithmetic function.

Many functions which are important in number theory are arithmetic functions. For example:

(a) The Euler phi function $\phi$ is an arithmetic function.

(b) Define the number of divisors function $\tau: \integer^+ \to \integer^+$ by

$$\tau(n) = (\hbox{the number of positive divisors of n}).$$

For example, $\tau(12) = 6$ , since there are 6 positive divisors of 12 --- 1, 2, 3, 4, 6, and 12. $\tau$ is an arithmetic function.

(c) Define the sum of divisors function $\sigma: \integer^+ \to \integer^+$ by

$$\sigma(n) = (\hbox{the sum of the positive divisors of n}).$$

Since 1, 2, 3, 6, 9, and 18 are the positive divisors of 18,

$$\sigma(18) = 1 + 2 + 3 + 6 + 9 + 18 = 39.$$

$\sigma$ is an arithmetic function.

In order to find ways of computing $\phi(n)$ , $\tau(n)$ , and $\sigma(n)$ , we can use the following approach: First, compute the function for p, where p is prime.

Next, compute the function for $p^m$ , where p is prime and $m \ge 1$ .

Finally, for a general number n, factor n into a product of powers of primes and use the result for $p^m$ .

In order to make the jump from prime powers to an arbitrary integer, we'll show that the functions in question are multiplicative. While it's possible to do this directly for each function, we can also prove results which will allow us to use the same approach for $\phi$ , $\tau$ , and $\sigma$ . These results are important for other applications.

Definition. The Möbius function is the arithmetic function defined by $\mu(1) = 1$ , and for $n > 1$ ,

$$\mu(n) = \cases{ (-1)^k & if $n = p_i\cdots p_k$, $p_i$ distinct primes \cr 0 & otherwise \cr}.$$

Thus, $\mu(n) = 0$ if n is divisible by a square.

For example, $\mu(6) = 1$ , since $6 = 2\cdot 3$ . Likewise, $\mu(30) = -1$ , since $30 = 2 \cdot 3 \cdot 5$ . But $\mu(12) = 0$ and $\mu(250 = 0$ .

Definition. If f is an arithmetic function, the divisor sum of f is

$$[D(f)](n) = \sum_{d \mid n} f(d).$$

To save writing, I'll make the convention that when I write "$\displaystyle \sum_{d\mid n}$ ", I mean to sum over all the positive divisors of a positive integer n. Thus, the divisor sum of f evaluated at a positive integer n takes the positive divisors of n, plugs them into f, and adds up the results. A similar convention will hold for products.

Notice that the divisor sum is a function which takes an arithmetic function as input and produces an arithmetic function as output.

$$\hbox{\epsfxsize=2.5in \epsffile{arithmetic-functions-1.eps}}\hskip0.25in \hbox{\epsfxsize=2.5in \epsffile{arithmetic-functions-2.eps}}$$

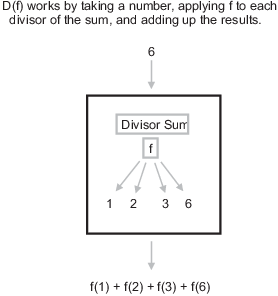
$$\hbox{\epsfxsize=2.5in \epsffile{arithmetic-functions-3.eps}}$$

Example. Suppose $f: \integer^+ \to \integer^+$ is defined by $f(n) = n^2$ . Compute $[D(f)](12)$ .

$[D(f)](n)$ is the sum of the squares of the divisors of n:

$$[D(f)](n) = \sum_{d \mid n} d^2.$$

thus,

$$[D(f)](12) = \sum_{d \mid 12} d^2 = 1^2 + 2^2 + 3^2 + 4^2 + 6^2 + 12^2 = 210.\quad\halmos$$

Lemma.

$$[D(\mu)](n) = \sum_{d \mid n} \mu(d) = \cases{ 1 & if $n = 1$ \cr 0 & otherwise \cr}$$

Proof. The formula for $n = 1$ is obvious.

Suppose $n > 1$ . Factor n into a product of powers of primes:

$$n = p_1^{r_1} \cdots p_k^{r_k}.$$

What are the nonzero terms in the sum $\displaystyle \sum_{d \mid n} \mu(d)$ ? They will come from d's which are products of single powers of $p_1$ , ... $p_k$ , and also $d = 1$ .

For example, $\mu(p_1 p_2 p_7)$ and $\mu(p_2 p_4)$ would give rise to nonzero terms in the sum, but $\mu(p_3^3 p_8) = 0$ .

So

$$\sum_{d \mid n} \mu(d) = 1 + \left(\mu(p_1) + \cdots + \mu(p_k)\right) + \left(\mu(p_1 p_2) + \mu(p_1 p_3) + \cdots + \mu(p_{k-1} p_k)\right) + \cdots + \mu(p_1 p_2 \cdots p_k) =$$

$$1 + {k \choose 1}(-1) + {k \choose 2}(-1)^2 + \cdots + {k \choose k}(-1)^k = (1 - 1)^k = 0.\quad\halmos$$

Example. Verify the previous lemma for $n = 24$ .

The divisor sum is

$$\sum_{d \mid 24} \mu(d) = \mu(1) + \mu(2) + \mu(3) + \mu(4) + \mu(6) + \mu(12) + \mu(24) = 1 + (-1) + (-1) + 0 + 1 + 0 + 0 = 0.\quad\halmos$$

Definition. If f and g are arithmetic functions, their Dirichlet product is

$$(f \ast g)(n) = \sum_{d\mid n} f(d) g\left(\dfrac{n}{d}\right).$$

For example for arithmetic functions f and g, the Dirichlet product evaluated at 12 is

$$(f \ast g)(12) = f(1) g(12) + f(2) g(6) + f(3) g(4) + f(4) g(3) + f(6) g(2) + f(12) g(1).$$

Definition. Define arithmetic functions

$$I(n) = 1 \quad\hbox{for all}\quad n \in \integer ^+,$$

$$e(n) = \cases{1 & if $n = 1$ \cr 0 & otherwise \cr} \quad\hbox{for all}\quad n \in \integer ^+.$$

Proposition. Let f, g, and h be arithmetic functions.

(a) $f \ast g = g \ast f$ .

(b) $(f \ast g) \ast h = f \ast (g \ast h)$ .

(c) $f \ast e = f = e \ast f$ .

(d) $f \ast I = Df = I \ast f$ .

(e) $\mu \ast I = e$ .

Proof. For (a), note that divisors of n come in pairs $\left\{d, \dfrac{n}{d}\right\}$ , and that if $\left\{d, \dfrac{n}{d}\right\}$ is a divisor pair, so is $\left\{\dfrac{n}{d}, d\right\}$ . This means that the same terms occur in both

$$(f \ast g)(n) = \sum_{d\mid n} f(d) g\left(\dfrac{n}{d}\right) \quad\hbox{and}\quad (g \ast f)(n) = \sum_{d\mid n} g(d) f\left(\dfrac{n}{d}\right).$$

Hence, they're equal.

Associativity is a little tedious, so I'll just note that $[(f \ast g) \ast h](n)$ and $[f \ast (g \ast h)](n)$ are equal to

$$\sum_{\{d,e,f\}} f(d) g(e) h(f).$$

Here the sum runs over all triples of positive numbers d, e, f such that $d e f = n$ . You can fill in the details.

For (c), note that

$$(f \ast e)(n) = \sum_{d \mid n} f(d) e\left(\dfrac{n}{d}\right) = f(n) e(1) = f(n).$$

($e\left(\dfrac{n}{d}\right)$ is 0 except when $\dfrac{n}{d} = 1$ , i.e. when $d = n$ .)

For (d),

$$(f \ast I)(n) = \sum_{d \mid n} f(d) I\left(\dfrac{n}{d}\right) = \sum_{d \mid n} f(d) \cdot 1 = \sum_{d \mid n} f(d) = (Df)(n).$$

For (e), start with $n = 1$ :

$$(\mu \ast I)(1) = \mu(1) I(1) = 1 \cdot 1 = 1 = e(1).$$

Now suppose $n > 1$ . Then by (d), $\mu \ast I = D\mu$ , so

$$(\mu \ast I)(n) = (D\mu)(n) = 0 = e(n).$$

Therefore, the formula holds for all n.

The next result is very powerful, but the proof will look easy with all the machinery I've collected.

Theorem. ( Möbius Inversion Formula) If f is an arithmetic function, then

$$f = \mu \ast Df.$$

Proof.

$$\mu \ast Df = \mu \ast I \ast f = e \ast f = f.\quad\halmos$$

Next, I'll compute the divisor sum of the Euler phi function.

Lemma.

$$[D(\phi)](n) = \sum_{d \mid n} \phi(d) = n.$$

Proof. Let n be a positive integer. Construct the fractions

$$\dfrac{1}{n}, \quad \dfrac{2}{n}, \ldots, \dfrac{n - 1}{n}, \quad \dfrac{n}{n}.$$

Reduce them all to lowest terms. Consider a typical lowest-term fraction $\dfrac{a}{d}$ . Here $d \mid n$ (because it came from a fraction whose denominator was n, $a < d$ (because the original fraction was less than 1), and $(a,d) = 1$ (because it's in lowest terms).

Notice that (going the other way) if $\dfrac{a}{d}$ is a fraction with positive top and bottom which satisfies $d \mid n$ , $a < d$ , and $(a,d) = 1$ , then it is one of the lowest-terms fractions. For $d k = n$ for some k, and then $\dfrac{a}{d} = \dfrac{k a}{k d} = \dfrac{k a}{n}$ --- and the last fraction is one of the original fractions.

How many of the lowest-terms fractions have "d" on the bottom? Since the "a" on top is a positive number relatively prime to d, there are $\phi(d)$ such fractions. Summing over all d's which divide n gives $\displaystyle \sum_{d \mid n} \phi(d)$ . But since every lowest-terms fraction has some such "d" on the bottom, this sum accounts for all the fractions --- and there are n of them. Therefore, $\displaystyle \sum_{d \mid n} \phi(d) = n$ .

For example, suppose $n = 6$ . Then

$$[D(\phi)](6) = \sum_{d \mid 6} \phi(d) = \phi(1) + \phi(2) + \phi(3) + \phi(6) = 1 + 1 + 2 + 2 = 6.$$

Lemma. Let $n \ge 1$ .

$$\phi(n) = \sum_{d \mid n} \mu(d) \dfrac{n}{d}.$$

Proof. By Möbius inversion and the previous result,

$$\phi(n) = (\mu \ast D\phi)(n) = \sum_{d \mid n} \mu(d) D\phi\left(\dfrac{n}{d}\right) = \sum_{d \mid n} \mu(d) \dfrac{n}{d}.\quad\halmos$$

For instance, suppose $n = 6$ , so $\phi(6) = 2$ . Then

$$\sum_{d \mid 6} \mu(d) \dfrac{6}{d} = \mu(1)\cdot \dfrac{6}{1} + \mu(2)\cdot \dfrac{6}{2} + \mu(3)\cdot \dfrac{6}{3} + \mu(6)\cdot \dfrac{6}{6} =$$

$$(1)(6) + (-1)(3) + (-1)(2) + (1)(1) = 2.$$

Theorem. Let $n \ge 1$ .

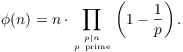
$$\phi(n) = n \cdot \prod_{{p \mid n}\atop{p\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{p}\right).$$

(By convention, the empty product --- the product with no terms --- equals 1.)

Proof. If $n = 1$ , the result is immediate by convention.

If $n > 1$ , let $p_1$ , ..., $p_k$ be the distinct prime factors of n. Then

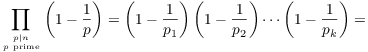
$$\prod_{{p \mid n}\atop{p\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{p}\right) = \left(1 - \dfrac{1}{p_1}\right)\left(1 - \dfrac{1}{p_2}\right) \cdots \left(1 - \dfrac{1}{p_k}\right) =$$

$$1 - \sum_i \dfrac{1}{p_i} + \sum_{i \ne j} \dfrac{1}{p_ip_j} - \cdots + (-1)^k \dfrac{1}{p_1p_2\cdots p_k}.$$

Each term is $\pm \dfrac{1}{d}$ , where d is 1 (the first term) or a product of distinct primes. The $(-1)^i$ in front of each term alternates signs according to the number of p's --- which is exactly what the Möbius function does. So the expression above is

$$\sum_{d \mid n} \dfrac{\mu(d)}{d}.$$

(I can run the sum over all divisors, because $\mu(d) = 0$ if d has a repeated prime factor.) Now simply multiply by n:

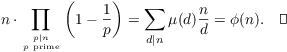
$$n \cdot \prod_{{p \mid n}\atop{p\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{p}\right) = \sum_{d \mid n} \mu(d) \dfrac{n}{d} = \phi(n).\quad\halmos$$

The formula in the theorem is useful for hand-computations of $\phi(n)$ . For example, $40 = 2^3 \cdot 5$ , so

$$\phi(40) = 40 \left(1 - \dfrac{1}{2}\right) \left(1 - \dfrac{1}{5}\right) = 16.$$

Likewise, $81 = 3^4$ , so

$$\phi(81) = 81\cdot \left(1 - \dfrac{1}{3}\right) = 54.$$

Definition. An arithmetic function f is multiplicative if $(m, n) = 1$ implies

$$f(m n) = f(m) f(n).$$

Proposition. $\phi$ is multiplicative --- that is, if $(m, n) = 1$ , then

$$\phi(m n) = \phi(m) \phi(n).$$

Proof. Suppose $(m,n) = 1$ . Now

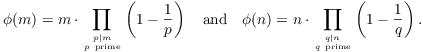
$$\phi(m) = m \cdot \prod_{{p \mid m}\atop{p\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{p}\right) \quad\hbox{and}\quad \phi(n) = n \cdot \prod_{{q \mid n}\atop{q\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{q}\right).$$

So

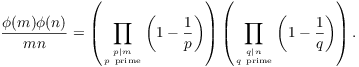
$$\dfrac{\phi(m) \phi(n)}{m n} = \left(\prod_{{p \mid m}\atop{p\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{p}\right)\right) \left(\prod_{{q \mid n}\atop{q\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{q}\right)\right).$$

Since $(m, n) = 1$ , the two products have no primes in common. Moreover, the primes that appear in either of the products are exactly the prime factors of $m n$ . So

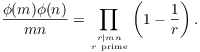
$$\dfrac{\phi(m) \phi(n)}{m n} = \prod_{{r \mid m n}\atop{r\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{r}\right).$$

Hence,

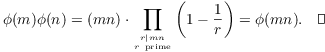
$$\phi(m) \phi(n) = (m n) \cdot \prod_{{r \mid mn}\atop{r\ \hbox{\fiverm prime}}} \left(1 - \dfrac{1}{r}\right) = \phi(m n).\quad\halmos$$

Corollary. Let $n > 1$ , and consider its prime factorization:

$$n = p_1^{r_1}\, p_2^{r_2} \cdots p_k^{r_k}.$$

(Here the p's are distinct primes, and the r's are positive integers.) Then

$$\phi(n) = (p_1^{r_1} - p_1^{r_1 - 1})\, (p_2^{r_2} - p_2^{r_2 - 1}) \cdots (p_k^{r_k} - p_k^{r_k - 1}).$$

Equivalently,

$$\phi(n) = p_1^{r_1 - 1} (p_1 - 1)\, p_2^{r_2 - 1} (p_2 - 1) \cdots p_k^{r_k - 1} (p_k - 1).$$

Proof. Note that if $i \ne j$ , then $(p_i^{r_i}, p_j^{r_j}) = 1$ . That is, the prime powers in the prime factorization of n are relatively prime. Recall that if p is prime, then

$$\phi(p^r) = p^r - p^{r - 1}.$$

These observations combined with the fact that $\phi$ is multiplicative give

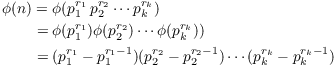
$$\eqalign{ \phi(n) & = \phi(p_1^{r_1}\, p_2^{r_2} \cdots p_k^{r_k}) \cr & = \phi(p_1^{r_1}) \phi(p_2^{r_2}) \cdots \phi(p_k^{r_k})) \cr & = (p_1^{r_1} - p_1^{r_1 - 1})(p_2^{r_2} - p_2^{r_2 - 1}) \cdots (p_k^{r_k} - p_k^{r_k - 1}) \cr}$$

The second formula follows from the first by factoring out common factors from each $p^r - p^{r - 1}$ term.

Note that in the second formula a prime power $p^r$ gives a "real" $p^{r - 1}$ term only if $r > 1$ . If $p^1$ is the highest power of p which divides n, then the corresponding term in the second formula for $\phi(n)$ is just $p - 1$ --- and so, if you don't know the value of r in $p^r$ , the only term you can assume will appear in $\phi(n)$ is $p - 1$ .

While the formula in the earlier theorem provided a way of computing $\phi(n)$ , the formula in the corollary is often useful in proving results about $\phi(n)$ .

Example. If $n \ge 3$ , then $\phi(n)$ is even. In fact, if n has k odd prime factors, then $2^k \mid \phi(n)$ .

To see this, observe first that

$$\phi(2^k) = 2^k - 2^{k-1}.$$

This is even if $2^k \ge 4$ .

So suppose that n has k odd prime factors. Each odd prime power factor $p^r$ in the prime factorization of n gives a term $p^r - p^{r - 1}$ in the product for $\phi(n)$ in the corollary, and each term $p^r - p^{r - 1}$ is even (since it's a difference of odd numbers).

Hence, $\phi(n)$ is divisible by $2^k$ .

For example, consider $7623 = 3^2 \cdot 7 \cdot 11^2$ . There are 3 odd prime factors, so $\phi(7623)$ should be divisible by 8. And in fact, $\phi(7623) = 3960 = 8 \cdot 495$ .

Example. Find all positive integers n such that $\phi(n) = 8$ .

I'll do this in steps. First, I'll show that no prime $\ge 7$ can divide n.

At that point, with $n = 2^a \cdot 3^b \cdot 5^c$ , I'll get bounds on a, b, and c. That will leave me with 16 cases, which I can check directly.

Step 1. No prime greater than 7 divides n.

Suppose $p > 7$ and the prime power $p^r$ occurs in the prime factorization of n. The formula in the second corollary tells us that there is at least a term $p - 1$ in the product for $\phi(n)$ . But since $p > 7$ , I know that p is at least 11 (the next larger prime). Thus, $p \ge 11$ , and so $p - 1 \ge 10$ . Then

$$8 = \phi(n) = (p - 1) (\hbox{other terms}) \ge 10 \cdot (\hbox{other terms}) \ge 10.$$

This is a contradiction, since the right side is larger than 8. Hence, no prime greater than 7 can divide n.

Step 2. $7 \notdiv n$ .

If $7 \mid n$ , then the formula in the second corollary tells us that there is at least a term $7 - 1 = 6$ in the product for $\phi(n)$ . So I have

$$8 = \phi(n) = 6 \cdot (\hbox{other terms}).$$

This is a contradiction, since $6 \notdiv 8$ .

At this point, I know that $n = 2^a\, 3^b\, 5^c$ .

Step 3. $a \le 4$ and $b \le 1$ and $c \le 1$ .

I have

$$8 = \phi(n) = 2^{a - 1} (2 - 1) 3^{b - 1} (3 - 1) 5^{c - 1} (5 - 1).$$

Suppose $a \ge 5$ . The factor $2^{a - 1}$ is at least $2^4 = 16$ , but $16 > 8$ . Hence, $a \le 4$ .

Suppose $b \ge 2$ . The factor $3^{b - 1}$ is at least $3^1$ , so 3 divides the right side. But $3 \notdiv 8$ . Hence, $b \le 1$ .

Suppose $c \ge 2$ . The factor $5^{c - 1}$ is at least $5^1$ , so 5 divides the right side. But $5 \notdiv 8$ . Hence, $c \le 1$ .

At this point, I know $a = 0, 1, 2, 3$ and $b = 0, 1$ and $c = 0, 1$ . I could probably eliminate some possibilities by additional analysis, but with $4 \cdot 2 \cdot 2 = 16$ cases, I can just check by hand.

Step 4. Check the remaining cases by hand.

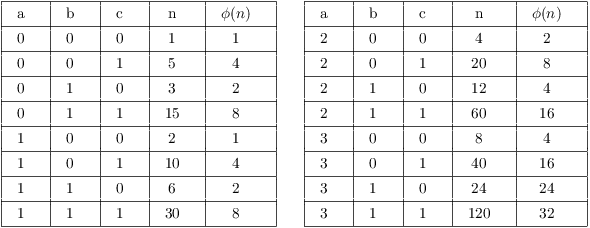
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & b & & c & & n & & $\phi(n)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 5 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 1 & & 0 & & 3 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 1 & & 1 & & 15 & & 8 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 0 & & 2 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 10 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 0 & & 6 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & 30 & & 8 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.25in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & b & & c & & n & & $\phi(n)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 0 & & 4 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 1 & & 20 & & 8 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 1 & & 0 & & 12 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 1 & & 1 & & 60 & & 16 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 0 & & 0 & & 8 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 0 & & 1 & & 40 & & 16 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 0 & & 24 & & 24 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & & 120 & & 32 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The numbers are 15, 20, 24, 30.

Appendix: An alternate proof of multiplicativity for $\phi(n)$

In this appendix, I'll give a direct proof of the multiplicativity of $\phi(n)$ which doesn't use any results on arithmetic functions.

Theorem. If $(m, n) = 1$ , then

$$\phi(m n) = \phi(m) \phi(n).$$

Proof. I list the numbers from 1 to $m n$ and count the number that are relatively prime to $m n$ .

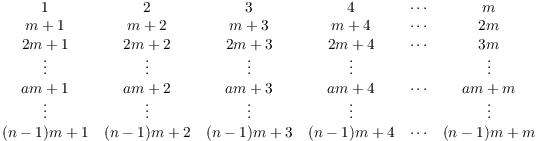
$$\matrix{ 1 & 2 & 3 & 4 & \cdots & m \cr m + 1 & m + 2 & m + 3 & m + 4 & \cdots & 2 m \cr 2 m + 1 & 2 m + 2 & 2 m + 3 & 2 m + 4 & \cdots & 3 m \cr \vdots & \vdots & \vdots & \vdots & & \vdots \cr a m +1 & a m + 2 & a m + 3 & a m + 4 & \cdots & a m + m \cr \vdots & \vdots & \vdots & \vdots & & \vdots \cr (n - 1) m +1 & (n - 1) m + 2 & (n - 1) m + 3 & (n - 1) m + 4 & \cdots & (n - 1) m + m \cr}$$

A typical column looks like:

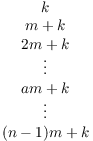
$$\matrix{k \cr m + k \cr 2 m + k \cr \vdots \cr a m + k \cr \vdots \cr (n - 1) m + k \cr}$$

Note that $(m, k)$ divides all the numbers in this column. Moreover, $(m, k) \mid m \mid m n$ . Thus, if $(m, k) \ne 1$ , then $(m, k)$ is a nontrivial divisor of each number in this column and of $m n$ .

Hence, if $(m, k) \ne 1$ , all the numbers in this column are not relatively prime to $m n$ .

Therefore, since I'm counting numbers that are relatively prime to $m n$ , I need only consider columns where $(m, k) = 1$ . There are $\phi(m)$ such columns.

So consider a column where $(m, k) = 1$ . It contains the numbers

$$\{k,\ m + k,\ 2 m + k, \ldots (n - 1) m + k\}.$$

Start with $\{0, 1, 2, \ldots n - 1\}$ , the standard residue system mod n. Since $(m, n) = 1$ , multiplying by m produces another complete residue system:

$$\{0,\ m,\ 2 m, \ldots (n - 1) m\}.$$

Adding k must also give a complete residue system:

$$\{k,\ m + k,\ 2 m + k, \ldots (n - 1) m + k\}.$$

This is the column in question, so I've shown that such a column is a complete residue system mod n. It follows that $\phi(n)$ of these numbers are relatively prime to n.

Thus, I have $\phi(m)$ columns, all of whose elements are relatively prime to m, and in each such column $\phi(n)$ of the elements are relatively prime to n. Thus, there are $\phi(m) \phi(n)$ numbers in $\{1, 2, \ldots m n\}$ which are relatively prime to $m n$ .

Let's look at how the proof works with a specific example. Take $m = 9$ and $n = 4$ . List the numbers from 1 to 36:

$$\matrix{ 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \cr 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \cr 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 \cr 28 & 29 & 30 & 31 & 32 & 33 & 34 & 35 & 36 \cr}$$

You can see that the columns beginning with 3, 6, and 9 --- the numbers k with $(9, k) \ne 1$ --- contain only numbers that are not relatively prime to 9 (and hence, are not relatively prime to 36). Removing these columns, I have $\phi(9) = 6$ columns left: The ones beginning with 1, 2, 4, 5, 7, and 8.

Pick any one of those columns --- say the one beginning with 7, which contains $\{7, 16, 25, 34\}$ . Note that these numbers reduce mod 4 to $\{3, 0, 1, 2\}$ , which is a complete residue system mod 4. And exactly $\phi(4) = 2$ of these numbers --- in this case, 7 and 25 --- are relatively prime to 4.

Thus, there are $\phi(9) \phi(4) = 6 \cdot 2 = 12$ numbers in $\{1, 2, \ldots 36\}$ which are relatively prime to $9 \cdot 4 = 36$ , and so $\phi(9 \cdot 4) = \phi(9) \phi(4)$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga