Divisibility

If a and b are integers, a divides b if there is an integer c such that

$$a c = b.$$

The notation $a \mid b$ means that a divides b.

For example, $3 \mid 6$ , since $3\cdot 2 = 6$ . And $-2 \mid 10$ , since $(-2) \cdot (-5) = 10$ . Also, $3471 \mid 0$ , since $3471 \cdot 0 = 0$ .

Remarks. (a) Be careful not to confuse "$a \mid b$ " with "$a/b$ " or "$a \div b$ ". The notation "$a \mid b$ " is read "a divides b", which is a statement --- a complete sentence which could be either true or false. On the other hand, "$a \div b$ " is read "a divided by b". This is an expression, not a complete sentence. Compare "6 divides 18" with "18 divided by 6" and be sure you understand the difference.

(b) By this definition, "$0 \mid 0$ " ("0 divides 0") is true, since (for example) $0 \cdot 42 = 0$ . Does this violate the rule that "you can't divide by 0"?

This is not a problem, and the reason has to do with a subtle difference in terminology. The rule that "you can't divide by 0" means that 0 does not have a multiplicative inverse. In general, "dividing by x" means "multiplying by the multiplicative inverse" --- for instance, dividing by 3 is multiplying by $\dfrac{1}{3}$ .

To see that 0 can't have a multiplicative inverse $0^{-1}$ , suppose toward a contradiction that it did. A number and its multiplicative inverse (by definition) multiply to 1:

$$0 \cdot 0^{-1} = 1.$$

But any number multiplied by 0 gives 0, so

$$0 = 0 \cdot 0^{-1} = 1.$$

The contradiction "$0 = 1$ " shows that $0^{-1}$ is undefined.

The definition we gave above implies, as we noted, that "0 divides 0", but this is not the same as saying "you can divide 0 by 0". The wording is close, but different. The definition in this section defines divisibility in terms of multiplication; it is not the definition of dividing in term of multiplying by the multiplicative inverse.

This is probably more than you wanted to know about this. But if you are still bothered by it, you can adjust the definition, so that "$a \mid b$ " is only defined if $a \ne 0$ . The reason I haven't done this is because I would need to check the condition or make an assumption whenever I used the notation.

The properties in the next proposition are easy consequences of the definition of divisibility; see if you can prove them yourself.

Proposition.

(a) Every number divides 0.

(b) 1 divides everything. So does -1.

(c) Every number is divisible by itself.

Proof. (a) If $a \in \integer$ , then $a \cdot 0 = 0$ , so $a \mid 0$ .

(b) To take the case of 1, note that if $a \in \integer$ , then $1 \cdot a = a$ , so $1 \mid a$ .

(c) If $n \in \integer$ , then $n \cdot 1 = n$ , so $n \mid n$ .

Definition. An integer $n > 1$ is prime if its only positive divisors are 1 and itself. An integer $n > 1$ is composite if it isn't prime.

The first few primes are

$$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots .$$

The first few composite numbers are

$$4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, \ldots .$$

Prime numbers play an important role in number theory.

Proposition. Let $a, b, c, d \in \integer$ .

(a) If $a \mid b$ and $b \mid c$ , then $a \mid c$ .

(b) If $a \mid b$ , $a \mid c$ , and $m, n \in \integer$ , then

$$a \mid m b + n c.$$

(c) If $a \mid b$ and $c \mid d$ , then $a c \mid b d$ .

(In case you were wondering, mathematicians have different names for results which are intended to indicate their relative importance. A Theorem is a very important result. A Proposition is a result of less importance. A Lemma is a result which is primarily a step in the proof of a theorem or a proposition. Of course, there is some subjectivity involved in judging how important a result is.)

Proof. (a) Suppose $a \mid b$ and $b \mid c$ . This means that there are numbers d and e such that $a d = b$ and $b e = c$ . Substituting the first equation into the second, I get $(a d)e = c$ , or $a(d e) = c$ . This implies that $a \mid c$ .

(b) Suppose $a \mid b$ and $a \mid c$ . This means that there are numbers d and e such that $a d = b$ and $a e = c$ . Then

$$m b + n c = m a d + n a e = a(m d + n e), \quad\hbox{so}\quad a \mid m b + n c.\quad\halmos$$

(c) $a \mid b$ means $a e = b$ for some e, and $c \mid d$ means $c f = d$ for some f. Therefore,

$$b d = (a e)(c f) = (e f)(a c), \quad\hbox{so}\quad a c \mid b d.\quad\halmos$$

Part (b) says, in words, that if an integer a divides integers b and c, then a divides any linear combination of b and c.

Corollary. Suppose $a \mid b$ and $a \mid c$ .

(a) $a \mid b + c$ .

(b) $a \mid b - c$ .

(c) $a \mid m b$ for all $m \in \integer$ .

In words, (a) says that if a number divides two other numbers, it divides their sum.

(b) says that if a number divides two other numbers, it divides their difference.

(c) says that if a number divides another number, it divides any multiple of the other number.

Proof. All three parts follow from part (b) of the Proposition. For (a), take $m = 1$ and $n = 1$ . For (b), take $m = 1$ and $n = -1$ . And for (c), take $n = 0$ .

Example. Prove that if x is even, then $x^2 + 2 x + 4$ is divisible by 4.

x is even means that $2 \mid x$ .

$2 \mid x$ and $2 \mid x$ implies that $4 = 2 \cdot 2 \mid x \cdot 2 = x^2$ by part (c) of the proposition.

$2 \mid 2$ and $2 \mid x$ implies that $4 = 2 \cdot 2 \mid 2 \cdot x = 2 x$ by part (c) of the proposition.

Obviously, $4 \mid 4$ .

Then $4 \mid x^2 + 2 x$ by part (b) of the proposition, so $4 \mid (x^2 + 2x) + 4$ , again by part (b) of the proposition.

Here is an important result about division of integers. It will have a lot of uses --- for example, it's the key step in the Euclidean algorithm, which is used to compute greatest common divisors.

Theorem. ( The Division Algorithm) Let a and b be integers, with $b > 0$ .

(a) There are unique integers q and r such that

$$a = b \cdot q + r, \quad\hbox{and}\quad 0 \le r < b.$$

(b) $q = \left[\dfrac{a}{b}\right]$ .

Of course, this is just the "long division" of grade school, with q being the quotient and r the remainder.

Proof. (a) The idea is to find the remainder r using Well-Ordering. What is division? Division is successive subtraction. You ought to be able to find r by subtracting b's from a till you can't subtract without going negative. That idea motivates the construction which follows.

Look at the set of integers

$$S = \{a - b n \mid n \in \integer\}.$$

In other words, I take a and subtract all possible multiples of b.

If I choose $n < \dfrac{a}{b}$ (as I can --- there's always an integer less than any number), then $b n < a$ , so $a - b n > 0$ . This choice of n produces a positive integer $a - b n$ in S. So the subset T consisting of nonnegative integers in S is nonempty.

Since T is a nonempty set of nonnegative integers, I can apply Well-Ordering. It tells me that there is a smallest element $r \in T$ . Thus, $r \ge 0$ , and $r = a - b q$ for some q (because $r \in T$ , $T \subset S$ , and everything in S has this form).

Moreover, if $r \ge b$ , then $r - b \ge 0$ , so

$$a - b q - b \ge 0, \quad\hbox{or}\quad a - b(q + 1) \ge 0.$$

So $a - b(q + 1) \in T$ , but $r = a - b q > a - b(q + 1)$ . This contradicts my assumption that r was the smallest element of T.

All together, I now have r and q such that

$$a = b \cdot q + r, \quad\hbox{and}\quad 0 \le r < b.$$

To show that r and q are unique, suppose $r'$ and $q'$ also satisfy these conditions:

$$a = b \cdot q' + r', \quad\hbox{and}\quad 0 \le r' < b.$$

Then

$$\eqalign{ b \cdot q + r & = b \cdot q' + r' \cr b(q - q') & = r' - r \cr}$$

But r and $r'$ are two nonnegative numbers less than b, so they are less than b units apart. This contradicts the last equation, which says they are $|b(q - q')|$ units apart --- unless $|b(q - q')| = 0$ . Since $b > 0$ , this means $q - q' = 0$ , or $q = q'$ . In addition, $r' - r = 0$ , so $r = r'$ . This proves that r and q are unique.

(b) Assuming $a = b q + r$ with $0 \le r < b$ , I want to show that $q = \left[\dfrac{a}{b}\right]$ .

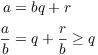
$$\eqalign{ a & = b q + r \cr \noalign{\vskip2pt} \dfrac{a}{b} & = q + \dfrac{r}{b} \ge q \cr}$$

This shows that q is an integer less than or equal to $\dfrac{a}{b}$ . Hence, $q \le \left[\dfrac{a}{b}\right]$ . I have to show that this is actually equality.

Suppose on the contrary that $q < \left[\dfrac{a}{b}\right]$ . The next integer larger than q is $q + 1$ , and $\left[\dfrac{a}{b}\right]$ must be at least as big. So

$$\eqalign{ q + 1 & \le \left[\dfrac{a}{b}\right] \cr \noalign{\vskip2pt} q + 1 + \dfrac{r}{b} & \le \left[\dfrac{a}{b}\right] + \dfrac{r}{b} \cr \noalign{\vskip2pt} b q + b + r & \le b \left[\dfrac{a}{b}\right] + r \cr}$$

Since $\left[\dfrac{a}{b}\right] \le \dfrac{a}{b}$ , the last inequality gives

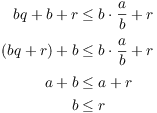
$$\eqalign{ b q + b + r & \le b \cdot \dfrac{a}{b} + r \cr \noalign{\vskip2pt} (b q + r) + b & \le b \cdot \dfrac{a}{b} + r \cr \noalign{\vskip2pt} a + b & \le a + r \cr b & \le r \cr}$$

This contradicts $0 \le r < b$ . Since $q < \left[\dfrac{a}{b}\right]$ is ruled out, I must have $q = \left[\dfrac{a}{b}\right]$ .

Example. (a) Apply the Division Algorithm to divide 59 by 7.

(b) Apply the Division Algorithm to divide -59 by 7.

(a) The quotient is $\left[\dfrac{59}{7}\right] = [8.42857 \ldots] = 8$ , the remainder is 3, and $0 \le 3 < 7$ . I have

$$59 = 8 \cdot 7 + 3.$$

(b) The quotient is $\left[\dfrac{-59}{7}\right] = [-8.42857 \ldots] = -9$ , the remainder is 4, and $0 \le 4 < 7$ . I have

$$-59 = (-9)\cdot 7 + 4.\quad\halmos$$

Example. Prove that if $n \in \integer$ , then $n^2$ does not leave a remainder of 2 or 3 when it's divided by 5.

It is easier to do this using modular arithmetic, but I'll do this using the Division Algorithm as an illustration.

If n is divided by 5, the remainder r satisifies $0 \le r < 5$ . Thus, $r = 0, 1, 2, 3, 4$ . Hence, n can have one of the following 5 forms:

$$5 q + 0, \quad 5 q + 1, \quad 5 q + 2, \quad 5 q + 3, \quad 5 q + 4.$$

Check each case:

$$n^2 = (5 q)^2 = 25 q^2 = 5(5 q^2) + 0.$$

$$n^2 = (5 q + 1)^2 = 25 q^2 + 10 q + 1 = 5(5 q^2 + 2 q) + 1.$$

$$n^2 = (5 q + 2)^2 = 25 q^2 + 20 q + 4 = 5(5 q^2 + 4 q) + 4.$$

$$n^2 = (5 q + 3)^2 = 25 q^2 + 30 q + 9 = 5(5 q^2 + 6 q + 1) + 4.$$

$$n^2 = (5 q + 4)^2 = 25 q^2 + 40 q + 16 = 5(5 q^2 + 8 q + 3) + 1.$$

In all cases, dividing $n^2$ by 5 gave a remainder of 0, 1, or 4. I never got a remainder of 2 or 3.

As an illustration, $191\,273$ can't be a perfect square, because it leaves a remainder of 3 when it's divided by 5.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga