Exponentiation Ciphers and RSA Ciphers

Exponentiation ciphers are due to Pohlig and Hellman [2]. They are less vulnerable to frequency analysis than block ciphers. Here's the procedure.

1. Let p be a prime number, and let e be the exponent, such that $(e, p - 1) = 1$ .

2. Encode the letters of the alphabet as

$$\matrix{ \hbox{A} & \hbox{B} & \cdots & \hbox{Z} \cr 00 & 01 & \cdots & 25 \cr}$$

3. Group the letters in the message in blocks of m letters, where m is chosen so that

$$\underbrace{25 25 \cdots 25}_{m \hbox{\sevenrm\ times}} < p < \underbrace{25 25 \cdots 25}_{(m + 1) \hbox{\sevenrm\ times}}$$

For example, suppose $p = 4283$ . Then you should use blocks of $m = 2$ letters, because $2525 < 4283 < 252525$ . And if $p = 670417$ , you should use blocks of $m = 3$ letters, because $252525 < 670417 < 25252525$ . This stipulation merely ensures that the blocks are unique mod p.

4. Encode a block A using

$$C = A^e \mod{p}.$$

The ciphertext C is an integer satisfying $0 \le C < p$ and this integer is the ciphertext: You don't convert it to letters.

Example. Encode the plaintext "DEEP YOGURT" using and exponential cipher with $p = 2621$ and $e = 11$ .

I have $p - 1 = 2620 = 2^2 \cdot 5\cdot 131$ . Note that $(e, p - 1) = 1$ .

I use blocks of $m = 2$ letters, because

$$2525 < 2621 < 252525.$$

Take the plaintext and convert it to numbers:

$$\matrix{ \hbox{DE} & \hbox{EP} & \hbox{YO} & \hbox{GU} & \hbox{RT} \cr 0304 & 0415 & 2414 & 0620 & 1719 \cr}$$

Now encode the message:

$$(0304)^{11} = 0065 \mod{2621}$$

$$(0415)^{11} = 0415 \mod{2621}$$

$$(2414)^{11} = 1323 \mod{2621}$$

$$(0620)^{11} = 1567 \mod{2621}$$

$$(1719)^{11} = 0150 \mod{2621}$$

The ciphertext is

$$0065\ 0415\ 1323\ 1567\ 0150$$

How should you do these computations? The best way to do the computations is to use software which can do large-integer arithmetic. Most calculators can only accomodate 10--20 digit integers. If you try to compute $2414^{11}$ on a calculator, you'll find that it's around $1.62 \times 10^{37}$ . Because these computations require modular arithmetic, you can't use floating point --- you are losing significant digits.

So how do you do something like $2414^{11}$ if all you have is a calculator? First, rewrite it:

$$2414^{11} = (2414^2)^5 \cdot 2414.$$

Now I'll compute $2414^2$ and reduce it mod 2621:

$$2414^2 = 5827396, \quad 5827396 = 913 \mod{2621}.$$

(I got the last result by finding $\dfrac{5827396}{2621} \approx 2223.34834$ . Subtract the integer part (2223) times 2621 from 5827396: $5827396 - 2223 \cdot 2621 = 913$ .)

Therefore,

$$2414^{11} = (2414^2)^5\cdot 2414 = 913^5\cdot 2414 \mod{2621}.$$

It should be clear how to proceed. Use the rules for exponents to reduce the product a little bit at a time, so that the intermediate results don't overflow your calculator.

Obviously, it is easier to use a computer!

To decode a message that has been encoded using an exponentation cipher,find d such that

$$d e = 1 \mod{p - 1}.$$

This is possible (using the Euclidean algorithm), since $(e, p - 1) = 1$ by assumption. Equivalently, for some k,

$$d e = 1 + k (p - 1).$$

Now suppose $C = A^e \mod{p}$ . Then

$$C^d = A^{d e} = A^{1 + k (p-1)} = A\cdot A^{k (p-1)} = A \cdot (A^{p-1})^k = A \cdot 1^k = A \mod{p}.$$

Note that A is less than $2525\cdots 25$ (m 25's) because A came from a block of m letters. Since $2525\cdots 25 < p$ , it follows that $p \notdiv A$ , and Fermat's theorem implies that $A^{p-1} = 1 \mod{p}$ .

In other words, raising C to the d-th power recovers the plaintext from the ciphertext.

Example. Decode the block $C = 1407$ which was encoded using an exponential cipher with $p = 2621$ and $e = 11$ .

$(2620, 11) = 1$ ; apply the Extended Euclidean algorithm:

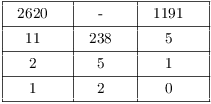
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2620 & & - & & 1191 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 11 & & 238 & & 5 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 5 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$1 = (-5) \cdot 2620 + 1191 \cdot 11.$$

Hence, $1191 \cdot 11 = 1 \mod{2620}$ .

So to decode $C = 1407$ , raise it to the 1191-th power:

$$(1407)^{1191} = 0712 \mod{2621}.$$

$0712 = \hbox{HM}$ , which is the plaintext for this block.

In a public-key cryptosystem, there are separate keys for encoding and decoding messages. One key is public, so that anyone can send a message to me. But I'm the only one who knows the private key, so I'm the only one who can read my messages. Moreover, I can use my private key to send messages, which can be decoded using the public key. Since I'm the only one who could have encoded such a message, people know the message must have come from me --- a digital signature.

The key is to come up with a one-way function: roughly, something which is easy to compute, but whose inverse is difficult to compute.

The RSA public-key cryptosystem is due to Rivest, Shamir, and Adleman [3]. You'll see that it's essentially a modified exponentiation cipher.

The idea of creating an asymmetric public-key system is due to Whitfield Diffie and Martin Hellman [1]. But they didn't explain how to implement the necessary one-way function. Clifford Cocks, a mathematician at the British intelligence agency GCHQ, had described in an internal document in 1973 a cryptographic scheme equivalent to RSA. However, it did not come to light until 1997 due to its security classification.

Actually implementing an RSA system for real-world use is tricky --- lots of things can go wrong! So you should regard what follows as a simplified description to get the main ideas across. (This is what's known as "textbook RSA".) Take a look at some recent books on cryptography to get an idea of the issues involved with implementation.

The article by Robinson [4] is recommended for an account of the creation of RSA, and a general overview.

1. Let p and q be large prime numbers. For practical applications, you'll need primes which are around 100 digits long. Let $n = pq$ . (n is called the key.)

2. Find an exponent e such that $(e, \phi(n)) = 1$ , and such that $2^e > n$ .

If n were prime, $\phi(n)$ would be $n - 1$ , and I'd have the setup for an exponentiation cipher. The condition $2^e > n$ guarantees that you can't recover the plaintext A by taking e-th roots. For if A is any block besides $0 \cdots 00$ or $0 \cdots 01$ , the result is $> n$ when it's raised to the e-th power, so it changes when it's reduced mod n.

3. Encode the letters of the alphabet as

$$\matrix{\hbox{A} & \hbox{B} & \cdots & \hbox{Z} \cr 00 & 01 & \cdots & 25 \cr}$$

4. Group the letters in the message in blocks of m letters, where m is chosen so that

$$\underbrace{25 25 \cdots 25}_{m \hbox{\sevenrm\ times}} < n < \underbrace{25 25 \cdots 25}_{(m + 1) \hbox{\sevenrm\ times}}$$

5. Encode a block A using

$$C = A^e \mod{n}.$$

Example. Encode the message "CRAB LEGS" using an RSA cipher with $n = 37 \cdot 71 = 2627$ and $e = 13$ .

$$\phi(n) = \phi(37) \phi(71) = 36 \cdot 70 = 2520.$$

Note that $e = 13$ is relatively prime to 2520, and $2^e = 8192 > 2627$ .

Since $2525 < 2627 < 252525$ , I use blocks of two letters.

Take the plaintext and convert it to numbers:

$$\matrix{ \hbox{CR} & \hbox{AB} & \hbox{LE} & \hbox{GS} \cr 0217 & 0001 & 1104 & 0618 \cr}$$

Now encode the message:

$$(0217)^{13} = 1652 \mod{2627}$$

$$(0001)^{13} = 0001 \mod{2627}$$

$$(1104)^{13} = 1400 \mod{2627}$$

$$(0618)^{13} = 1839 \mod{2627}$$

The ciphertext is

$$1652\ 0001\ 1400\ 1839\quad\halmos$$

When this system is used, e and n are made public so people can encipher messages. The security of this method depends on the difficulty of finding $\phi(n)$ , since (as I'll show below) this is what you need to decode a message.

On the one hand, if you know p and q, then

$$\phi(n) = \phi(p) \phi(q) = (p - 1)(q - 1).$$

Since p and q are known, so is $\phi(n)$ .

On the other hand, suppose you know $\phi(n)$ , you don't know p and q, but you do know that n is a product of two primes p and q. Then

$$\phi(n) = \phi(p) \phi(q) = (p - 1)(q - 1) = p q - p - q + 1 = n - p - q + 1.$$

Therefore,

$$p + q = n - \phi(n) + 1.$$

Moreover,

$$p - q = \sqrt{(p + q)^2 - 4 p q} = \sqrt{(p + q)^2 - 4n}.$$

The last two equations show that if you know $\phi(n)$ (and n), then you can find $p + q$ , and from that you can find $p - q$ . But

$$p = \left(\dfrac{1}{2}(p + q) + \dfrac{1}{2}(p - q)\right) \quad\hbox{and}\quad q = \left(\dfrac{1}{2}(p + q) - \dfrac{1}{2}(p - q)\right).$$

Thus, you know p and q.

To summarize, knowing $\phi(n)$ is equivalent to knowing p and q.

If p and q are 100-digit primes, then $n = pq$ is around 200 digits. With present technology, it's hard to factor an arbitrary 200-digit number. It follows that finding $\phi(n)$ --- and hence, breaking the code --- is difficult at the moment, which means the system is fairly secure.

Of course, no cipher is immune to human carelessness! If you let someone discover your key, the cipher is worthless.

Example. The product of two prime numbers p and q is $n = 74483$ , and $\phi(n) = 73920$ . Without factoring directly, find p and q. Show your work!

I have

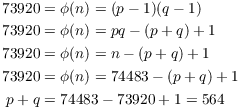
$$\eqalign{ 73920 & = \phi(n) = (p - 1)(q - 1) \cr 73920 & = \phi(n) = p q - (p + q) + 1 \cr 73920 & = \phi(n) = n - (p + q) + 1 \cr 73920 & = \phi(n) = 74483 - (p + q) + 1 \cr p + q & = 74483 - 73920 + 1 = 564 \cr}$$

Also

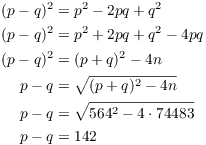
$$\eqalign{ (p - q)^2 & = p^2 - 2 p q + q^2 \cr (p - q)^2 & = p^2 + 2 p q + q^2 - 4 p q \cr (p - q)^2 & = (p + q)^2 - 4 n \cr p - q & = \sqrt{(p + q)^2 - 4 n} \cr p - q & = \sqrt{564^2 - 4 \cdot 74483} \cr p - q & = 142 \cr}$$

From $p + q = 564$ and $p - q = 142$ I get $p = 353$ and $q = 211$ .

Now here's how knowing $\phi(n)$ allows you to decode a message. The idea is similar to that used in the exponentiation cipher.

Find d such that

$$d e = 1 \mod{\phi(n)}.$$

This is possible (using the Euclidean algorithm), since $(e, \phi(n)) = 1$ by assumption. Equivalently, $de = 1 + k\phi(n)$ for some k. Now suppose $C = A^e \mod{n}$ . Then

$$C^d = A^{d e} = A^{1 + k \phi(n)} = A\cdot A^{k \phi(n)} = A \cdot (A^{\phi(n)})^k = A \cdot 1^k = A \mod{n}.$$

$A^{\phi(n)} = 1$ is a consequence of Euler's theorem, and will be true provided $(A, n) = 1$ . Now $n = pq$ , so it's possible for this to fail if the plaintext A has either p or q as a prime factor. However, if p and q are each around 100 digits long, the probability that this will happen is around $10^{-99}$ --- so it's nothing to worry about.

Just as in the exponentiation cipher, raising C to the d-th power recovers the plaintext from the ciphertext.

Example. Take $n = 2627$ and $e = 13$ . Show that 2114 is not an enciphered message by decoding it.

Recall that $\phi(2627) = 2520$ . Apply the Extended Euclidean algorithm:

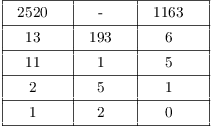
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2520 & & - & & 1163 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 13 & & 193 & & 6 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 11 & & 1 & & 5 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 5 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$(6)(2520) + (-1163)(13) = 1, \quad\hbox{so}\quad (-1163)(13) = 1 \mod{2520}, \quad\hbox{and}\quad 1357\cdot 13 = 1 \mod{2520}.$$

Then

$$(2114)^{1357} = 1980 \mod{2627}.$$

However, 80 can't be a block in a message, because it's greater than 25. Therefore, 2114 is not a ciphertext for this key.

[1] W. Diffie and M. Hellman, New directions in cryptography, IEEE Trans. Inf. Theory, 22(1976), 644--654.

[2] S. Pohlig and M. Hellman, An improved algorithm for computing logarithms over $GF(p)$ and its cryptographic significance, IEEE Trans. Inf. Theory, 24(1978), 106--110.

[3] Rivest, R.; Shamir, A.; Adleman, L., A method for obtaining digital signatures and public-key cryptosystems, Communications of the ACM, 21(2)(1978), 120--126.

[4] S. Robinson, Still guarding secrets after years of attacks, RSA earns accolades for its founders, SIAM News, 36(5)(2003).

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga