Greatest Common Divisors

Definition. The greatest common divisor of two integers (not both zero) is the largest integer which divides both of them.

If a and b are integers (not both 0), the greatest common divisor of a and b is denoted $(a, b)$ .

(The greatest common divisor is sometimes called the greatest common factor or highest common factor.)

Here are some easy examples:

$$(4, 6) = 2, \quad (17, 17) = 17, \quad (42, 0) = 42, \quad (12, -15) = 3.$$

You were probably able to do the last examples by factoring the numbers in your head. For instance, to find $(4, 6)$ , you see that 2 is the only integer bigger than 1 which divides both 4 and 6.

The problem with this approach is that it requires that you factor the numbers. However, once the numbers get too large --- currently, "too large" means "on the order of several hundred digits long" --- this approach to finding the greatest common divisor won't work. Fortunately, the Euclidean algorithm computes the greatest common divisor of two numbers without factoring the numbers. I'll discuss it after I state and prove some elementary properties.

Proposition. Let a and b be integers, not both 0.

(a) $(a, b) \ge 1$ .

(b) $(a, b) = (|a|, |b|)$ .

(c) $(a, b) = (a + k b, b)$ for any integer k.

Proof. (a) Since $1 \mid a$ and $1 \mid b$ , $(a, b)$ must be at least as big as 1.

(b) $x \mid a$ if and only if $x \mid -a$ ; that is, a and $-a$ have the same factors. But $|a|$ is either a or $-a$ , so a and $|a|$ have the same factors. Likewise, b and $|b|$ have the same factors. Therefore, x is a common factor of a and b if and only if it's a common factor of $|a|$ and $|b|$ . Hence, $(a, b) = (|a|,|b|)$ .

(c) First, if x is a common factor of a and b, then $x \mid a$ and $x \mid b$ . Then $x \mid kb$ , so $x \mid a + k b$ . Thus, x is a common factor of $a + k b$ and b.

Likewise, if x is a common factor of $a + k b$ and b, then $x \mid a + k b$ and $x \mid b$ . Hence,

$$x \mid (a + kb) - kb = a.$$

Thus, x is a common factor of a and b.

Therefore, these two sets are the same:

$$\left\{\matrix{ \hbox{common factors} \cr \hbox{of a and b} \cr}\right\} = \left\{\matrix{ \hbox{common factors} \cr \hbox{of $a + kb$ and b} \cr}\right\}.$$

Since the two sets are the same, their largest elements are the same. The largest element of the first set is $(a, b)$ , while the largest element of the second set is $(a + kb, b)$ . Therefore, $(a, b) = (a + k b, b)$ .

Example. Use the property $(a, b) = (a + k b, b)$ to compute $(998, 996)$ .

Part (c) of the proposition says that the greatest common divisor remains unchanged if you add or subtract a multiple of one of the numbers from the other. You can often use this to simplify computations of greatest common divisors. For example,

$$(998, 996) = (998 - 996, 996) = (2, 996).$$

Now $(2, 996) \mid 2$ , and the only positive integers which divide 2 are 1 and 2. So $(2, 996)$ is either 1 or 2. But 2 and 996 are obviously both divisible by 2, so $(2, 996) = 2$ . Therefore, $(998, 996) = 2$ .

Example. Prove that if $n \in \integer$ , then $(3n + 4, n + 1) = 1$ .

By part (c) of the proposition,

$$(3n + 4, n + 1) = \left((3n + 4) - 3(n + 1), n + 1\right) = (1, n + 1).$$

Now $(1, n + 1) \mid 1$ , but the only positive integer which divides 1 is 1. So $(1, n + 1) = 1$ , and hence $(3n + 4, n + 1) = 1$ .

Definition. a and b are relatively prime if $(a, b) = 1$ .

For example, 49 and 54 are relatively prime, but 25 and 105 are not.

Proposition. If $d = (m, n)$ , then $\left(\dfrac{m}{d}, \dfrac{n}{d}\right) = 1$ .

Proof. Suppose $m = da$ and $n = db$ . Then

$$\left(\dfrac{m}{d}, \dfrac{n}{d}\right) = (a, b).$$

Suppose that $p > 0$ and $p \mid a$ , $p \mid b$ . Then I can find e and f such that

$$a = p e \quad\hbox{and}\quad b = p f.$$

Thus,

$$m = d p e \quad\hbox{and}\quad n = d p f.$$

This shows that $dp$ is a common factor of m and n. Since d is the greatest common factor, $d \ge dp$ . Therefore, $1 \ge p$ , so $p = 1$ (since p was a positive integer).

I've proven that 1 is the only positive common factor of a and b. Therefore, 1 is the greatest common factor of a and b:

$$\left(\dfrac{m}{d},\dfrac{n}{d}\right) = (a, b) = 1.\quad\halmos$$

Euclidean Algorithm. Begin with a pair of nonnegative integers $\{m, n\}$ , not both 0.

(The absolute value property I stated earlier shows that there's no harm in assuming the integers are nonnegative.)

1. If one of the numbers is 0, the other is the greatest common divisor of the pair. (Stop.)

2. Otherwise, apply the Division Algorithm to write $m = q n + r$ , where $0 \le r < n$ .

3. Replace the pair $\{m, n\}$ with the pair $\{n, r\}$ .

4. Go to step 1.

At each step, both elements are $\ge 0$ , and each pass through step 3 decreases the second element. Since the second element always gets smaller, but can't be negative, Well-Ordering implies that algorithm must terminate in an $\{x , 0\}$ pair (in step 2) after a finite number of steps.

I get the next pair of numbers by subtracting a multiple of one of the previous numbers from the other. Therefore, each pair of numbers has the same greatest commmon divisor as the previous pair. Considering the whole chain of pairs, it follows that the original pair of numbers and the last pair of numbers have the same greatest common divisor.

The original pair of numbers is $\{m, n\}$ , and their greatest common divisor is $(m, n)$ . The last pair of numbers is $\{x, 0\}$ and $(x, 0) = x$ . Thus, $(m, n) = x$ --- in words, the greatest common divisor is the last nonzero remainder.

Example. Use the Euclidean algorithm to compute $(124, 348)$ .

Here what the algorithm above says. You start with the original numbers. Think of them as the first two "remainders". At each step, you divide the next-to-the-last remainder by the last remainder. You stop when you get a remainder of 0. Here are the divisions:

$$348 = 2 \cdot 124 + 100,$$

$$124 = 1 \cdot 100 + 24,$$

$$100 = 4 \cdot 24 + 4,$$

$$24 = 6 \cdot 4 + 0.$$

(Start by dividing the bigger number by the smaller number, or else you'll just waste a step.)

It's easier to remember this visually by arranging the computations in a table. Compare the numbers above to the numbers in the following table:

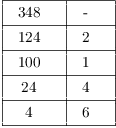
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 348 & & - & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 124 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 100 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 24 & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & 6 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

(The next remainder is 0, so I didn't write it.) The successive remainders go in the a-column. The successive quotients go in the q-column.

The greatest common divisor is the last nonzero remainder, so $(348, 124) = 4$ .

Later on, I'll add another column to this table when I discuss the Extended Euclidean algorithm.

Example. Compute $(482, 288)$ .

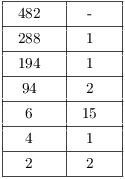
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 482 & & - & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 288 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 194 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 94 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 6 & & 15 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

From the table, I see that $(482, 288) = 2$ .

To compute the greatest common divisor of more than two divisors, just compute the greatest common divisor two numbers at a time.

Example. Compute $(42, 105, 91)$ .

$$(42, 105) = 21, \quad\hbox{so}\quad (42, 105, 91) = ((42, 105), 91) = (21, 91) = 7.\quad\halmos$$

The next result is extremely important, and is often used in proving things about greatest common divisors. First, I'll recall a definition from linear algebra.

Definition. If x and y are numbers, a linear combination of x and y (with integer coefficients) is a number of the form

$$a x + b y, \quad\hbox{where}\quad a, b \in \integer.$$

For instance, $29 = 2 \cdot 10 + 1 \cdot 9$ shows that 29 is a linear combination of 10 and 9. $7 = (-2) \cdot 10 + 3 \cdot 9$ shows that 7 is a linear combination of 10 and 9 as well.

Theorem. $(m, n)$ is the smallest positive linear combination of m and n. In particular, there are integers a and b (not necessarily unique) such that

$$(m, n) = a m + b n.$$

For example, I showed above that $(348, 124) = 4$ . The theorem says that there are integers a and b such that

$$4 = a \cdot 348 + b \cdot 124.$$

In fact,

$$4 = 5 \cdot 348 + (-14) \cdot 124.$$

This combination is not unique. For example,

$$4 = 129 \cdot 348 + (-362) \cdot 124.$$

We'll discuss later how you find numbers which give a linear combination.

I'll give a few easy corollaries before proving the theorem.

Corollary. The set of all linear combinations of integers m and n is the set of all multiples of $(m, n)$ .

Proof. On the one hand,

$$(m, n) \mid a m + b n.$$

So every linear combination of m and n is a multiple of $(m, n)$ .

On the other hand,

$$(m, n) = a m + b n, \quad\hbox{so}\quad k (m, n) = (a k) m + (b k) n.$$

That is, every multiple of $(m, n)$ is a linear combination of m and n.

Let's look at some specific numbers. I have $(42, 105) = 21$ , so the theorem asserts that the set of all linear combinations of 42 and 105 --- that is, the set of all numbers of the form $42 a + 105 b$ --- is the set of all multiples of 21:

$$\ldots, -42, -21, 0, 21, 42, 63, \ldots .$$

Notice that the greatest common divisor is the smallest positive element of this set.

If you know a little group theory, you may recognize this as the result that subgroups of cyclic groups are cyclic.

Corollary. If $d \mid m$ and $d \mid n$ , then $d \mid (m, n)$ .

Proof.

$$(m, n) = a m + b n \quad\hbox{for some}\quad a, b \in \integer.$$

Therefore, $d \mid m$ and $d \mid n$ , then $d \mid (a m + b n) = (m, n)$ .

This says that the greatest common divisor is not only "greatest" in terms of size; it's also "greatest" in the sense that any other common factor must divide it.

Corollary. m and n are relatively prime if and only if

$$a m + b n = 1 \quad\hbox{for some}\quad a, b \in \integer.$$

Proof. ($\Rightarrow$ ) Suppose m and n are relatively prime. Then $(m, n) = 1$ . By the theorem,

$$(m, n) = a m + b n \quad\hbox{for some}\quad a, b \in \integer.$$

Therefore,

$$a m + b n = 1 \quad\hbox{for some}\quad a, b \in \integer.$$

($\Leftarrow$ ) Suppose

$$a m + b n = 1 \quad\hbox{for some}\quad a, b \in \integer.$$

Since $(m, n) \mid m$ and $(m, n) \mid n$ ,

$$(m, n) \mid a m + b n = 1.$$

The only positive integer that divides 1 is 1, so $(m, n) = 1$ .

Example. Prove that if $n \in \integer$ , then $(3 n + 17, 2 n + 11) = 1$ .

I'll produce a linear combination of $3 n + 17$ and $2 n + 11$ which is equal to 1. An easy thing to try is to switch the "3" and "2" and negate one of them, in order to get the terms with n to cancel. In fact, that works:

$$2 (3 n + 17 ) - 3 (2 n + 11) = 1.$$

Note: You can't always do this kind of "switch and negate" trick: Sometimes coming up with a linear combination is more work. And there are other ways to show two numbers are relatively prime.

Proof of the theorem. I'll use the Euclidean algorithm. At each step in the Euclidean algorithm, I replace an old pair of numbers with a new pair of numbers. The proof will go this way.

(a) The first two numbers m and n are linear combinations of m and n.

(b) At each step, if the old numbers are linear combinations of m and n, then so are the new numbers.

(c) By (a) and (b), the last two numbers in the algorithm must be linear combinations of m and n.

(d) The last two numbers in the algorithm are $(m, n)$ and 0. Therefore, $(m, n)$ is a linear combination of m and n.

Of these four steps, all are clear except the second. So here is the proof of step (b).

Suppose that my old numbers are $\{x, y\}$ , and suppose that they're linear combinations of m and n:

$$x = a m + b n \quad\hbox{and}\quad y = c m + d n.$$

To do the Euclidean algorithm I divide x by y:

$$x = q y + r, \quad\hbox{where}\quad 0 \le r < y.$$

The new numbers are

$$\{y, r\} = \{y, x - q y\} = \{c m + d n, (a m + b n) - q(c m + d n)\} = \{c m + d n, (a - q c)m + (b - q d)n\}.$$

Each of the new numbers is a linear combination of m and n.

This proves step (b), and the four steps above show that $(m, n)$ is a linear combination of m and n. Next, I have to show that it's the smallest positive linear combination of m and n.

Suppose p is a positive linear combination of m and n:

$$p = a m + b n \quad\hbox{for some}\quad a, b \in \integer.$$

$(m, n) \mid m$ and $(m, n) \mid n$ , so $(m, n) \mid p$ . Both of these numbers are positive, so $(m, n) \le p$ . Since $(m, n)$ is smaller than any positive linear combination of m and n, $(m, n)$ must be the smallest positive linear combination of m and n.

Another way to prove this result is to give an algorithm which constructs a linear combination: the Extended Euclidean Algorithm.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga