Induction

Mathematical induction is a method for proving a result which consists of a sequence of statements:

$$\hbox{statement}_1, \hbox{statement}_2, \hbox{statement}_3, \ldots .$$

It applies when the statements in the sequence are related or similar. The idea is that if you can get started, and if you can make each step from one statement to the next, you can prove all of them. Induction depends on the following fundamental property of the positive integers:

Axiom. (Well-Ordering) Every nonempty set of positive integers has a smallest element.

This may seem obvious, and it is. There is no question of proving the Well-Ordering Principle; it's essentially an axiom which defines the positive integers. As simple as it sounds, it has very important consequences: Induction, which I'll discuss here, is one, and the Division Algorithm is another.

Induction will work like this. Suppose you have a sequence of statements:

$$\hbox{statement}_1, \hbox{statement}_2, \hbox{statement}_3, \ldots.$$

Sometimes the first statement will be $\hbox{statement}_0$ rather than $\hbox{statement}_1$ . The numbering can start with any integer, but often the first statement is numbered 0 or 1.

First, do the basis step:

1. Prove the first statement --- let's say that it's $\hbox{statement}_1$ .

(Sometimes the basis step involves proving more than one statement. I'll give an example of this later.)

Next, do the induction step:

2. Assume $\hbox{statement}_n$ is true, and try to prove $\hbox{statement}_{n+1}$ .

When you've completed both steps, all the statements $\hbox{statement}_1$ , $\hbox{statement}_2$ , $\hbox{statement}_3$ , ... are true, by induction.

The statement $\hbox{statement}_n$ which you're assuming to be true is called the induction hypothesis or induction assumption.

The procedure I've given is often called simple induction. You may also do a general induction (also called a strong induction), in which case the induction step above is replaced by:

2'. Assume that $\hbox{statement}_1$ , $\hbox{statement}_2$ , ..., $\hbox{statement}_n$ are true, and try to prove $\hbox{statement}_{n+1}$ .

That is, in simple induction you assume the last statement is true and try to prove the next statement. In general induction, you assume that all the preceding statements are true, and try to prove the next statement. Which one you use depends on the situation.

Remarks. The labelling of the statements is arbitrary, so some people prefer to do the induction step this way:

2. Assume $\hbox{statement}_{n-1}$ is true, and try to prove $\hbox{statement}_n$ .

In this case, the induction step for a general or strong induction would be:

2'. Assume that $\hbox{statement}_1$ , $\hbox{statement}_2$ , ..., $\hbox{statement}_{n-1}$ are true, and try to prove $\hbox{statement}_n$ .

Also, the first statement in the sequence need not be statement 1; it could be statement 0, or statement 5. The numbering depends on the situation.

Before I give some examples, let me explain how induction is related to well-ordering. Why does proving the basis and induction steps prove that all the statements in the sequence are true?

Consider the case of a simple induction.

Well, if not all the statements are true, there must be a first statement which is false. Why? The numbers of the false statements form a subset of the positive integers, so by Well-Ordering, this subset has the smallest element. This smallest element is the number of the first false statement.

Suppose the first false statement is $\hbox{statement}_{\rm false}$ . Then the statement before it ($\hbox{statement}_{{\rm false} - 1}$ ) is true. There must be some true statement before $\hbox{statement}_{\rm foo}$ , because I've proved $\hbox{statement}_1$ is true in the basis step.

But the induction step shows if a statement is true, then the next statement is true. Applying this to the true statement $\hbox{statement}_{{\rm false} - 1}$ tells me that $\hbox{statement}_{\rm false}$ is true --- which contradicts the fact that it's false.

This contradiction shows that there can't be any false statements, so all the statements in the sequence must be true.

Here are some examples of induction proofs.

Example. Show that

$$\sum_{k = 1}^n k = \dfrac{n(n + 1)}{2} \quad\hbox{for}\quad n \ge 1.$$

Here's a geometric argument which makes the result plausible.

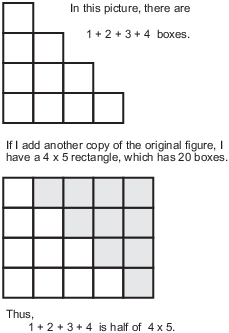
$$\hbox{\epsfysize=3in \epsffile{induction1.eps}}$$

The example shows that in general, $1 + 2 + \cdots + n$ boxes should be half of an n by $n + 1$ rectangle.

However convincing the pictures may be, they aren't really a proof. I'll prove the result using induction.

First, I prove the result for $n = 1$ . Plugging $n = 1$ into the formula, I find that

$$\sum_{k = 1}^1 k = 1 \quad\hbox{while}\quad \dfrac{1 \cdot (1 + 1)}{2} = 1.$$

It's true for $n = 1$ .

I'll use the first form of the induction step. Assume the result is true for n:

$$\sum_{k = 1}^n k = \dfrac{n(n + 1)}{2}.$$

Note that I'm assuming that this is true! I want to prove the next statement, which is the statement for $n + 1$ :

$$\sum_{k = 1}^{n+1} k = \dfrac{(n + 1)(n + 2)}{2}.$$

Start with the thing you know to be true.

$$\sum_{k = 1}^n k = \dfrac{n(n + 1)}{2}.$$

Add n to both sides:

$$\sum_{k = 1}^n k + (n + 1) = \dfrac{n(n + 1)}{2} + (n + 1).$$

The left side is the sum from 1 to $n + 1$ , so

$$\sum_{k = 1}^{n+1} k = \dfrac{n(n + 1)}{2} + (n + 1).$$

Combine the terms on the right over a common denominator:

$$\sum_{k = 1}^{n+1} k = \dfrac{n(n + 1)}{2} + (n + 1) = \dfrac{n(n + 1) + 2(n + 1)}{2} = \dfrac{n^2 + n + 2 n + 2}{2} = \dfrac{n^2 + 3 n + 2}{2} = \dfrac{(n + 1)(n + 2)}{2}.$$

This is the statement for $n + 1$ , which is what I wanted to prove. By induction, the result is true for all $n \ge 1$ .

Example. Prove that for $n \ge 1$ ,

$$\dfrac{1}{4 \cdot 7} + \dfrac{1}{7 \cdot 10} + \cdots + \dfrac{1}{(3 n + 1)(3 n + 4)} = \dfrac{n}{4 (3 n + 4)}.$$

For $n = 1$ , the left side is $\dfrac{1}{4 \cdot 7} = \dfrac{1}{28}$ and the right side is $\dfrac{1}{4 \cdot 7} = \dfrac{1}{28}$ . The result holds for $n = 1$ .

Assume that the result is true for n:

$$\dfrac{1}{4 \cdot 7} + \dfrac{1}{7 \cdot 10} + \cdots + \dfrac{1}{(3 n + 1)(3 n + 4)} = \dfrac{n}{4 (3 n + 4)}.$$

Prove the result for $n + 1$ :

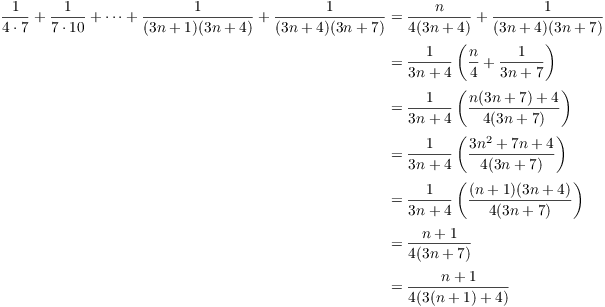
$$\eqalign{ \dfrac{1}{4 \cdot 7} + \dfrac{1}{7 \cdot 10} + \cdots + \dfrac{1}{(3 n + 1)(3 n + 4)} + \dfrac{1}{(3 n + 4)(3 n + 7)} & = \dfrac{n}{4 (3 n + 4)} + \dfrac{1}{(3 n + 4)(3 n + 7)} \cr \noalign{\vskip2pt} & = \dfrac{1}{3 n + 4} \left(\dfrac{n}{4} + \dfrac{1}{3 n + 7}\right) \cr \noalign{\vskip2pt} & = \dfrac{1}{3 n + 4} \left(\dfrac{n (3 n + 7) + 4}{4 (3 n + 7)}\right) \cr \noalign{\vskip2pt} & = \dfrac{1}{3 n + 4} \left(\dfrac{3 n^2 + 7 n + 4}{4 (3 n + 7)}\right) \cr \noalign{\vskip2pt} & = \dfrac{1}{3 n + 4} \left(\dfrac{(n + 1)(3 n + 4)}{4 (3 n + 7)}\right) \cr \noalign{\vskip2pt} & = \dfrac{n + 1}{4 (3 n + 7)} \cr \noalign{\vskip2pt} & = \dfrac{n + 1}{4 (3 (n + 1) + 4)} \cr}$$

This proves the result for $n + 1$ , so the result holds for all $n \ge 1$ by induction.

Example. Prove that if $n \ge 5$ , then $3^n > (n + 1)^3$ .

For $n = 5$ , I have $3^n = 3^5 = 243$ and $(n + 1)^3 = 6^3 = 216$ . The result is true for $n = 5$ .

Assume that the result is true for n:

$$3^n > (n + 1)^3.$$

I'll try to prove the result for $n + 1$ :

$$3^{n + 1} > (n + 2)^3.$$

In order to see better what I'm trying to prove, I'll expand $(n + 2)^3$ :

$$(n + 2)^3 = n^3 + 6 n^2 + 12 n + 8.$$

Now I'll start the proof:

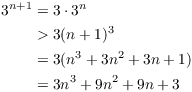
$$\eqalign{ 3^{n + 1} & = 3 \cdot 3^n \cr & > 3 (n + 1)^3 \cr & = 3 (n^3 + 3 n^2 + 3 n + 1) \cr & = 3 n^3 + 9 n^2 + 9 n + 3 \cr}$$

(There are many ways to proceed from here. I decided to just use algebra, and to figure out what to do, I fiddled around on scratch paper! See if you can find another way to do this.)

The idea will be to rearrange the last expression into a sum of 4 terms, each of which I'll show is larger than the corresponding term in $n^3 + 6 n^2 + 12 n + 8$ . To do this, I'll break the $3 n^3$ term up into $n^3 + n^3 + n^3$ and rearrange the last two $n^3$ 's:

$$\eqalign{ 3^{n + 1} & > 3 n^3 + 9 n^2 + 9 n + 3 \cr & = n^3 + 9 n^2 + (n^3 + 9 n) + (n^3 + 3) \cr}$$

Now I compare this to $n^3 + 6 n^2 + 12 n + 8$ .

The first terms match: $n^3 = n^3$ .

For the second terms, I have $9 n^2 > 6 n^2$ .

For the third terms, I have to do a little work:

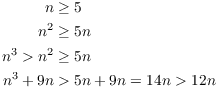
$$\eqalign{ n & \ge 5 \cr n^2 & \ge 5 n \cr n^3 > n^2 & \ge 5 n \cr n^3 + 9 n & > 5 n + 9 n = 14 n > 12 n \cr}$$

For the fourth terms, I do something similar:

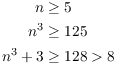
$$\eqalign{ n & \ge 5 \cr n^3 & \ge 125 \cr n^3 + 3 & \ge 128 > 8 \cr}$$

Adding up the equalities and inequalities, I have

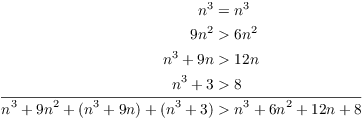
$$\eqalign{ n^3 & = n^3 \cr 9 n^2 & > 6 n^2 \cr n^3 + 9 n & > 12 n \cr n^3 + 3 & > 8 \cr \noalign{\vskip2pt \hrule \vskip2pt} n^3 + 9 n^2 + (n^3 + 9 n) + (n^3 + 3) & > n^3 + 6 n^2 + 12 n + 8 \cr}$$

Now I can wind up my proof:

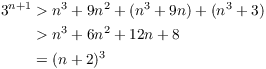
$$\eqalign{ 3^{n + 1} & > n^3 + 9 n^2 + (n^3 + 9 n) + (n^3 + 3) \cr & > n^3 + 6 n^2 + 12 n + 8 \cr & = (n + 2)^3 \cr}$$

This proves the result for $n + 1$ , so the result is true for $n > 5$ by induction.

I'll do the next example using general or strong induction --- that is, I'll assume the truth of all the statements preceding the $n^{\rm th}$ , rather than just the $(n - 1)^{\rm st}$ . Why? Because $a_n$ is defined in terms of $a_{n-1}$ and $a_{n-2}$ , rather than just $a_{n-1}$ , so I need to know that the induction hypothesis holds for $n - 2$ and $n - 1$ , not just $n - 1$ .

In addition, my basis step involves proving the result for $n = 0$ and for $n = 1$ , not just $n = 0$ . Why? Because the recursive definition for $a_n$ doesn't apply unless $n \ge 2$ .

Example. A sequence of integers is defined by

$$x_0 = 8, \quad x_1 = 14,$$

$$x_n = 2 x_{n - 1} + 8 x_{n - 2} \quad\hbox{for}\quad n \ge 2.$$

Prove that

$$x_n = 3 \cdot (-2)^n + 5 \cdot 4^n \quad\hbox{for}\quad n \ge 0.$$

Check the result for $n = 0$ :

$$a_0 = 8 \quad\hbox{and}\quad 3 \cdot (-2)^0 + 5 \cdot 4^0 = 8.$$

It works.

Check the result for $n = 1$ :

$$a_1 = 14 \quad\hbox{and}\quad 3 \cdot (-2)^1 + 5 \cdot 4^1 = 14.$$

It works.

Next, take $n \ge 2$ . Assume the result is true for all numbers less than n. In particular, the result is assumed true for $n - 1$ and $n - 2$ , so

$$x_{n - 1} = 3 \cdot (-2)^{n - 1} + 5 \cdot 4^{n - 1},$$

$$x_{n - 2} = 3 \cdot (-2)^{n - 2} + 5 \cdot 4^{n - 2}.$$

I want to prove the result for n, which is

$$x_n = 3 \cdot (-2)^n + 5 \cdot 4^n.$$

I have

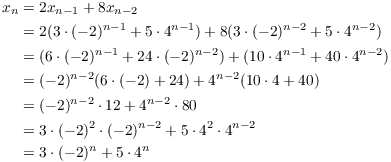
$$\eqalign{ x_n & = 2 x_{n - 1} + 8 x_{n - 2} \cr & = 2 (3 \cdot (-2)^{n - 1} + 5 \cdot 4^{n - 1}) + 8 (3 \cdot (-2)^{n - 2} + 5 \cdot 4^{n - 2}) \cr & = (6 \cdot (-2)^{n - 1} + 24 \cdot (-2)^{n - 2}) + (10 \cdot 4^{n - 1} + 40 \cdot 4^{n - 2}) \cr & = (-2)^{n - 2} (6 \cdot (-2) + 24) + 4^{n - 2} (10 \cdot 4 + 40) \cr & = (-2)^{n - 2} \cdot 12 + 4^{n - 2} \cdot 80 \cr & = 3 \cdot (-2)^2 \cdot (-2)^{n - 2} + 5 \cdot 4^2 \cdot 4^{n - 2} \cr & = 3 \cdot (-2)^n + 5 \cdot 4^n \cr}$$

The keys to the simplification are to group "like" terms together (the powers of 4 and the powers of -2 to get the second equality) and to make what you've got look like what you want (factoring out the powers of 4 and -2 to get the fourth equality).

This proves the statement for n, so the result is true for all n, by induction.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga