Linear Diophantine Equations

A Diophantine problem is one in which the solutions are required to be integers. Abusing terminology, I'll refer to Diophantine equations, meaning equations which are to be solved over the integers.

For example, the equation $x^3 + y^3 = z^3$ has many solutions over the reals. Here's a solution:

$$x = 1, \quad, y = 1, \quad z = {\root 3 \of 2}.$$

However, this equation has no nonzero integer solutions. This is a special case of Fermat's Last Theorem.

On the other hand, the following equation has infinitely many integer solutions:

$$9 x + 100 y = 1.$$

$(-11, 1)$ and $(89, -8)$ are examples of solutions.

In this section, I'll look at equations like the last one. They're called linear Diophantine equations.

Theorem. Let $a, b, c \in \integer$ . Consider the Diophantine equation

$$a x + b y = c.$$

(a) If $(a, b) \notdiv c$ , there are no solutions.

(b) If $(a, b) = d \mid c$ , there are infinitely many solutions of the form

$$x = x_0 + \dfrac{b}{d} t, \quad y = y_0 - \dfrac{a}{d} t.$$

Here $(x_0, y_0)$ is a particular solution, and $t \in \integer$ .

If you've had a course in differential equations, you may have seen something like this. $x = \dfrac{b}{d} t$ and $y = -\dfrac{a}{d} t$ give a general solution to the homogeneous equation

$$a x + b y = 0.$$

$(x_0, y_0)$ is a particular solution to $a x + b y = c$ . Their sum gives a general solution to the given (nonhomogeneous) equation.

Before I give the proof, I'll give some examples, and also discuss the three variable equation $a x + b y + c z = d$ .

Example. Solve $6 x + 9 y = 21$ .

Since $(6, 9) = 3 \mid 21$ , there are infinitely many solutions. Divide the equation by 3 to get

$$2 x + 3 y = 7.$$

By inspection, $x = 2$ and $y = 1$ is a particular solution. Hence, the general solution is

$$x = 2 + 3 t, \quad y = 1 - 2 t.$$

For example, setting $t = 5$ produces the solution $x = 17$ , $y = -9$ .

In general, you may not be able to see a particular solution by inspection. In that case, you can use the Extended Euclidean algorithm to generate one. We'll see how to do this in examples that follow.

Example. Solve $6 x + 9 y = 5$ .

Since $(6, 9) = 3 \notdiv 5$ , the equation has no solutions.

Example. Find all the solutions $(x, y)$ to the following Diophantine equation for which x and y are both positive.

$$11 x + 13 y = 369.$$

$(11, 13) = 1 \mid 369$ , so there are solutions.

It is too hard to guess a particular solution, so I'll use the Extended Euclidean algorithm:

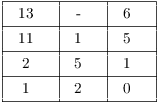
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 13 & & - & & 6 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 11 & & 1 & & 5 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 5 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 11 \cdot 6 + 13 \cdot (-5) & = 1 \cr 11 \cdot 2214 + 13 \cdot (-1845) & = 369 \cr}$$

Matching this with the given equation $11 x + 13 y = 369$ , I see that $(x, y) = (2214, -1845)$ is a particular solution. The general solution is

$$x = 2214 + 13 t, \quad y = -1845 - 11 t.$$

I want solutions for which x and y are both positive. So

$$2214 + 13 t > 0, \quad\hbox{so}\quad t > -\dfrac{2214}{13} = -170.30769 \ldots.$$

$$-1845 - 11 t > 0, \quad\hbox{so}\quad t < -\dfrac{1845}{11} = -167.72727 \ldots.$$

The integers which satisfy both of these inequalities are $t = -170, -169, -168$ . Here are the values of x and y:

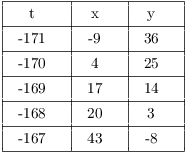
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & t & & x & & y & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & -171 & & -9 & & 36 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & -170 & & 4 & & 25 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & -169 & & 17 & & 14 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & -168 & & 20 & & 3 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & -167 & & 43 & & -8 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The solutions are $(x, y) = (4, 25)$ , $(17, 14)$ , and $(20, 3)$ .

The requirement that the solutions be positive can come up in real-world problems.

Example. Phoebe buys large shirts for $18 each and small shirts for $11 each. The shirts cost a total of $1188. What is the smallest total number of shirts she could have bought?

Let x be the number of large shirts and let y be the number of small shirts. Then

$$18 x + 11 y = 1188.$$

Since $(18, 11) = 1 \mid 1188$ , there are solutions.

I'll use the Extended Euclidean algorithm to get a particular solution:

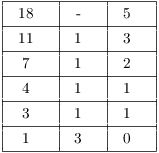
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 18 & & - & & 5 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 11 & & 1 & & 3 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 7 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ 18 \cdot (-3) + 11 \cdot 5 & = 1 \cr 18 \cdot (-3564) + 11 \cdot 5940 & = 1188 \cr}$$

$x = -3564$ and $y = 5940$ is a particular solution. The general solution is

$$x = -3564 + 11 t, \quad y = 5940 - 18 t.$$

Since the number of shirts can't be negative, I have $x \ge 0$ and $y \ge 0$ .

$$x \ge 0 \quad\hbox{gives}\quad -3564 + 11 t \ge 0 \quad\hbox{so}\quad t \ge \dfrac{3564}{11} = 324.$$

$$y \ge 0 \quad\hbox{gives}\quad 5940 - 18 t \ge 0 \quad\hbox{so}\quad t \le \dfrac{5940}{18} = 330.$$

Thus, $324 \le t \le 330$ .

The total number of shirts is

$$x + y = (-3564 + 11 t) + (5940 - 18 t) = 2376 - 7 t.$$

For $324 \le t \le 330$ , this is smallest for $t = 330$ , which gives

$$x = 66, \quad y = 0, \quad x + y = 66.$$

She bought 66 large shirts, no small shirts, and a total of 66 shirts.

Consider a 3-variable equation

$$a x + b y + c z = d.$$

The equation has solutions if and only if $(a, b, c) \mid d$ . If it has solutions, there will be infinitely many, determined by two integer parameters.

You can solve a 3-variable equation by reducing it to a 2-variable equation. Group the first two terms and factor out the greatest common divisor of their coefficients. Introduce a new variable, defining it to be what is left after the greatest common divisor is factored out. The new equation is a 2-variable Diophantine equation, which you can solve using the method described earlier.

Example. Find the general solution to the following Diophantine equation.

$$8 x + 14 y + 5 z = 11.$$

$$2(4 x + 7 y) + 5 z = 11.$$

Let $w = 4 x + 7 y$ .

$$2 w + 5 z = 11.$$

$w = -22$ and $z = 11$ is a particular solution. So

$$w = -22 + 5 s \quad\hbox{and}\quad z = 11 - 2 s.$$

Then

$$4 x + 7 y = w = -22 + 5 s.$$

$x = -44 + 10 s$ and $y = 22 - 5 s$ is a particular solution. The general solution is

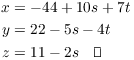
$$\eqalign{ x & = -44 + 10 s + 7 t \cr y & = 22 - 5 s - 4 t \cr z & = 11 - 2 s \quad\halmos \cr}$$

A general linear Diophantine equation has the form

$$a_1 x_1 + \cdots a_nx_n = c.$$

There are solutions if $(a_1, \ldots a_n) \mid c$ . If there is a solution, it will in general have $n - 1$ parameters --- exactly as you'd expect from linear algebra.

Here's the proof of the theorem for the two-variable case.

Proof. (two variable case) Consider the linear Diophantine equation

$$a x + b y = c.$$

Case 1. Suppose $(a, b) \notdiv c$ . If x and y are solutions to the equation, then

$$(a, b) \mid a x + b y = c.$$

This contradiction shows that there cannot be a solution.

Case 2. Suppose $(a, b) \mid c$ . Write $c = k (a, b)$ for $k \in \integer$ . There are integers m and n such that

$$a m + b n = (a, b).$$

Then

$$a m k + b n k = (a, b) k = c.$$

Hence, $x = k m$ , $y = k n$ , is a solution.

Suppose $x = x_0$ , $y = y_0$ , is a particular solution. Then

$$a \left(x_0 + \dfrac{b}{d} t\right) + b \left(y_0 - \dfrac{a}{d} t\right) = \dfrac{a b}{d} t - \dfrac{a b}{d} t + (a x_0 + b y_0) = 0 + c = c.$$

This proves that $x = x_0 + \dfrac{b}{d} t$ , $y = y_0 - \dfrac{a}{d} t$ is a solution for every $t \in \integer$ .

Finally, I want to show that every solution has this form. Suppose then that $(x, y)$ is a solution. Then $a x + b y = c$ and $a x_0 + b y_0 = c$ imply

$$a(x - x_0) + b(y - y_0) = c - c = 0.$$

Therefore,

$$\dfrac{a}{(a, b)}(x - x_0) + \dfrac{b}{(a, b)}(y - y_0) = 0,$$

$$\dfrac{b}{(a, b)}(y - y_0) = -\dfrac{a}{(a, b)}(x - x_0).$$

Now $\dfrac{b}{(a, b)}$ divides the left side, so it divides the right side. However, $\left(\dfrac{a}{(a, b)},\dfrac{b}{(a, b)}\right) = 1$ . Therefore,

$$\dfrac{b}{(a, b)} \bigm| x - x_0, \quad\hbox{or}\quad x - x_0 = t \cdot \dfrac{b}{(a, b)} \quad\hbox{for some}\quad t \in \integer.$$

Thus,

$$x = x_0 + t \cdot \dfrac{b}{(a, b)}.$$

Substitute $x - x_0 = t \cdot \dfrac{b}{(a, b)}$ back into the last x-y equation above:

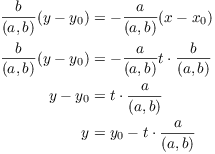
$$\eqalign{ \dfrac{b}{(a, b)}(y - y_0) & = -\dfrac{a}{(a, b)}(x - x_0) \cr \dfrac{b}{(a, b)}(y - y_0) & = -\dfrac{a}{(a, b)} t \cdot \dfrac{b}{(a, b)} \cr y - y_0 & = t \cdot \dfrac{a}{(a, b)} \cr y & = y_0 - t \cdot \dfrac{a}{(a, b)} \cr}$$

Thus,

$$x = x_0 + t \cdot \dfrac{b}{(a, b)} \quad\hbox{and}\quad y = y_0 - t \cdot \dfrac{a}{(a, b)}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga