Systems of Congruences

Systems of linear congruences can be solved using methods from linear algebra: Matrix inversion, Cramer's rule, or row reduction. In case the modulus is prime, everything you know from linear algebra goes over to systems of linear congruences. (The reason is the $\integer_p$ is a field, for p prime, and linear algebra works fine over any field --- not just $\real$ and $\complex$ .)

It's also possible to convert a system to a linear Diophantine equation.

I will stick to prime moduli for simplicity. I'll assume that you know some linear algebra, even if you haven't seen it done with modular arithmetic.

In the first example, I'll use the well-known fact that a matrix is invertible if and only if its determinant is nonzero.

Example. Solve

$\eqalign{ 2 x + 6 y & = 1 \mod{7} \cr 4 x + 3 y & = 2 \mod{7} \cr}$

Write the system in matrix form:

$\left[\matrix{2 & 6 \cr 4 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{1 \cr 2 \cr}\right].$

The determinant of the coefficient matrix is $2\cdot 3 - 4\cdot 6 = -18 = 3 \mod{7}$ . In particular, it's nonzero mod 7, so the system has a solution. For a $2 \times 2$ system, it's easiest to use the formula for inverting a $2 \times 2$ matrix:

$\left[\matrix{a & b \cr c & d \cr}\right]^{-1} = (a d - b c)^{-1} \left[\matrix{d & -b \cr -c & a \cr}\right].$

If I apply this formula to the coefficient matrix for the system, I get

$\left[\matrix{2 & 6 \cr 4 & 3 \cr}\right]^{-1} = (2 \cdot 3 - 4 \cdot 6)^{-1} \left[\matrix{3 & -6 \cr -4 & 2 \cr}\right] = (-18)^{-1} \left[\matrix{3 & 1 \cr 3 & 2 \cr}\right] = 3^{-1} \left[\matrix{3 & 1 \cr 3 & 2 \cr}\right] = 5 \cdot \left[\matrix{3 & 1 \cr 3 & 2 \cr}\right].$

The inverse of 3 mod 7 is 5, since $3 \cdot 5 = 1 \mod{7}$ .

All I have to do is multiply both sides of the equation on the left by the inverse of the coefficient matrix:

$\left[\matrix{2 & 6 \cr 4 & 3 \cr}\right]^{-1} \left[\matrix{2 & 6 \cr 4 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{2 & 6 \cr 4 & 3 \cr}\right]^{-1} \left[\matrix{1 \cr 2 \cr}\right],$

$\left[\matrix{x \cr y \cr}\right] = 5 \cdot \left[\matrix{3 & 1 \cr 3 & 2 \cr}\right] \left[\matrix{1 \cr 2 \cr}\right] = 5 \cdot \left[\matrix{5 \cr 0 \cr}\right] = \left[\matrix{4 \cr 0 \cr}\right].$

The solution is

$x = 4 \mod{7}, \quad y = 0 \mod{7}.$

You can also solve this equation using Cramer's rule, or by row reduction. You can even use basic algebra, though it's a little tedious. Solve the first equation for one of the variables:

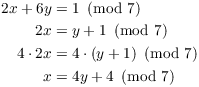
$\eqalign{ 2 x + 6 y & = 1 \mod{7} \cr 2 x & = y + 1 \mod{7} \cr 4 \cdot 2 x & = 4 \cdot (y + 1) \mod{7} \cr x & = 4 y + 4 \mod{7} \cr}$

Substitute this into the second equation:

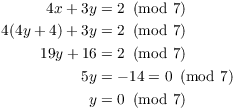
$\eqalign{ 4 x + 3 y & = 2 \mod{7} \cr 4 (4 y + 4) + 3 y & = 2 \mod{7} \cr 19 y + 16 & = 2 \mod{7} \cr 5 y & = -14 = 0 \mod{7} \cr y & = 0 \mod{7} \cr}$

Plugging this back into the x-equation gives $x = 4 \cdot 0 + 4 = 4 \mod{7}$ .

In some cases, you can convert a system to a linear Diophantine equation, which we already know how to solve.

Example. Solve the following system over $\integer_7$ :

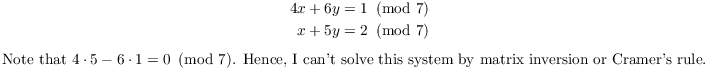
$$$\eqalign{ 4 x + 6 y & = 1 \mod{7} \cr x + 5 y & = 2 \mod{7} \cr}$$ Note that $4 \cdot 5 - 6 \cdot 1 = 0 \mod{7}$. Hence, I can't solve this system by matrix inversion or Cramer's rule.$

Note, however, that the first equation is 4 times the second:

$4(x + 5 y) = 4 x + 6 y, \quad 4 \cdot 2 = 1.$

So it suffices to solve

$x + 5 y = 2 \mod{7}.$

This is equivalent to the Diophantine equation

Let . This gives

The general solution is

$w = 2 + 7 t, \quad z = 0 - t.$

z is just a helper variable, so ignore it. Using the w-equation, I have

The general solution is

$x = 2 + 7 t + 5 s, \quad y = -s.$

Recall that the original system was mod 7:

$x = 2 + 5 s \mod{7}, \quad y = 6 s \mod{7}.$

Note that this is a parametrized solution. You could also do this problem by row reduction.

Example. Solve

$\eqalign{ 4 x + 6 y & = 3 \mod{7} \cr x + 5 y & = 2 \mod{7} \cr}$

As before, multiplying the second equation by 4 gives

$4 x + 6 y = 1 \mod{7}.$

But the two equations now imply " $3 = 1 \mod{7}$ ", and this contradiction implies that the system has no solutions.

Example. Solve

$\matrix{ x & + & 2 y & & & = & 4 & \mod{5}\cr 3 x & + & y & + & z & = & 0 & \mod{5}\cr x & + & y & + & 2 z & = & 3 & \mod{5}\cr}$

With a system this large, it's better to use row reduction.

$\left[\matrix{ 1 & 2 & 0 & 4 \cr 3 & 1 & 1 & 0 \cr 1 & 1 & 2 & 3 \cr}\right] \matrix{\longrightarrow \cr r_2 \to r_2 + 2r_1 \cr} \left[\matrix{ 1 & 2 & 0 & 4 \cr 0 & 0 & 1 & 3 \cr 1 & 1 & 2 & 3 \cr}\right] \matrix{\longrightarrow \cr r_3 \to r_3 + 4r_1 \cr} \left[\matrix{ 1 & 2 & 0 & 4 \cr 0 & 0 & 1 & 3 \cr 0 & 4 & 2 & 4 \cr}\right] \matrix{\longrightarrow \cr r_2 \leftrightarrow r_3 \cr} \left[\matrix{ 1 & 2 & 0 & 4 \cr 0 & 4 & 2 & 4 \cr 0 & 0 & 1 & 3 \cr}\right]$

$\matrix{\longrightarrow \cr r_2 \to 4r_2 \cr} \left[\matrix{ 1 & 2 & 0 & 4 \cr 0 & 1 & 3 & 1 \cr 0 & 0 & 1 & 3 \cr}\right] \matrix{\longrightarrow \cr r_1 \to r_1 + 3r_2 \cr} \left[\matrix{ 1 & 0 & 4 & 2 \cr 0 & 1 & 3 & 1 \cr 0 & 0 & 1 & 3 \cr}\right] \matrix{\longrightarrow \cr r_1 \to r_1 + r_3 \cr}$

$\left[\matrix{ 1 & 0 & 0 & 0 \cr 0 & 1 & 3 & 1 \cr 0 & 0 & 1 & 3 \cr}\right] \matrix{\longrightarrow \cr r_2 \to r_2 + 2r_3 \cr} \left[\matrix{ 1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 2 \cr 0 & 0 & 1 & 3 \cr}\right]$

The solution is

$x = 0 \mod{5}, \quad y = 2 \mod{5}, \quad z = 3 \mod{5}.\quad\halmos$

Example. Solve

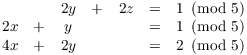
$\matrix{ & & 2 y & + & 2 z & = & 1 \mod{5} \cr 2 x & + & y & & & = & 1 \mod{5} \cr 4 x & + & 2 y & & & = & 2 \mod{5} \cr}$

I'll do this by row reduction:

$\left[\matrix{ 0 & 2 & 2 & 1 \cr 2 & 1 & 0 & 1 \cr 4 & 2 & 0 & 2 \cr}\right] \matrix{\longrightarrow \cr r_1 \leftrightarrow r_3 \cr} \left[\matrix{ 4 & 2 & 0 & 2 \cr 2 & 1 & 0 & 1 \cr 0 & 2 & 2 & 1 \cr}\right] \matrix{\longrightarrow \cr r_1 \to 4r_1 \cr} \left[\matrix{ 1 & 3 & 0 & 3 \cr 2 & 1 & 0 & 1 \cr 0 & 2 & 2 & 1 \cr}\right] \matrix{\longrightarrow \cr r_2 \to r_2+3r_1 \cr} \left[\matrix{ 1 & 3 & 0 & 3 \cr 0 & 0 & 0 & 0 \cr 0 & 2 & 2 & 1 \cr}\right] \matrix{\longrightarrow \cr r_2 \leftrightarrow r_3 \cr}$

$\left[\matrix{ 1 & 3 & 0 & 3 \cr 0 & 2 & 2 & 1 \cr 0 & 0 & 0 & 0 \cr}\right] \matrix{\longrightarrow \cr r_2 \to 3r_2 \cr} \left[\matrix{ 1 & 3 & 0 & 3 \cr 0 & 1 & 1 & 3 \cr 0 & 0 & 0 & 0 \cr}\right] \matrix{\longrightarrow \cr r_1 \to r_1+2r_2 \cr} \left[\matrix{ 1 & 0 & 2 & 4 \cr 0 & 1 & 1 & 3 \cr 0 & 0 & 0 & 0 \cr}\right]$

The equations are

$x + 2 z = 4 \mod{5}, \quad y + z = 3 \mod{5}.$

There are multiple solutions --- in fact, since there is one free variable (z), there will be 5 distinct solutions mod 5. As is customary when a system has multiple solutions, I'll write the solution in parametric form.

Set . Then , so (by adding to both sides). Likewise, , so . The solution is

$x = 3 t + 4 \mod{5}, \quad y = 4 t + 3 \mod{5}, \quad z = t \mod{5}.\quad\halmos$

As noted above, it's possible to do a lot of linear algebra mod n. Here's an example.

Example. Compute the inverse mod 3 of the matrix

$$$A = \left[\matrix{ 1 & 2 & 0 \cr 0 & 1 & 1 \cr 1 & 0 & 2 \cr}\right].$$ Recall the algorithm for inverting a matrix by row-reduction: Put a copy of the $3 \times 3$ identity matrix on the right of the original matrix, then row reduce the resulting $3 \times 6$ matrix. When the block on the left becomes the identity, the block on the right will have turned into $A^{-1}$.$

$\left[\matrix{ 1 & 2 & 0 & 1 & 0 & 0 \cr 0 & 1 & 1 & 0 & 1 & 0 \cr 1 & 0 & 2 & 0 & 0 & 1 \cr}\right] \matrix{\longrightarrow \cr r_3 \to r_3 + 2r_1 \cr} \left[\matrix{ 1 & 2 & 0 & 1 & 0 & 0 \cr 0 & 1 & 1 & 0 & 1 & 0 \cr 0 & 1 & 2 & 2 & 0 & 1 \cr}\right] \matrix{\longrightarrow \cr r_1 \to r_1 + r_2 \cr}$

$\left[\matrix{ 1 & 0 & 1 & 1 & 1 & 0 \cr 0 & 1 & 1 & 0 & 1 & 0 \cr 0 & 1 & 2 & 2 & 0 & 1 \cr}\right] \matrix{\longrightarrow \cr r_3 \to r_3 + 2r_2 \cr} \left[\matrix{ 1 & 0 & 1 & 1 & 1 & 0 \cr 0 & 1 & 1 & 0 & 1 & 0 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right] \matrix{\longrightarrow \cr r_1 \to r_1 + 2r_3 \cr}$

$\left[\matrix{ 1 & 0 & 0 & 2 & 2 & 2 \cr 0 & 1 & 1 & 0 & 1 & 0 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right] \matrix{\longrightarrow \cr r_2 \to r_2 + 2r_3 \cr} \left[\matrix{ 1 & 0 & 0 & 2 & 2 & 2 \cr 0 & 1 & 0 & 1 & 2 & 2 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right]$

Thus,

$A^{-1} = \left[\matrix{ 2 & 2 & 2 \cr 1 & 2 & 2 \cr 2 & 2 & 1 \cr}\right].\quad\halmos$

Example. Is the following matrix invertible mod 6?

$\left[\matrix{5 & 1 \cr 3 & 1 \cr}\right]$

When the modulus is not prime, results from linear algebra must be used with care. In this case, I'd like to use the determinant to tell whether the matrix is invertible.

$\det \left[\matrix{5 & 1 \cr 3 & 1 \cr}\right] = 5 - 3 = 2.$

Normally, a nonzero determinant means that the matrix is invertible. However, mod n the criterion is that the determinant must be relatively prime to n. Since $(2, 6) = 2 \ne 1$ , the matrix is not invertible. So, for instance, if you try apply the standard matrix inversion algorithm to find the inverse, you'll find that it won't work.

Contact information

Bruce Ikenaga's Home Page