Review Sheet for Test 2

Math 311

These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence of a topic does not imply that it won't appear on the test.

1. Find the domain of the function $f(x, y) = \dfrac{x^2 + y^2}{(x - 1)(y - 3)}$ .

2. Find the domain and range of $f(x, y, z) = \dfrac{z^2 + 1}{\sqrt{1 - x^2 - y^2}}$ .

3. Compute $\displaystyle \lim_{(x, y)\to (2, 1)} \dfrac{3 x + 2 y + 51}{x^2 + 3 y^2}$ .

4. Show that $\displaystyle \lim_{(x, y)\to (0, 0)} \dfrac{3 x^4 + 5 y^4}{x^4 + 3 x^2 y^2 + y^4}$ is undefined.

5. Compute $\displaystyle \lim_{(x, y) \to (0, 0)} \dfrac{(x^2 + y^2)^{3/2}}{x^2 + y^2 + 1}$ by converting to polar coordinates.

6. Show that $\displaystyle \lim_{(x, y)\to (0, 0)} \dfrac{x^4 y^4}{x^4 + 3 x^2 y^2 + y^4}$ is defined and find its value.

7. Define $f: \real^2 \to \real$ by

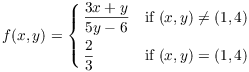
$$f(x, y) = \cases{ \dfrac{3 x + y}{5 y - 6} & if $(x, y) \ne (1, 4)$ \cr \noalign{\vskip2pt} \dfrac{2}{3} & if $(x, y) = (1, 4)$ \cr}$$

Determine whether f is continuous at $(1, 4)$ .

8. Compute the following partial derivatives:

(a) $\pder {} x x^2 \sin (x^3 + 5 y)$ and $\pder {} y x^2 \sin (x^3 + 5 y)$ .

(b) $\pder {} s \dfrac{s^2}{s^3 + t^3}$ and $\pder {} t \dfrac{s^2}{s^3 + t^3}$ .

(c) $\dfrac{\partial^3 f}{\partial x^2 \partial y}$ , if

$$f(x, y) = e^{3 x} + 4 x^2 y - \ln y.$$

(d) $\dfrac{\partial^3 f}{\partial x \partial y \partial z}$ , if

$$f(x, y, z) = 3 x + 8 y - 2 z + x^2 y^3 z^4.$$

9. Let

$$f(x, y) = x^3 + 5 x y^2 - y^4.$$

Construct the Taylor series for f at the point $(2, 1)$ , writing terms through the $2^{\rm nd}$ order.

10. For a differentiable function $f(x, y)$ ,

$$f(-2, 4) = 6, \quad f_x(-2, 4) = 3, \quad f_y(-2, 4) = 1.$$

Use a $1^{\rm st}$ -degree Taylor approximation at $(-2, 4)$ to approximate $f(-2.1, 4.1)$ .

11. Find the tangent plane and the normal line to the surface

$$z = x (2 x + y)^3 \quad\hbox{at}\quad (x, y) = (2, -3).$$

12. Find the tangent plane to the surface

$$x = u^2 - 3 v^2, \quad y = \dfrac{4 u}{v}, \quad z = 2 u^2 v^3 \quad\hbox{at}\quad (u, v) = (1, 1).$$

13. Use a linear approximation to $z = f(x, y) = x^2 - y^2$ at the point $(2, 1)$ to approximate $f(1.9, 1.1)$ .

14. Let $f(x, y) = \dfrac{(x + 4)^2}{y}$ .

(a) Find a unit vector at $(-3, 1)$ which points in the direction of most rapid increase.

(b) Find the rate of most rapid increase at $(-3, 1)$ .

15. Find the gradient of $f(x, y, z) = \dfrac{1}{\sqrt{x^2 + y^2 + z^2 + 1}}$ and show that it always points toward the origin.

16. Let $f(x, y) = \sqrt{x^2 + 2 y + 3}$ . Find the directional derivative of f at the point $(3, 2)$ in the direction of the vector $(-4, 3)$ .

17. Find the rate of change of $f(x, y, z) = x y - y z + x z$ at the point $(1, -2, -2)$ in the direction toward the origin. Is f increasing or decreasing in this direction?

18. The rate of change of $f(x, y)$ at $(1, -1)$ is 2 in the direction toward $(5, -1)$ and is $\dfrac{6}{5}$ in the direction of the vector $(-3, -4)$ . Find $\nabla f(1, -1)$ .

19. Calvin Butterball sits in his go-cart on the surface

$$z = x^3 - 2 x^2 y + x^2 + x y^2 - 2 y^3 + y^2 \quad\hbox{at the point}\quad (1, 1, 0).$$

If his go-cart is pointed in the direction of the vector $\vec v = (15, -8)$ , at what rate will it roll downhill?

20. Find the tangent plane to $x^2 - y^2 + 2 y z + z^5 = 6$ at the point $(2, 1, 1)$ .

21. Suppose that $z = f(x, y)$ and $(x, y) = g(u, v)$ are given by

$$z = x^4 + 3 x y^2 - y^2, \quad (x, y) = (\sin 5 u + \cos v, \cos 3 u + \sin 2 v).$$

Find $\pder z u$ and $\pder z v$ .

22. Let r and $\theta$ be the standard polar coordinates variables. Use the Chain Rule to find $\pder f r$ and $\pder f \theta$ , for $f(x, y) = x e^x + e^y$ .

23. Suppose $u = f(x, y, z)$ and $x = \phi(s, t)$ , $y = \psi(s, t)$ , $z = \mu(s, t)$ . Use the Chain Rule to write down an expression for $\pder u t$ .

24. Suppose that $w = f(x, y)$ , $x = g(r, s, t)$ , and $y = h(r, t, s)$ . Use the Chain Rule to find an expression for $\pdertwo f t$ .

25. Locate and classify the critical points of

$$z = x^2 y - 4 xy + \dfrac{1}{3}y^3 - \dfrac{3}{2}y^2.$$

26. Locate and classify the critical points of

$$f(x, y) = 6 x y^2 - 2 x^3 y + y^2.$$

27. Find the critical points of

$$z = (x^2 + y^2) e^{-x^2 - 4 y^2}.$$

You do not need to classify them.

28. Find the points on the sphere $x^2 + y^2 + z^2 = 36$ which are closest to and farthest from the point $(4, -3, 12)$ .

29. A rectangular box (with a bottom and a top) is to have a total surface area of $6 c^2$ , where $c > 0$ . Show that the box of largest volume satisfying this condition is a cube with sides of length c.

30. (a) Find the critical points of

$$w = 4 x y z \quad\hbox{subject to the constraint}\quad x + y + z = 3.$$

(b) Express w as a function of x and y by eliminating z, then consider the behavior of w for $x = y$ . Explain why the critical points in (a) can't give absolute maxes or mins.

31. Find the largest and smallest values of $f(x,y) = 4 x^2 y$ subject to the constraint $x^2 + y^2 = 36$ .

Solutions to the Review Sheet for Test 2

1. Find the domain of the function $f(x, y) = \dfrac{x^2 + y^2}{(x - 1)(y - 3)}$ .

Since the denominator of the fraction can't be 0, the domain is

$$\{(x, y) \mid x \ne 1 \quad\hbox{and}\quad y \ne 3\}.$$

It consists of all points except those lying on the lines $x = 1$ or $y = 3$ .

2. Find the domain and range of $f(x, y, z) = \dfrac{z^2 + 1}{\sqrt{1 - x^2 - y^2}}$ .

Since the expression inside the square root must be positive, the function is defined for $1 - x^2 - y^2 > 0$ . Therefore, the domain is the set of points $(x, y, z)$ such that $x^2 + y^2 < 1$ --- that is, the interior of the cylinder $x^2 + y^2 = 1$ of radius 1 whose axis is the z-axis. (There are no restrictions on z.)

To find the range, note that $z^2 + 1 \ge 1$ . Also,

$$1 - x^2 - y^2 \le 1, \quad\hbox{and}\quad \sqrt{1 - x^2 - y^2} \le 1, \quad\hbox{so}\quad \dfrac{1}{\sqrt{1 - x^2 - y^2}} \ge 1.$$

Hence,

$$f(x, y, z) = \dfrac{z^2 + 1}{\sqrt{1 - x^2 - y^2}} \ge 1 \cdot 1 = 1.$$

This shows that every output of f is greater than or equal to 1.

On the other hand, suppose $k \ge 1$ . Then

$$f(0, 0, \sqrt{k - 1}) = \dfrac{(\sqrt{k - 1})^2 + 1}{\sqrt{1 - 0 - 0}} = k.$$

This shows that every number greater than or equal to 1 is an output of f.

Hence, the range of f is the set of numbers w such that $w \ge 1$ .

3. Compute $\displaystyle \lim_{(x, y)\to (2, 1)} \dfrac{3 x + 2 y + 51}{x^2 + 3 y^2}$ .

$$\lim_{(x, y)\to (2, 1)} \dfrac{3 x + 2 y + 5}{x^2 + 3 y^2} = \dfrac{6 + 2 + 5}{4 + 3} = \dfrac{13}{7}.\quad\halmos$$

4. Show that $\displaystyle \lim_{(x, y)\to (0, 0)} \dfrac{3 x^4 + 5 y^4}{x^4 + 3 x^2 y^2 + y^4}$ is undefined.

If you approach $(0, 0)$ along the x-axis ($y = 0$ ), you get

$$\lim_{(x, y)\to (0, 0)} \dfrac{3 x^4 + 5 y^4}{x^4 + 3 x^2 y^2 + y^4} = \lim_{(x, y)\to (0, 0)} \dfrac{3 x^4}{x^4} = \lim_{(x, y)\to (0, 0)} 3 = 3.$$

If you approach $(0, 0)$ along the line $y = x$ , you get

$$\lim_{(x, y)\to (0, 0)} \dfrac{3 x^4 + 5 y^4}{x^4 + 3 x^2 y^2 + y^4} = \lim_{(x, y)\to (0, 0)} \dfrac{3 x^4 + 5 x^4}{x^4 + 3 x^4 + x^4} = \lim_{(x, y)\to (0, 0)} \dfrac{8 x^4}{5 x^4} = \lim_{(x, y)\to (0, 0)} \dfrac{8}{5} = \dfrac{8}{5}.$$

Since the function approaches different values as you approach $(0, 0)$ in different ways, the limit is undefined.

5. Compute $\displaystyle \lim_{(x, y) \to (0, 0)} \dfrac{(x^2 + y^2)^{3/2}}{x^2 + y^2 + 1}$ by converting to polar coordinates.

Set $r^2 = x^2 + y^2$ . As $(x, y) \to (0, 0)$ , I have $r \to 0$ . So

$$\lim_{(x, y) \to (0, 0)} \dfrac{(x^2 + y^2)^{3/2}}{x^2 + y^2 + 1} = \lim_{r \to 0} \dfrac{(r^2)^{3/2}}{r^2 + 1} = \lim_{r \to 0} \dfrac{r^3}{r^2 + 1} = \dfrac{0}{0 + 1} = 0.\quad\halmos$$

6. Show that $\displaystyle \lim_{(x, y)\to (0, 0)} \dfrac{x^4 y^4}{x^4 + 3 x^2 y^2 + y^4}$ is defined and find its value.

$$\left|\dfrac{x^4 y^4}{x^4 + 3 x^2 y^2 + y^4}\right| \le \left|\dfrac{x^4 y^4}{x^4}\right| = |y^4| \to 0 \quad\hbox{as}\quad (x, y)\to (0, 0).$$

Therefore,

$$\lim_{(x, y)\to (0, 0)} \left|\dfrac{x^4 y^4}{x^4 + 3 x^2 y^2 + y^4}\right| = 0.$$

Hence,

$$\lim_{(x, y)\to (0, 0)} \dfrac{x^4 y^4}{x^4 + 3 x^2 y^2 + y^4} = 0.\quad\halmos$$

7. Define $f: \real^2 \to \real$ by

$$f(x, y) = \cases{ \dfrac{3 x + y}{5 y - 6} & if $(x, y) \ne (1, 4)$ \cr \noalign{\vskip2pt} \dfrac{2}{3} & if $(x, y) = (1, 4)$ \cr}$$

Determine whether f is continuous at $(1, 4)$ .

$$\lim_{(x, y) \to (1, 4)} f(x, y) = \lim_{(x, y) \to (1, 4)} \dfrac{3 x + y}{5 y - 6} = \dfrac{3 + 4}{20 - 6} = \dfrac{1}{2}.$$

Since $f(1, 4) = \dfrac{1}{2}$ ,

$$\lim_{(x, y) \to (1, 4)} f(x, y) \ne f(1, 4).$$

Therefore, f is not continuous at $(1, 4)$ .

8. Compute the following partial derivatives:

(a) $\pder {} x x^2 \sin (x^3 + 5 y)$ and $\pder {} y x^2 \sin (x^3 + 5 y)$ .

(b) $\pder {} s \dfrac{s^2}{s^3 + t^3}$ and $\pder {} t \dfrac{s^2}{s^3 + t^3}$ .

(c) $\dfrac{\partial^3 f}{\partial x^2 \partial y}$ , if

$$f(x, y) = e^{3 x} + 4 x^2 y - \ln y.$$

(d) $\dfrac{\partial^3 f}{\partial x \partial y \partial z}$ , if

$$f(x, y, z) = 3 x + 8 y - 2 z + x^2 y^3 z^4.$$

(a)

$$\pder {} x x^2 \sin (x^3 + 5 y) = 3 x^4 \cos (x^3 + 5 y) + 2 x \sin (x^3 + 5 y).$$

$$\pder {} y x^2 \sin (x^3 + 5 y) = 5 x^2 \cos (x^3 + 5 y).\quad\halmos$$

(b)

$$\pder {} s \dfrac{s^2}{s^3 + t^3} = \dfrac{(s^3 + t^3)(2 s) - (s^2)(3 s^2)}{(s^3 + t^3)^2}.$$

$$\pder {} t \dfrac{s^2}{s^3 + t^3} = -\dfrac{3 s^2 t^2}{(s^3 + t^3)^2}.\quad\halmos$$

(c)

$$\pder f y = 4 x^2 - \dfrac{1}{y}.$$

$$\pdertwom f x y = 8 x.$$

$$\dfrac{\partial^3 f}{\partial x^2 \partial y} = 8.\quad\halmos$$

(d)

$$\pder f z = -2 + 4 x^2 y^3 z^3.$$

$$\pdertwom f y z = 12 x^2 y^2 z^3.$$

$$\dfrac{\partial^3 f}{\partial x \partial y \partial z} = 24 x y^2 z^3.\quad\halmos$$

9. Let

$$f(x, y) = x^3 + 5 x y^2 - y^4.$$

Construct the Taylor series for f at the point $(2, 1)$ , writing terms through the $2^{\rm nd}$ order.

$$\pder f x = 3 x^2 + 5 y^2, \quad \pder f y = 10 x y - 4 y^3.$$

$$\pdertwo f x = 6 x, \quad \pdertwom f x y = 10 y, \quad \pdertwo f y = 10 x - 12 y^2.$$

At $(2, 1)$ ,

$$f(2, 1) = 17, \quad \pder f x (2, 1) = 17, \quad \pder f y (2, 1) = 16.$$

$$\pdertwo f x (2, 1) = 12, \quad \pdertwom f x y (2, 1) = 10, \quad \pdertwo f y (2, 1) = 8.$$

The series is

$$f(x, y) = 17 + \left(17 (x - 2) + 16 (y - 1)\right) + \dfrac{1}{2!} \left(12 (x - 2)^2 + 20 (x - 2)(y - 1) + 8 (y - 1)^2\right) + \cdots.\quad\halmos$$

10. For a differentiable function $f(x, y)$ ,

$$f(-2, 4) = 6, \quad f_x(-2, 4) = 3, \quad f_y(-2, 4) = 1.$$

Use a $1^{\rm st}$ -degree Taylor approximation at $(-2, 4)$ to approximate $f(-2.1, 4.1)$ .

The $1^{\rm st}$ -degree Taylor approximation is

$$f(x, y) \approx 6 + \left(3 (x + 2) + (y - 4)\right).$$

Hence,

$$f(-2.1, 4.1) \approx 6 + 3 (-0.1) + 0.1 = 5.8.\quad\halmos$$

11. Find the tangent plane and the normal line to the surface

$$z = x (2 x + y)^3 \quad\hbox{at}\quad (x, y) = (2, -3).$$

When $(x, y) = (2, -3)$ ,

$$z = 2 \cdot 1^3 = 2.$$

The point of tangency is $(2, -3, 2)$ .

$$\pder f x = 6 x (2 x + y)^2 + (2 x + y)^3, \quad \pder f x (2, -3) = 13.$$

$$\pder f y = 3 x (2 x + y)^2, \quad \pder f y (2, -3) = 6.$$

The normal vector is

$$\left(-\pder f x, -\pder f y, 1\right) = (-13, -6, 1).$$

The normal line is

$$x - 2 = -13 t, \quad y + 3 = -6 t, \quad z - 2 = t.$$

The tangent plane is

$$-13 (x - 2) - 6 (y + 3) + (z - 2) = 0, \quad\hbox{or}\quad -13 x - 6 y + z = -6.\quad\halmos$$

12. Find the tangent plane to the surface

$$x = u^2 - 3 v^2, \quad y = \dfrac{4 u}{v}, \quad z = 2 u^2 v^3 \quad\hbox{at}\quad (u, v) = (1, 1).$$

$u = 1$ and $v = 1$ give the point of tangency: $(x, y, z) = (-2, 4, 2)$ .

Next,

$$\vec{T}_u = \left(2 u, \dfrac{4}{v}, 4 u v^3\right) \quad\hbox{and}\quad \vec{T}_v = \left(-6 v, -\dfrac{4 u}{v^2}, 6 u^2 v^2\right).$$

Thus,

$$\vec{T}_u(1, 1) = (2, 4, 4) \quad\hbox{and}\quad \vec{T}_v(1, 1) = (-6, -4, 6).$$

The normal vector is given by

$$\vec{T}_u(1, 1) \times \vec{T}_v(1, 1) = \left|\matrix{ \ihat & \jhat & \khat \cr 2 & 4 & 4 \cr -6 & -4 & 6 \cr}\right| = (40, -36, 16).$$

The tangent plane is

$$40(x + 2) - 36(y - 4) + 16(z - 2) = 0, \quad\hbox{or}\quad 10 x - 9 y + 4 z = -48.\quad\halmos$$

13. Use a linear approximation to $z = f(x, y) = x^2 - y^2$ at the point $(2, 1)$ to approximate $f(1.9, 1.1)$ .

$f(2, 1) = 3$ , so the point of tangency is $(2, 1, 3)$ . A normal vector for a function $z = f(x, y)$ is given by

$$\vec N = \left( \pder f x, \pder f y, -1\right) = (2 x, -2 y, -1), \quad \vec{N}(2, 1) = (4, -2, -1).$$

Hence, the tangent plane is

$$4(x - 2) - 2(y - 1) - (z - 3) = 0, \quad\hbox{or}\quad z = 3 + 4(x - 2) - 2(y - 1).$$

Substitute $x = 1.9$ and $y = 1.1$ :

$$z = 3 + 4(-0.1) - 2(0.1) = 2.4.\quad\halmos$$

14. Let $f(x, y) = \dfrac{(x + 4)^2}{y}$ .

(a) Find a unit vector at $(-3, 1)$ which points in the direction of most rapid increase.

(b) Find the rate of most rapid increase at $(-3, 1)$ .

$$\nabla f (x, y) = \left(\dfrac{2 (x + 4)}{y}, -\dfrac{(x + 4)^2}{y^2}\right).$$

$$\nabla f (-3, 1) = (2, -1), \quad \|\nabla f (-3, 1)\| = \sqrt{5}.$$

(a) Find a unit vector at $(-3, 1)$ which points in the direction of most rapid increase is $\dfrac{1}{\sqrt{5}} (2, -1)$ .

(b) Find the rate of most rapid increase at $(-3, 1)$ is $\sqrt{5}$ .

15. Find the gradient of $f(x, y, z) = \dfrac{1}{\sqrt{x^2 + y^2 + z^2 + 1}}$ and show that it always points toward the origin.

$$\nabla f = \left( \dfrac{-x}{(x^2 + y^2 + z^2 + 1)^{3/2}}, \dfrac{-y}{(x^2 + y^2 + z^2 + 1)^{3/2}}, \dfrac{-z}{(x^2 + y^2 + z^2 + 1)^{3/2}}\right) =$$

$$\dfrac{-1}{(x^2 + y^2 + z^2 + 1)^{3/2}} (x, y, z).$$

$(x, y, z)$ is the radial vector from the origin $(0, 0, 0)$ to the point $(x, y, z)$ . Since $\nabla f$ is a negative multiple of this vector $\nabla f$ always points inward toward the origin.

16. Let $f(x, y) = \sqrt{x^2 + 2 y + 3}$ . Find the directional derivative of f at the point $(3, 2)$ in the direction of the vector $(-4, 3)$ .

$$\nabla f (x, y) = \left(\dfrac{x}{\sqrt{x^2 + 2 y + 3}}, \dfrac{1}{\sqrt{x^2 + 2 y + 3}}\right).$$

$$\nabla f (3, 2) = \left(\dfrac{3}{4}, \dfrac{1}{4}\right).$$

Hence,

$$Df_{(-4, 3)}(3, 2) = \left(\dfrac{3}{4}, \dfrac{1}{4}\right) \cdot \dfrac{(-4, 3)}{\|(-4, 3)\|} = \left(\dfrac{3}{4}, \dfrac{1}{4}\right) \cdot \dfrac{(-4, 3)}{5} = -\dfrac{9}{20}.\quad\halmos$$

17. Find the rate of change of $f(x, y, z) = x y - y z + x z$ at the point $(1, -2, -2)$ in the direction toward the origin. Is f increasing or decreasing in this direction?

First, compute the gradient at the point:

$$\nabla f = \left( y + z, x - z, -y + x\right), \quad \nabla f(1, -2, -2) = (-4, 3, 3).$$

Next, determine the direction vector. The point is $P(1, -2, -2)$ , so the direction toward the origin $Q(0, 0, 0)$ is

$$\bvec{P Q} = (-1, 2, 2).$$

Make this into a unit vector by dividing by its length:

$$\dfrac{\bvec{P Q}}{\|\bvec{PQ}\|} = \dfrac{1}{3} (-1, 2, 2).$$

Finally, take the dot product of the unit vector with the gradient:

$$Df_{\vec v}(1, -2, -2) = \nabla f(1, -2, -2)\cdot \dfrac{\bvec{PQ}}{\|\bvec{PQ}\|} = (-4, 3, 3) \cdot \dfrac{1}{3} (-1, 2, 2) = \dfrac{16}{3}.$$

f is increasing in this direction, since the directional derivative is positive.

18. The rate of change of $f(x, y)$ at $(1, -1)$ is 2 in the direction toward $(5, -1)$ and is $\dfrac{6}{5}$ in the direction of the vector $(-3, -4)$ . Find $\nabla f(1, -1)$ .

The direction from $(1, -1)$ toward the point $(5, -1)$ is given by the vector $(4, 0)$ . This vector has length 4, so

$$2 = \nabla f(1, -1) \cdot \dfrac{(4, 0)}{4} = (f_x, f_y) \cdot \dfrac{(4, 0)}{4} = f_x.$$

The vector $(-3, -4)$ has length 5, so

$$\dfrac{6}{5} = \nabla f(1, -1) \cdot \dfrac{(-3, -4)}{5} = (f_x, f_y) \cdot \dfrac{(-3, -4)}{5} = -\dfrac{3}{5} f_x - \dfrac{4}{5} f_y.$$

Thus, $6 = -3 f_x - 4 f_y$ .

I have two equations involving $f_x$ and $f_y$ . Solving simultaneously, I obtain $f_x = 2$ and $f_y = -3$ . Hence, $\nabla f(1, -1) = (2, -3)$ .

19. Calvin Butterball sits in his go-cart on the surface

$$z = x^3 - 2 x^2 y + x^2 + x y^2 - 2 y^3 + y^2 \quad\hbox{at the point}\quad (1, 1, 0).$$

If his go-cart is pointed in the direction of the vector $\vec v = (15, -8)$ , at what rate will it roll downhill?

The rate at which he rolls is given by the directional derivative. The gradient is

$$\nabla f = (3 x^2 - 4 x y + 2 x + y^2, -2 x^2 + 2 xy - 6 y^2 + 2 y ), \quad\hbox{and}\quad \nabla f(1, 1) = (2, -4).$$

Since $\|(15, -8)\| = 17$ ,

$$Df_{\vec v}(1, 1) = (2, -4) \cdot \dfrac{(15, -8)}{17} = \dfrac{62}{17} = 3.64705 \ldots.\quad\halmos$$

20. Find the tangent plane to $x^2 - y^2 + 2 y z + z^5 = 6$ at the point $(2, 1, 1)$ .

Write $w = x^2 - y^2 + 2 y z + z^5 - 6$ . (Take the original surface and drag everything to one side of the equation.) The original surface is $w = 0$ , so it's a level surface of w. Since the gradient $\nabla w$ is perpendicular to the level surfaces of w, it follows that $\nabla w$ must be perpendicular to the original surface.

The gradient is

$$\nabla w = (2 x, -2 y + 2 z, 2 y + 5 z^4), \quad \nabla w(2, 1, 1) = ( 4, 0, 7).$$

The vector $(4, 0, 7)$ is perpendicular to the tangent plane. Hence, the plane is

$$4 (x - 2) + 0 \cdot (y - 1) + 7 (z - 1) = 0, \quad\hbox{or}\quad 4 x + 7 z = 15.\quad\halmos$$

21. Suppose that $z = f(x, y)$ and $(x, y) = g(u, v)$ are given by

$$z = x^4 + 3 x y^2 - y^2, \quad (x, y) = (\sin 5 u + \cos v, \cos 3 u + \sin 2 v).$$

Find $\pder z u$ and $\pder z v$ .

$$\pder z u = \pder z x \pder x u + \pder z y \pder y u = (4 x^3 + 3 y^2)(5 \cos 5 u) + (6 x y - 2 y)(-3 \sin 3 u).$$

$$\pder z v = \pder z x \pder x v + \pder z y \pder y v = (4 x^3 + 3 y^2)(-\sin v) + (6 x y - 2 y)(2 \cos 2 v).\quad\halmos$$

22. Let r and $\theta$ be the standard polar coordinates variables. Use the Chain Rule to find $\pder f r$ and $\pder f \theta$ , for $f(x, y) = x e^x + e^y$ .

$$\pder f r = \pder f x \pder x r + \pder f y \pder y r = (x e^x + e^x)(\cos \theta) + (e^y)(\sin \theta),$$

$$\pder f \theta = \pder f x \pder x \theta + \pder f y \pder y \theta = (x e^x + e^x)(-r \sin \theta) + (e^y)(r \cos \theta).\quad\halmos$$

23. Suppose $u = f(x, y, z)$ and $x = \phi(s, t)$ , $y = \psi(s, t)$ , $z = \mu(s, t)$ . Use the Chain Rule to write down an expression for $\pder u t$ .

This diagram shows the dependence of the variables.

$$\hbox{\epsfysize=1.75 in \epsffile{rev2-1.eps}}$$

There are 3 paths from u to t, which give rise to the 3 terms in the following sum:

$$\pder u t = \pder u x \pder x t + \pder u y \pder y t + \pder u z \pder z t.\quad\halmos$$

24. Suppose that $w = f(x, y)$ , $x = g(r, s, t)$ , and $y = h(r, t, s)$ . Use the Chain Rule to find an expression for $\pdertwo f t$ .

By the Chain Rule,

$$\pder w t = \pder w x \pder x t + \pder w y \pder y t.$$

Next, differentiate with respect to t, applying the Product Rule to the terms on the right:

$$\pdertwo f t = \pder w x \pdertwo x t + \pder x t \pder {} t\left(\pder w x\right) + \pder w y \pdertwo y t + \pder y t \pder {} t\left(\pder w x\right).$$

Since $\pder w x$ and $\pder w y$ are functions of x and y, I must apply the Chain Rule in computing their derivatives with respect to t. I get

$$\pdertwo f t = \pder w x \pdertwo x t + \pder x t \left(\pder {} x \left(\pder w x\right) \pder x t + \pder {} y \left(\pder w x\right) \pder y t\right) + \pder w y \pdertwo y t + \pder y t \left(\pder {} x \left(\pder w y\right) \pder x t + \pder {} y \left(\pder w y\right) \pder y t\right) =$$

$$\pder w x \pdertwo x t + \pder x t \left(\pdertwo w x \pder x t + \pdertwom w x y \pder y t\right) + \pder w y \pdertwo y t + \pder y t \left(\pdertwom w x y \pder x t + \pdertwo w y \pder y t\right).\quad\halmos$$

25. Locate and classify the critical points of

$$z = x^2 y - 4 xy + \dfrac{1}{3}y^3 - \dfrac{3}{2}y^2.$$

$$\pder z x = 2 x y - 4 y, \quad \pder z y = x^2 - 4 x + y^2 - 3 y,$$

$$\pdertwo z x = 2 y, \quad \pdertwom z x y = 2 x - 4, \quad \pdertwo z y = 2 y - 3.$$

Set the first partials equal to 0:

$$2 x y - 4 y = 0, \quad (x - 2) y = 0.$$

$$x^2 - 4 x + y^2 - 3 y = 0.$$

Solve simultaneously:

$$\matrix{ & & & & (x - 2) y = 0 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & x = 2 & & & & y = 0 & & \cr & & x^2 - 4 x + y^2 - 3 y = 0 & & & & x^2 - 4 x + y^2 - 3 y = 0 & & \cr & & y^2 - 3 y - 4 = 0 & & & & x^2 - 4 x = 0 & & \cr & & (y - 4)(y + 1) = 0 & & & & x(x - 4) = 0 & & \cr & \swarrow & \downarrow & & & & \downarrow & \searrow & \cr y = 4 & & y = -1 & & & & x = 0 & & x = 4 \cr (2, 4) & & (2, -1) & & & & (0, 0) & & (4, 0) \cr}$$

Test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $z_{x x}$ & & $z_{y y}$ & & $z_{x y}$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(2, 4)$ & & 8 & & 5 & & 0 & & 40 & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(2, -1)$ & & -2 & & -5 & & 0 & & 10 & & max & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & 0 & & -3 & & -4 & & -16 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(4, 0)$ & & 0 & & -3 & & 4 & & -16 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

26. Locate and classify the critical points of

$$f(x, y) = 6 x y^2 - 2 x^3 y + y^2.$$

$$f_x = 6 y^2 - 6 x^2 y, \quad f_y = 12 x y - 2 x^3 + 2 y,$$

$$f_{x x} = -12 x y, \quad f_{x y} = 12 y - 6 x^2, \quad f_{y y} = 12 x + 2.$$

Set the first partials equal to 0:

$$6 y^2 - 6 x^2 y = 0, \quad y(y - x^2) = 0, \leqno{\rm (1)}$$

$$12 x y - 2 x^3 + 2 y = 0, \quad 6 x y - x^3 + y = 0. \leqno{\rm (2)}$$

Solve simultaneously:

$$\matrix{ & & {\rm (1)} & y(y - x^2) = 0 & & & & \cr & & \swarrow & & \searrow & & & \cr & y = 0 & & & & y = x^2 & & \cr {\rm (2)} & 6 x y - x^3 + y = 0 & & & {\rm (2)} & 6 x y - x^3 + y = 0 & & \cr & x^3 = 0 & & & & 6 x^3 - x^3 + x^2 = 0 & & \cr & x = 0 & & & & 5 x^3 + x^2 = 0 & & \cr & (0, 0) & & & & x^2(5 x + 1) = 0 & & \cr & & & & \swarrow & & \searrow & \cr & & & x^2 = 0 & & & & 5 x + 1 = 0 \cr & & & x = 0 & & & & x = -\dfrac{1}{5} \cr & & & y = 0 & & & & y = \dfrac{1}{25} \cr & & & (0, 0) & & & & \left(-\dfrac{1}{5}, \dfrac{1}{25}\right) \cr}$$

\overfullrule=0 pt

Test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $f_{x x} = -12 x y$ & & $f_{y y} = 12 x + 2$ & & $f_{x y} = 12 y - 6 x^2$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & 0 & & 2 & & 0 & & 0 & & test fails & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\left(-\dfrac{1}{5}, \dfrac{1}{25}\right)$ & & $\dfrac{12}{125}$ & & $-\dfrac{2}{5}$ & & $\dfrac{6}{25}$ & & $-\dfrac{12}{125}$ & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

27. Find the critical points of

$$z = (x^2 + y^2) e^{-x^2 - 4 y^2}.$$

You do not need to classify them.

$$z_x = -2 x(x^2 + y^2) e^{-x^2-4 y^2} + 2 x e^{-x^2-4 y^2} = -2 x(x^2 + y^2 - 1) e^{-x^2-4 y^2},$$

$$z_y = -8 y(x^2 + y^2) e^{-x^2-4 y^2} + 2 y e^{-x^2-4 y^2} = -2 y(4 x^2 + 4 y^2 - 1) e^{-x^2-4 y^2}.$$

Set the first partials equal to 0:

$$-2 x (x^2 + y^2 - 1) e^{-x^2-4 y^2} = 0, \quad x (x^2 + y^2 - 1) = 0.$$

$$-2 y (4 x^2 + 4 y^2 - 1) e^{-x^2-4 y^2} = 0, \quad y (4 x^2 + 4 y^2 - 1) = 0.$$

Solve simultaneously:

$$\matrix{ & & & x (x^2 + y^2 - 1) = 0 & & \cr & & \swarrow & & \searrow & \cr & x = 0 & & & & x^2 + y^2 = 1 \cr & y (4 x^2 + 4 y^2 - 1) = 0 & & & & y (4 x^2 + 4 y^2 - 1) = 0 \cr & y(4 y^2 - 1) = 0 & & & & 3 y = 0 \cr & {\rm (A)} & & & & {\rm (B)} \cr}$$

$$\matrix{ & & {\rm (A)} & & \cr & & y (4 y^2 - 1) = 0 & & \cr & \swarrow & & \searrow & \cr y = 0 & & & & 4 y^2 - 1 = 0 \cr (0, 0) & & & & \matrix{& \swarrow & & \searrow & \cr y = \dfrac{1}{2} & & & & y = -\dfrac{1}{2} \cr \left(0,\dfrac{1}{2}\right) & & & & \left(0, -\dfrac{1}{2}\right) \cr} \cr}$$

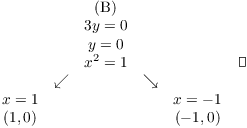
$$\matrix{ & & {\rm (B)} & & \cr & & 3 y = 0 & & \cr & & y = 0 & & \cr & & x^2 = 1 & & \cr & \swarrow & & \searrow & \cr x = 1 & & & & x = -1 \cr (1, 0) & & & & (-1, 0) \cr}\quad\halmos$$

28. Find the points on the sphere $x^2 + y^2 + z^2 = 36$ which are closest to and farthest from the point $(4, -3, 12)$ .

The (square of the) distance from $(x, y, z)$ to $(4, -3, 12)$ is

$$w = (x - 4)^2 + (y + 3)^2 + (z - 12)^2.$$

The constraint is $g(x, y, z) = x^2 + y^2 + z^2 - 36 = 0$ .

The equations to be solved are

$$2 (x - 4) = 2 x\lambda, \quad x - 4 = x\lambda.$$

$$2 (y + 3) = 2 y\lambda, \quad y + 3 = y\lambda.$$

$$2 (z - 12) = 2 z\lambda, \quad z - 12 = z\lambda.$$

$$x^2 + y^2 + z^2 = 36.$$

Note that if $x = 0$ in the first equation, the equation becomes $-4 = 0$ , which is impossible. Therefore, $x \ne 0$ , and I may divide by x.

Solve simultaneously:

$$\matrix{ & & x - 4 = x\lambda & & \cr & & \lambda = \dfrac{x - 4}{x} & & \cr & & y + 3 = y\lambda & & \cr & & y + 3 = \dfrac{y(x - 4)}{x} & & \cr & & xy + 3 x = yx - 4 y & & \cr & & y = -\dfrac{3}{4}x & & \cr & & z - 12 = z\lambda & & \cr & & z - 12 = \dfrac{z(x - 4)}{x} & & \cr & & xz - 12 x = xz - 4 z & & \cr & & z = 3 x & & \cr & & x^2 + y^2 + z^2 = 36 & & \cr & & x^2 + \dfrac{9}{16} x^2 + 9 x^2 = 36 & & \cr & & 169 x^2 = 576 & & \cr & & x^2 = \dfrac{576}{169} & & \cr & \swarrow & & \searrow & \cr x = \dfrac{24}{13} & & & & x = -\dfrac{24}{13}\cr y = -\dfrac{18}{13} & & & & y = \dfrac{18}{13}\cr z = \dfrac{72}{13} & & & & z = -\dfrac{72}{13}\cr \left(\dfrac{24}{13}, -\dfrac{18}{13},\dfrac{72}{13}\right) & & & & \left(-\dfrac{24}{13},\dfrac{18}{13}, -\dfrac{72}{13}\right) \cr}$$

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & & & $\left(\dfrac{24}{13}, -\dfrac{18}{13},\dfrac{72}{13}\right)$ & & $\left(-\dfrac{24}{13},\dfrac{18}{13}, -\dfrac{72}{13}\right)$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $w(x, y, z)$ & & 49 & & 361 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$\left(\dfrac{24}{13}, -\dfrac{18}{13},\dfrac{72}{13}\right)$ is closest to $(4, -3, 12)$ and $\left(-\dfrac{24}{13},\dfrac{18}{13}, -\dfrac{72}{13}\right)$ is farthest from $(4, -3, 12)$ .

29. A rectangular box (with a bottom and a top) is to have a total surface area of $6 c^2$ , where $c > 0$ . Show that the box of largest volume satisfying this condition is a cube with sides of length c.

Suppose the dimensions of the box are x, y, and z. Then the volume is

$$V = x y z.$$

The surface area is

$$6 c^2 = 2 x y + 2 y z + 2 x z, \quad\hbox{so}\quad 3 c^2 = x y + y z + x z.$$

The constraint is

$$g(x, y, z) = x y + y z + x z - 3 c^2 = 0.$$

Set up the multiplier equation:

$$\eqalign{ \nabla V & = \lambda \nabla g \cr (y z, x z, x y) & = \lambda (y + z, x + z, x + y) \cr}$$

This gives the equations

$$y z = \lambda (y + z).$$

$$x z = \lambda (x + z).$$

$$x y = \lambda (x + y).$$

$$3 c^2 = x y + y z + x z.$$

Note that $x = y = z = c$ satisfies the constraint and gives a volume of $c^3$ . Thus, the solution to the problem certainly has $V > 0$ . If any of x, y, or z is 0, the volume is 0, which is not a max. So I may assume $x, y, z > 0$ .

Note that this also implies that $y + z > 0$ , so I may divide by $y + z$ .

Now solve the equations:

$$\eqalign{ y z & = \lambda (y + z) \cr \noalign{\vskip2pt} \lambda = \dfrac{y z}{y + z} \cr \noalign{\vskip2pt} x z & = \lambda (x + z) \cr \noalign{\vskip2pt} x z & = \dfrac{y z}{y + z} (x + z) \cr \noalign{\vskip2pt} x z (y + z) & = y z (x + z) \cr x y z + x z^2 & = x y z + y z^2 \cr x z^2 & = y z^2 \cr x & = y \cr}$$

$$\eqalign{ x y & = \lambda (x + y) \cr \noalign{\vskip2pt} x y & = \dfrac{y z}{y + z} (x + y) \cr \noalign{\vskip2pt} x y (y + z) & = y z (x + y) \cr x y^2 + x y z & = x y z + y^2 z \cr x y^2 & = y^2 z \cr x & = z \cr 3 c^2 & = x y + y z + x z \cr 3 c^2 & = x^2 + x^2 + x^2 \cr x & = c \cr y & = c \cr z & = c \cr}$$

The critical point is $(c, c, c)$ , which is a cube with sides of length c.

30. (a) Find the critical points of

$$w = 4 x y z \quad\hbox{subject to the constraint}\quad x + y + z = 3.$$

(b) Express w as a function of x and y by eliminating z, then consider the behavior of w for $x = y$ . Explain why the critical points in (a) can't give absolute maxes or mins.

The constraint is

$$g(x, y, z) = x + y + z - 3 = 0.$$

Set up the multiplier equation:

$$\eqalign{ \nabla f & = \lambda \nabla g \cr (4 y z, 4 x z, 4 x y) & = \lambda (1, 1, 1) \cr}$$

This gives the equations

$$4 y z = \lambda.$$

$$4 x z = \lambda.$$

$$4 x y = \lambda.$$

$$x + y + z = 3.$$

Solve the equations:

$$\matrix{ & & & & 4 y z = \lambda & & & & \cr & & & & 4 x z = \lambda & & & & \cr & & & & 4 y z = 4 x z & & & & \cr & & & & y z - x z = 0 & & & & \cr & & & & (y - x) z = 0 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & y = x & & & & z = 0 & & \cr & & 4 x y = \lambda & & & & \lambda = 0 & & \cr & & 4 x y = 4 x z & & & & 4 x y = 0 & & \cr & & x y - x z = 0 & & & & x y = 0 & & \cr & & x(y - z) = 0 & & & & \downarrow & \searrow & \cr & \swarrow & \downarrow & & & & x = 0 & & y = 0 \cr x = 0 & & y = z & & & & x + y + z = 3 & & x + y + z = 3 \cr y = 0 & & x + y + z = 3 & & & & y = 3 & & x = 3 \cr x + y + z = 3 & & 3 x = 3 & & & & (0, 3, 0) & & (3, 0, 0) \cr \noalign{\vskip2pt} z = 3 & & x = 1 & & & & & & \cr \noalign{\vskip2pt} (0, 0, 3) & & y = 1 & & & & & & \cr \noalign{\vskip2pt} & & z = 1 & & & & & & \cr \noalign{\vskip2pt} & & \left(1, 1, 1\right) & & & & & & \cr}$$

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & point & & $w = 4 x y z$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $(3, 0, 0)$ & & 0 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $(0, 3, 0)$ & & 0 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $(0, 0, 3)$ & & 0 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $\left(1, 1, 1\right)$ & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

(b) Solving the constraint for z gives $z = 3 - x - y$ . Then

$$w = 4 x y (3 - x - y).$$

Consider the behavior of w along the line $x = y$ :

$$w = 4 x^2 (3 - 2 x).$$

The factor $4 x^2$ is positive. As $x \to infty$ , the term $3 - 2 x$ becomes large and negative, so $w \to -\infty$ . As $x \to -\infty$ , the term $3 - 2 x$ becomes large and positive, so $w \to \infty$ .

This means that you can find values of x, y, and z satisfying the constraint for which w is arbitrarily big or small. Hence, the critical points found in (a) can't be absolute maxes or mins.

31. Find the largest and smallest values of $f(x,y) = 4 x^2 y$ subject to the constraint $x^2 + y^2 = 36$ .

The constraint is $g(x,y) = x^2 + y^2 - 36 = 0$ .

Set up the multiplier equation:

$$\eqalign{ \nabla f & = \lambda \nabla g \cr (8 x y, 4 x^2) & = \lambda (2 x, 2 y) \cr}$$

This gives two equations:

$$8 x y = 2 x \lambda, \quad 4 x y = x \lambda = 0, \quad x(4 y - \lambda) = 0.$$

$$4 x^2 = 2 y \lambda.$$

Solve those equations simultaneously with the constraint:

$$\matrix{ & & & & x(4 y - \lambda) = 0 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & x = 0 & & & & \lambda = 4 y & & \cr & & x^2 + y^2 = 36 & & & & 4 x^2 = 2 y \lambda & & \cr & & y^2 = 36 & & & & 4 x^2 = 2 y \cdot 4 y & & \cr & \swarrow & \downarrow & & & & x^2 = 2 y^2 & & \cr \noalign{\vskip2pt} y = 6 & & y = -6 & & & & 2 y^2 + y^2 = 36 & & \cr (0, 6) & & (0, -6) & & & & 3 y^2 = 36 & & \cr \noalign{\vskip2pt} & & & & & & y^2 = 12 & & \cr \noalign{\vskip2pt} & & & & & \swarrow & \downarrow & & \cr \noalign{\vskip2pt} & & & & y = 2 \sqrt{3} & & y = -2 \sqrt{3} & & \cr \noalign{\vskip2pt} & & & & x^2 = 24 & & x^2 = 24 & & \cr \noalign{\vskip2pt} & & & \swarrow & \downarrow & & \downarrow & \searrow & \cr \noalign{\vskip2pt} & & x = 2 \sqrt{6} & & x = -2 \sqrt{6} & & x = 2 \sqrt{6} & & x = -2 \sqrt{6} \cr \noalign{\vskip2pt} & & \left(2 \sqrt{6}, 2 \sqrt{3}\right) & & \left(-2 \sqrt{6}, 2 \sqrt{3}\right) & & \left(2 \sqrt{6}, -2 \sqrt{3}\right) & & \left(-2 \sqrt{6}, -2 \sqrt{3}\right) \cr}$$

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \ # \ \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & $(0, 6)$ & & $(0, -6)$ & & $\left(2 \sqrt{6}, 2 \sqrt{3}\right)$ & & $\left(-2 \sqrt{6}, 2 \sqrt{3}\right)$ & & $\left(2 \sqrt{6}, -2 \sqrt{3}\right)$ & & $\left(-2 \sqrt{6}, -2 \sqrt{3}\right)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $f(x, y)$ & & 0 & & 0 & & $192 \sqrt{3}$ & & $192 \sqrt{3}$ & & $-192 \sqrt{3}$ & & $-192 \sqrt{3}$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & max & & max & & min & & min & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

To be conscious that you are ignorant is a great step to knowledge. - Benjamin Disraeli

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga