Cyclic Groups

Cyclic groups are groups in which every element is a power of some fixed element. (If the group is abelian and I'm using + as the operation, then I should say instead that every element is a multiple of some fixed element.) Here are the relevant definitions.

Definition. Let G be a group, $g \in G$ . The order of g is the smallest positive integer n such that $g^n = 1$ . If there is no positive integer n such that $g^n = 1$ , then g has infinite order.

In the case of an abelian group with + as the operation and 0 as the identity, the order of g is the smallest positive integer n such that $ng = 0$ .

Definition. If G is a group and $g \in G$ , then the subgroup generated by g is

$$\langle g \rangle = \{g^n \mid n \in \integer\}.$$

If the group is abelian and I'm using + as the operation, then

$$\langle g \rangle = \{n g \mid n \in \integer\}.$$

Definition. A group G is cyclic if $G = \langle g \rangle$ for some $g \in G$ . g is a generator of $\langle g \rangle$ .

If a generator g has order n, $G = \langle g\rangle$ is cyclic of order n. If a generator g has infinite order, $G = \langle g\rangle$ is infinite cyclic.

Example. ( The integers and the integers mod n are cyclic) Show that $\integer$ and $\integer_n$ for $n > 0$ are cyclic.

$\integer$ is an infinite cyclic group, because every element is a multiple of 1 (or of -1). For instance, $117 = 117 \cdot 1$ .

(Remember that "$117 \cdot 1$ " is really shorthand for $1 + 1 + \cdots + 1$ --- 1 added to itself 117 times.)

In fact, it is the only infinite cyclic group up to isomorphism.

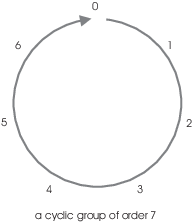
Notice that a cyclic group can have more than one generator.

If n is a positive integer, $\integer_n$ is a cyclic group of order n generated by 1.

For example, 1 generates $\integer_7$ , since

$$\eqalign{ 1 + 1 &= 2 \cr 1 + 1 + 1 &= 3 \cr 1 + 1 + 1 + 1 &= 4 \cr 1 + 1 + 1 + 1 + 1 &= 5 \cr 1 + 1 + 1 + 1 + 1 + 1 &= 6 \cr 1 + 1 + 1 + 1 + 1 + 1 + 1 &= 0 \cr}$$

In other words, if you add 1 to itself repeatedly, you eventually cycle back to 0.

$$\hbox{\epsfysize=2 in \epsffile{cyclic-groups-1.eps}}$$

Notice that 3 also generates $\integer_7$ :

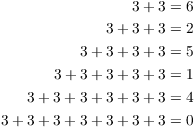
$$\eqalign{ 3 + 3 &= 6 \cr 3 + 3 + 3 &= 2 \cr 3 + 3 + 3 + 3 &= 5 \cr 3 + 3 + 3 + 3 + 3 &= 1 \cr 3 + 3 + 3 + 3 + 3 + 3 &= 4 \cr 3 + 3 + 3 + 3 + 3 + 3 + 3 &= 0 \cr}$$

The "same" group can be written using multiplicative notation this way:

$$\integer_7 = \{1, a, a^2, a^3, a^4, a^5, a^6\}.$$

In this form, a is a generator of $\integer_7$ .

It turns out that in $\integer_7 = \{0, 1, 2, 3, 4, 5, 6\}$ , every nonzero element generates the group.

On the other hand, in $\integer_6 = \{0, 1, 2, 3, 4, 5\}$ , only 1 and 5 generate.

Lemma. Let $G = \langle g \rangle$ be a finite cyclic group, where g has order n. Then the powers $\{1, g, \ldots, g^{n-1}\}$ are distinct.

Proof. Since g has order n, g, $g^2$ , ... $g^{n-1}$ are all different from 1.

Now I'll show that the powers $\{1, g, \ldots, g^{n-1}\}$ are distinct. Suppose $g^i = g^j$ where $0 \le j < i < n$ . Then $0 < i - j < n$ and $g^{i-j} = 1$ , contrary to the preceding observation.

Therefore, the powers $\{1, g, \ldots, g^{n-1}\}$ are distinct.

Lemma. Let $G = \langle g\rangle$ be infinite cyclic. If m and n are integers and $m \ne n$ , then $g^m \ne g^n$ .

Proof. One of m, n is larger --- suppose without loss of generality that $m > n$ . I want to show that $g^m \ne g^n$ ; suppose this is false, so $g^m = g^n$ . Then $g^{m-n} = 1$ , so g has finite order. This contradicts the fact that a generator of an infinite cyclic group has infinite order. Therefore, $g^m \ne g^n$ .

The next result characterizes subgroups of cyclic groups. The proof uses the Division Algorithm for integers in an important way.

Theorem. Subgroups of cyclic groups are cyclic.

Proof. Let $G = \langle g\rangle$ be a cyclic group, where $g \in G$ . Let $H < G$ . If $H = \{1\}$ , then H is cyclic with generator 1. So assume $H \ne \{ 1\}$ .

To show H is cyclic, I must produce a generator for H. What is a generator? It is an element whose powers make up the group. A thing should be smaller than things which are "built from" it --- for example, a brick is smaller than a brick building. Since elements of the subgroup are "built from" the generator, the generator should be the "smallest" thing in the subgroup.

What should I mean by "smallest"?

Well, G is cyclic, so everything in G is a power of g. With this discussion as motivation, let m be the smallest positive integer such that $g^m \in H$ .

Why is there such an integer m? Well, H contains something other than $1 = g^0$ , since $H \ne \{1\}$ . That "something other" is either a positive or negative power of g. If H contains a positive power of g, it must contain a smallest positive power, by well ordering.

On the other hand, if H contains a negative power of g --- say $g^{-k}$ , where $k > 0$ --- then $g^k \in H$ , since H is closed under inverses. Hence, H again contains positive powers of g, so it contains a smallest positive power, by Well Ordering.

So I have $g^m$ , the smallest positive power of g in H. I claim that $g^m$ generates H. I must show that every $h \in H$ is a power of $g^k$ . Well, $h \in H < G$ , so at least I can write $h = g^n$ for some n. But by the Division Algorithm, there are unique integers q and r such that

$$n = m q + r, \quad\hbox{where}\quad 0 \le r < m.$$

It follows that

$$g^n = g^{m q + r} = (g^m)^q \cdot g^r, \quad\hbox{so}\quad h = (g^m)^q \cdot g^r, \quad\hbox{or}\quad g^r = (g^m)^{-q} \cdot h.$$

Now $g^m \in H$ , so $(g^m)^{-q} \in H$ . Hence, $(g^m)^{-q} \cdot h \in H$ , so $g^r \in H$ . However, $g^m$ was the smallest positive power of g lying in H. Since $g^r \in H$ and $r < m$ , the only way out is if $r = 0$ . Therefore, $n = q m$ , and $h = g^n = (g^m)^q \in \langle g^m\rangle$ .

This proves that $g^m$ generates H, so H is cyclic.

Example. ( Subgroups of the integers) Describe the subgroups of $\integer$ .

Every subgroup of $\integer$ has the form $n\integer$ for $n \in \integer$ .

For example, here is the subgroup generated by 13:

$$13 \integer = \langle 13 \rangle = \{\ldots -26, -13, 0, 13, 26, \ldots \}.\quad\halmos$$

Example. Consider the following subset of $\integer$ :

$$H = \{30 x + 42 y + 70 z \mid x, y, z \in \integer\}.$$

(a) Prove that H is a subgroup of $\integer$ .

(b) Find a generator for H.

(a) First,

$$0 = 30 \cdot 0 + 42 \cdot 0 + 70 \cdot 0 \in H.$$

If $30 x + 42 y + 70 z \in H$ , then

$$-(30 x + 42 y + 70 z) = 30 (-x) + 42 (-y) + 70 (-z) \in H.$$

If $30 a + 42 b + 70 c, 30 d + 42 e + 70 f \in H$ , then

$$(30 a + 42 b + 70 c) + (30 d + 42 e + 70 f) = 30(a + d) + 42 (b + e) + 70 (c + f) \in H.$$

Hence, H is a subgroup.

(b) Note that $2 = (30, 42, 70)$ . I'll show that $H = \langle 2 \rangle$ .

First, if $30 x + 42 y + 70 z \in H$ , then

$$30 x + 42 y + 70 z = 2(15 x + 21 y + 35 z) \in \langle 2 \rangle.$$

Therefore, $H \subset \langle 2 \rangle$ .

Conversely, suppose $2 n \in \langle 2 \rangle$ . I must show $2 n \in H$ .

The idea is to write 2 as a linear combination of 30, 42, and 70. I'll do this in two steps.

First, note that $(30, 42) = 6$ , and

$$30 \cdot 3 + 42 \cdot (-2) = 6.$$

(You can do this by juggling numbers or using the Extended Euclidean algorithm.) Now $(6, 70) = 2$ , and

$$6 \cdot 12 + 70 \cdot (-1) = 2.$$

Plugging $6 = 30 \cdot 3 + 42 \cdot (-2)$ into the last equation, I get

$$\eqalign{ (30 \cdot 3 + 42 \cdot (-2)) \cdot 12 + 70 \cdot (-1) & = 2 \cr 30 \cdot 36 + 42 \cdot (-24) + 70 \cdot (-1) & = 2 \cr}$$

Now multiply the last equation by n:

$$2 n = 30 \cdot 36 n + 42 \cdot (-24 n) + 70 \cdot (-n) \in H.$$

This shows that $\langle 2 \rangle \subset H$ .

Therefore, $H = \langle 2 \rangle$ .

Lemma. Let G be a group, and let $g \in G$ have order m. Then $g^n = 1$ if and only if m divides n.

Proof. If m divides n, then $n = m q$ for some q, so $g^n = (g^m)^q = 1$ .

Conversely, suppose that $g^n = 1$ . By the Division Algorithm,

$$n = m q + r \quad\hbox{where}\quad 0 \le r < m.$$

Hence,

$$g^n = g^{m q + r} = (g^m)^qg^r \quad\hbox{so}\quad 1 = g^r.$$

Since m is the smallest positive power of g which equals 1, and since $r < m$ , this is only possible if $r = 0$ . Therefore, $n = qm$ , which means that m divides n.

Example. ( The order of an element) Suppose an element g in a group G satisfies $g^{45} = 1$ . What are the possible values for the order of g?

The order of g must be a divisor of 45. Thus, the order could be

$$1, \quad 3, \quad 5, \quad 9, \quad 15, \quad\hbox{or}\quad 45.$$

And the order is certainly not (say) 7, since 7 doesn't divide 45.

Thus, the order of an element is the smallest power which gives the identity the element in two ways. It is smallest in the sense of being numerically smallest, but it is also smallest in the sense that it divides any power which gives the identity.

Next, I'll find a formula for the order of an element in a cyclic group.

Proposition. Let $G = \langle g\rangle$ be a cyclic group of order n, and let $m < n$ . Then $g^m$ has order $\dfrac{n}{(m, n)}$ .

Remark. Note that the order of $g^m$ (the element) is the same as the order of $\langle g^m \rangle$ (the subgroup).

Proof. Since $(m, n)$ divides m, it follows that $\dfrac{m}{(m, n)}$ is an integer. Therefore, n divides $\dfrac{mn}{(m, n)}$ , and by the last lemma,

$$(g^m)^{\frac{n}{(m, n)}} = 1.$$

Now suppose that $(g^m)^k = 1$ . By the preceding lemma, n divides $mk$ , so

$$\dfrac{n}{(m, n)} \Bigm| k \cdot \dfrac{m}{(m, n)}.$$

However, $\left(\dfrac{n}{(m, n)},\dfrac{m}{(m, n)}\right) = 1$ , so $\dfrac{n}{(m, n)}$ divides k. Thus, $\dfrac{n}{(m, n)}$ divides any power of $g^m$ which is 1, so it is the order of $g^m$ .

In terms of $\integer_n$ , this result says that $m \in \integer_n$ has order $\dfrac{n}{(m, n)}$ .

Example. ( Finding the order of an element) Find the order of the element $a^{32}$ in the cyclic group $G = \{1, a, a^2, \ldots a^{37}\}$ . (Thus, G is cyclic of order 38 with generator a.)

In the notation of the Proposition, $n = 38$ and $m = 32$ . Since $(38, 32) = 2$ , it follows that $a^{32}$ has order $\dfrac{38}{2} = 19$ .

Example. ( Finding the order of an element) Find the order of the element $18 \in \integer_{30}$ .

In this case, I'm using additive notation instead of multiplicative notation. The group is cyclic with order $n = 30$ , and the element $18 \in \integer_{30}$ corresponds to $a^{18}$ in the Proposition --- so $m = 18$ .

$(18, 30) = 6$ , so the order of 18 is $\dfrac{30}{6} = 5$ .

Next, I'll give two important Corollaries of the proposition.

Corollary. The generators of $\integer_n = \{0, 1, 2, \ldots, n - 1\}$ are the elements of $\{0, 1, 2, \ldots, n - 1\}$ which are relatively prime to n.

Proof. If $m \in \{0, 1, 2, \ldots, n - 1\}$ is a generator, its order is n. The Proposition says its order is $\dfrac{n}{(m, n)}$ . Therefore, $n = \dfrac{n}{(m, n)}$ , so $(m, n) = 1$ .

Conversely, if $(m, n) = 1$ , then the order of m is

$$\dfrac{n}{(m, n)} = \dfrac{n}{1} = n.$$

Therefore, m is a generator of $\integer_n$ .

Example. ( Finding the generators of a cyclic group) List the generators of:

(a) $\integer_{12}$ .

(b) $\integer_p$ , where p is prime.

(a) The generators of $\integer_{12}$ are 1, 5, 7, and 11. These are the elements of $\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}$ which are relatively prime to 12.

(b) If p is prime, the generators of $\integer_p$ are 1, 2, ..., $p - 1$ .

Example. (a) List the generators of $\integer_9$ .

(b) List the elements of the subgroup $\langle 3 \rangle$ of $\integer_{27}$ .

(c) List the generators of the subgroup $\langle 3 \rangle$ of $\integer_{27}$ .

(a) The generators are the elements relatively prime to 9, namely 1, 2, 4, 5, 7, and 8.

(b)

$$\langle 3 \rangle = \{0, 3, 6, 9, 12, 15, 18, 21, 24\}.\quad\halmos$$

(c) $\langle 3 \rangle$ is cyclic of order 9, so its generators are the elements corresponding to the generators 1, 2, 4, 5, 7, and 8 of $\integer_9$ . Since $27 = 3 \cdot 9$ , I can just multiply these generators by 3.

Thus, the generators of $\langle 3 \rangle$ are 3, 6, 12, 15, 21, and 24.

Corollary. A finite cyclic group of order n contains a subgroup of order m for each positive integer m which divides n.

Proof. Suppose G is a finite cyclic group of order n with generator g, and suppose $m \mid n$ . Thus, $mp = n$ for some p.

I claim that $g^p$ generates a subgroup of order m. The preceding proposition says that the order of $g^p$ is $\dfrac{n}{(p, n)}$ . However, $p \mid n$ , so $(p, n) = p$ . Therefore, $g^p$ has order

$$\dfrac{n}{(p, n)} = \dfrac{n}{p} = m.$$

In other words, $g^p$ generates a subgroup of order m.

In fact, it's possible to prove that there is a unique a subgroup of order m for each m dividing n.

Note that for an arbitrary finite group G, it isn't true that if $n \mid |G|$ , then G contains a cyclic subgroup of order n.

Example. ( Subgroups of a cyclic group) (a) List the subgroups of $\integer_{15}$ .

(b) List the subgroups of $\integer_{24}$ .

(a) $\integer_{15}$ contains subgroups of order 1, 3, 5, and 15, since these are the divisors of 15. The subgroup of order 1 is the identity, and the subgroup of order 15 is the entire group.

The last result says: If n divides 15, then there is a subgroup of order n --- in fact, a unique subgroup of order n.

Since $\integer_{15}$ is cyclic, these subgroups must be cyclic. They are generated by 0 and the nonzero elements in $\integer_{15}$ which divide 15: 1, 3, and 5.

Lagrange's theorem (which I'll discuss later) says that in any finite group, the order of a subgroup must divide the order of the group. In this context, Lagrange's theorem says if H is a subgroup of order n, then n divides 15.

Putting these results together, this means that you can find all the subgroups of $\integer_{15}$ by taking $\{0\}$ (the trivial subgroup), together with the cyclic subgroups generated by the nonzero elements in $\integer_{15}$ which divide 15: 1, 3, and 5.

1 generates $\integer_{15}$ .

5 generates a subgroup of order 3:

$$\langle 5 \rangle = \{0, 5, 10\}.$$

3 generates a subgroup of order 5:

$$\langle 3 \rangle = \{0, 3, 6, 9, 12\}.\quad\halmos$$

(b) Since the divisors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24, the subgroups of $\integer_{24}$ are:

$$\langle 0 \rangle, \quad \langle 1 \rangle, \quad \langle 2 \rangle, \quad \langle 3 \rangle, \quad \langle 4 \rangle, \quad \langle 6 \rangle, \quad \langle 8 \rangle, \quad \langle 12 \rangle.$$

The subgroup generated by 3 has order 8:

$$\langle 3 \rangle = \{0, 3, 6, 9, 12, 15, 18, 21\}.\quad\halmos$$

Example. ( A product of cyclic groups) Consider the group

$$\integer_2 \times \integer_3 = \{(m, n) \mid m \in \integer_2, n \in \integer_3\}.$$

Show that $\integer_2 \times \integer_3$ is cyclic by finding a generator.

The operation is componentwise addition:

$$(m, n) + (m', n') = (m + m', n + n').$$

It is routine to verify that this is a group, the direct product of $\integer_2$ and $\integer_3$ .

The element $(1, 1) \in \integer_2 \times \integer_3$ has order 6:

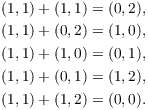
$$\eqalign{ (1, 1) + (1, 1) &= (0, 2),\cr (1, 1) + (0, 2) &= (1, 0),\cr (1, 1) + (1, 0) &= (0, 1),\cr (1, 1) + (0, 1) &= (1, 2),\cr (1, 1) + (1, 2) &= (0, 0).\cr } $$

Hence, $\integer_2 \times \integer_3$ is cyclic of order 6. More generally, if $(m, n) = 1$ , then $\integer_m \times \integer_n$ is cyclic of order $m n$ . Be careful! --- $\integer_2 \times \integer_2$ is not the same as $\integer_4$ !

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga