The First Isomorphism Theorem

The First Isomorphism Theorem helps identify quotient groups as "known" or "familiar" groups.

I'll begin by proving a useful lemma.

Proposition. Let $\phi: G \rightarrow H$ be a group map. $\phi$ is injective if and only if $\ker \phi = \{1\}$ .

Proof. ( $\rightarrow$ ) Suppose $\phi$ is injective. Since $\phi(1) = 1$ , $\{1\} \subset \ker\phi$ . Conversely, let $g \in \ker\phi$ , so $\phi(g) = 1$ . Then $\phi(g) = 1 = \phi(1)$ , so by injectivity . Therefore, $\ker\phi \subset \{1\}$ , so $\ker\phi = \{1\}$ .

( $\ifthen$ ) Suppose $\ker \phi = \{1\}$ . I want to show that $\phi$ is injective. Suppose $\phi(a) = \phi(b)$ . I want to show that .

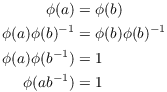
$\eqalign{ \phi(a) & = \phi(b) \cr \phi(a) \phi(b)^{-1} & = \phi(b) \phi(b)^{-1} \cr \phi(a) \phi(b^{-1}) & = 1 \cr \phi(a b^{-1}) & = 1 \cr}$

Hence, $a b^{-1} \in \ker \phi = \{1\}$ , so $a b^{-1} = 1$ , and . Therefore, $\phi$ is injective.

Example. ( Proving that a group map is injective) Define $f: \real^2 \to \real^2$ by

Prove that f is injective.

As usual, $\real^2$ is a group under vector addition. I can write f in the form

$f\left(\left[\matrix{x \cr y \cr}\right]\right) = \left[\matrix{3 & 2 \cr 1 & 1 \cr}\right] \left[\matrix{x \cr y \cr}\right].$

Since f has been represented as multiplication by a constant matrix, it is a linear transformation, so it's a group map.

To show f is injective, I'll show that the kernel of f consists of only the identity: $\ker f = \{(0, 0)\}$ . Suppose $(x, y) \in \ker f$ . Then

$\left[\matrix{3 & 2 \cr 1 & 1 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{0 \cr 0 \cr}\right].$

Since $\displaystyle \det \left[\matrix{3 & 2 \cr 1 & 1 \cr}\right] = 1 \ne 0$ , I know by linear algebra that the matrix equation has only the trivial solution: . This proves that if $(x, y) \in \ker f$ , then , so $\ker f \subset \{(0, 0)\}$ . Since $(0, 0) \in \ker f$ , it follows that $\ker f = \{(0, 0)\}$ .

Hence, f is injective.

Theorem. ( The First Isomorphism Theorem) Let $\phi: G \rightarrow H$ be a group map, and let $\pi: G \rightarrow G/\ker \phi$ be the quotient map. There is an isomorphism $\tilde{\phi}: G/\ker \phi \rightarrow \im \phi$ such that the following diagram commutes:

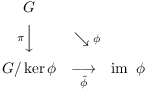
$\def\normalbaselines{\baselineskip20 pt \lineskip3 pt \lineskiplimit3 pt} \def\mapright#1{\smash{ \mathop{\longrightarrow}\limits_{#1}}} \def\mapdown#1{\llap{$\vcenter{\hbox{$\scriptstyle#1$}}$} \Big\downarrow} \def\mapse#1{\searrow \rlap{$\vcenter{\hbox{$\scriptstyle#1$}}$}} \matrix{ G & & \cr \mapdown{\pi} & \mapse{\phi} & \cr G/\ker\phi & \mapright{\tilde\phi} & \im\ \phi \cr }$

Proof. Since $\phi$ maps G onto $\im \phi$ and $\ker \phi \subset \ker \phi$ , the universal property of the quotient yields a map $\tilde{\phi}: G/\ker\phi \rightarrow \im \phi$ such that the diagram above commutes. Since $\phi$ is surjective, so is $\tilde{\phi}$ ; in fact, if $\phi(g) \in \im \phi$ , by commutativity

$\tilde{\phi}(\pi(g)) = \phi(g).$

It remains to show that $\tilde{\phi}$ is injective.

By the previous lemma, it suffices to show that $\ker \tilde{\phi} = \{1\}$ . Since $\tilde{\phi}$ maps out of $G/\ker \phi$ , the "1" here is the identity element of the group $G/\ker \phi$ , which is the subgroup $\ker \phi$ . So I need to show that $\ker \tilde{\phi} = \{\ker \phi\}$ .

However, this follows immediately from commutativity of the diagram. For $g \ker \phi \in \ker \tilde{\phi}$ if and only if $\tilde{\phi}(g \ker \phi) = 1$ . This is equivalent to $\tilde{\phi}(\pi(g)) = 1$ , or $\phi(g) = 1$ , or $g \in \ker \phi$ --- i.e. $\ker \tilde{\phi} = \{\ker \phi\}$ .

Example. ( Using the First Isomorphism Theorem to show two groups are isomorphic) Use the First Isomorphism Theorem to prove that

$\dfrac{\real^*}{\{1, -1\}} \approx \real^+.$

$\real^*$ is the group of nonzero real numbers under multiplication. $\real^+$ is the group of positive real numbers under multiplication. $\{1 , -1\}$ is the group consisting of 1 and -1 under multiplication (it's isomorphic to $\integer_2$ ).

I'll define a group map from $\real^*$ onto $\real^+$ whose kernel is $\{1 , -1\}$ .

Define $\phi: \real^* \to \real^+$ by

$\phi(x) = |x|.$

$\phi$ is a group map:

$\phi(xy) = |xy| = |x||y| = \phi(x)\phi(y).$

If $z \in \real^+$ is a positive real number, then

$\phi(z) = |z| = z.$

Therefore, $\phi$ is surjective: $\im \phi = \real^+$ .

Finally, $\phi$ clearly sends 1 and -1 to the identity $1 \in \real^+$ , and those are the only two elements of $\real^*$ which map to 1. Therefore, $\ker \phi = \{1, -1\}$ .

By the First Isomorphism Theorem,

$\dfrac{\real^*}{\{1, -1\}} = \dfrac{\real^*}{\ker \phi} \approx \im \phi = \real^+.$

Note that I didn't construct a map $\dfrac{\real^*}{\{1, -1\}} \to \real^+$ explicitly; the First Isomorphism Theorem constructs the isomorphism for me.

Example. $\real^2$ is a group under componentwise addition and $\real$ is a group under addition. Let

$H = \left\{x \cdot (\sqrt{5}, -\pi) \Bigm| x \in \real\right\}.$

Prove that $\dfrac{\real^2}{H} \approx \real$ .

Define $f: \real^2 \to \real$ by

$f(x, y) = \pi x + \sqrt{5} y.$

Note that

$f\left(\left[\matrix{x \cr y \cr}\right]\right) = \left[\matrix{\pi & \sqrt{5} \cr}\right] \left[\matrix{x \cr y \cr}\right].$

Since f can be expressed as multiplication by a constant matrix, it's a linear transformation, and hence a group map.

Let $x \cdot (\sqrt{5}, -\pi) \in H$ . Then

$f[x \cdot (\sqrt{5}, -\pi)] = f(\sqrt{5} x, -\pi x) = \pi(\sqrt{5} x) + \sqrt{5}(-\pi x) = 0.$

Therefore, $x \cdot (\sqrt{5}, -\pi) \in \ker f$ , and hence $H \subset \ker f$ .

Let $(x, y) \in \ker f$ . Then

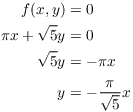
$\eqalign{ f(x, y) & = 0 \cr \pi x + \sqrt{5} y & = 0 \cr \sqrt{5} y & = -\pi x \cr \noalign{\vskip2pt} y & = -\dfrac{\pi}{\sqrt{5}} x \cr}$

Hence,

$(x, y) = \left(x, -\dfrac{\pi}{\sqrt{5}} x\right) = \dfrac{1}{\sqrt{5}} x \cdot (\sqrt{5}, -\pi) \in H.$

Therefore, $\ker f \subset H$ . Hence, $\ker f = H$ .

Let $z \in \real$ . Note that

$f\left(\dfrac{1}{\pi} z, 0\right) = \pi \cdot \dfrac{1}{\pi} z + \sqrt{5} \cdot 0 = z.$

Hence, $\im f = \real$ .

Thus,

$\dfrac{\real^2}{H} = \dfrac{\real^2}{\ker f} \approx \im f = \real.\quad\halmos$

Example. $\integer \times \integer$ is a group under componentwise addition and $\integer$ is a group under addition. Prove that

$\dfrac{\integer \times \integer}{\langle (12, 17) \rangle} \approx \integer.$

Define $f: \integer \times \integer \to \integer$ by

f can be represented by matrix multiplication:

$\left(\left[\matrix{x \cr y \cr}\right]\right) = \left[\matrix{17 & -12 \cr}\right] \left[\matrix{x \cr y \cr}\right].$

Hence, it's a group map.

Let $n (12, 17) = (12 n, 17 n) \in \langle (12, 17) \rangle$ . Then

Thus, $\langle (12, 17) \rangle \subset \ker f$ .

Let $(x, y) \in \ker f$ . Then

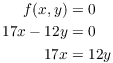
$\eqalign{ f(x, y) & = 0 \cr 17 x - 12 y & = 0 \cr 17 x & = 12 y \cr}$

Now $17 \mid 12 y$ but . By Euclid's lemma, $17 \mid y$ . Say . Then

$17 x = 12 (17 n), \quad\hbox{so}\quad x = 12 n.$

Therefore,

$(x, y) = (12 n, 17 n) = n (12, 17) \in \langle (12, 17) \rangle.$

Thus, $\ker f \subset \langle (12, 17) \rangle$ .

Hence, $\langle (12, 17) \rangle = \ker f$ .

Let $z \in \integer$ . Note that

$1 = (17, -12) = 5 \cdot 17 + 7 \cdot (-12).$

Multiplying by z, I get

Then

This proves that $\im f = \integer$ .

Hence,

$\dfrac{\integer \times \integer}{\langle (12, 17) \rangle} = \dfrac{\integer \times \integer}{\ker f} \approx \im f = \integer.\quad\halmos$

Example. $\real \times \real \times \real$ is a group under componentwise addition. Consider the subgroup

$H = \left\{x \cdot (1, 2, 3) \Bigm| x \in \real\right\}.$

Prove that $\dfrac{\real \times \real \times \real}{H} \approx \real \times \real$ .

( $\real \times \real$ is a group under componentwise addition.)

Define $f: \real \times \real \times \real \to \real \times \real$ by

Note that

$f\left(\left[\matrix{x \cr y \cr z \cr}\right]\right) = \left[\matrix{ -2 & 1 & 0 \cr -3 & 0 & 1 \cr}\right] \left[\matrix{x \cr y \cr z \cr}\right].$

Since f is defined by matrix multiplication, it is a linear transformation. Hence, it's a group map.

Let $x \cdot (1, 2, 3) = (x, 2 x, 3 x) \in H$ . Then

Hence, $(x, 2 x, 3 x) \in \ker f$ , and $H \subset \ker f$ .

Let $(x, y, z) \in \ker f$ . Then

$\eqalign{ f(x, y, z) & = (0, 0) \cr (y - 2 x, z - 3 x) & = (0, 0) \cr}$

Equating the first components, I have , so . Equating the second components, I have , so . Thus,

$(x, y, z) = (x, 2 x, 3 x) \in H.$

Therefore, $\ker f \subset H$ , and so $H = \ker f$ .

Let $(a, b) \in \real \times \real$ . Then

$f(0, a, b) = (a - 2 \cdot 0, b - 3 \cdot 0) = (a, b).$

Hence, $\im f = \real \times \real$ .

Thus,

$\dfrac{\real \times \real \times \real}{H} = \dfrac{\real \times \real \times \real}{\ker f} \approx \im f = \real \times \real.$

The first equality follows from $H = \ker f$ . The isomorphism follows from the First Isomorphism Theorem. The second equality follows from $\im f = \real \times \real$ .

Proposition. If $\phi: G \to H$ is a surjective group map and $K \triangleleft G$ , then $\phi(K) \triangleleft H$ .

Proof. $1 \in K$ , so $1 = \phi(1) \in \phi(K)$ , and $\phi(K) \ne \emptyset$ .

Let $a, b \in K$ , so $\phi(a), \phi(b) \in \phi(K)$ . Then

$\phi(a) \phi(b)^{-1} = \phi(a)\phi(b^{-1}) = \phi(ab^{-1}) \in \phi(K), \hbox{ since } ab^{-1} \in K.$

Therefore, $\phi(K)$ is a subgroup.

(Notice that this does not use the fact that K is normal. Hence, I've actually proved that the image of a subgroup is a subgroup.)

Now let $h \in H$ , $a \in K$ , so $\phi(a) \in \phi(K)$ . I want to show that $h \phi(a) h^{-1} \in \phi(K)$ . Since $\phi$ is surjective, $h = \phi(g)$ for some $g \in G$ . Then

$h \phi(a) h^{-1} = \phi(g) \phi(a) \phi(g)^{-1} = \phi\left(g a g^{-1}\right).$

But $g a g^{-1} \in K$ because K is normal. Hence, $\phi\left(g a g^{-1}\right) \in \phi(K)$ . It follows that $\phi(K)$ is a normal subgroup of H.

Theorem. ( The Second Isomorphism Theorem) Let $K, H \triangleleft G$ , . Then

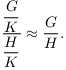
$\dfrac{\dfrac{G}{K}}{\dfrac{H}{K}} \approx \dfrac{G}{H}.$

Proof. I'll use the First Isomorphism Theorem. To do this, I need to define a group map $\dfrac{G}{K} \to \dfrac{G}{H}$ .

To define this group map, I'll use the Universal Property of the Quotient.

The quotient map $\pi: G \to \dfrac{G}{H}$ is a group map. By the lemma preceding the Universal Property of the Quotient, $H = \ker \pi$ . Since $K \subset H$ , it follows that $K \subset \ker \pi$ .

Since $\pi: G \to \dfrac{G}{H}$ is a group map and $K \subset \ker \pi$ , the Universal Property of the Quotient implies that there is a group map $\tilde{\pi}: \dfrac{G}{K} \to \dfrac{G}{H}$ given by

$\tilde{\pi}(g K) = g H.$

If $gH \in \dfrac{G}{H}$ , then $\tilde{\pi}(g K) = gH$ . Therefore, $\tilde{\pi}$ is surjective.

I claim that $\ker \tilde{\pi} = \dfrac{H}{K}$ .

First, if $h K \in \dfrac{H}{K}$ (so $h \in H$ ), then $\tilde{\pi}(h K) = h H = H$ . Since H is the identity in $\dfrac{G}{H}$ , it follows that $h K \in \ker \tilde{\pi}$ .

Conversely, suppose $g K \in \ker \tilde\pi$ , so

$\tilde{\pi}(g K) = H, \quad\hbox{or}\quad g H = H.$

The last equation implies that $g \in H$ , so $gK \in \dfrac{H}{K}$ .

Thus, $\ker \tilde{\pi} = \dfrac{H}{K}$ .

By the First Isomorphism Theorem,

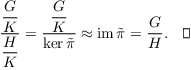
$\dfrac{\dfrac{G}{K}}{\dfrac{H}{K}} = \dfrac{\dfrac{G}{K}}{\ker \tilde{\pi}} \approx \im \tilde{\pi} = \dfrac{G}{H}.\quad\halmos$

There is also a Third Isomorphism Theorem (sometimes called the Modular Isomorphism, or the Noether Isomorphism). It asserts that if and $K \triangleleft G$ , then

$\dfrac{H}{H \cap K} \approx \dfrac{H K}{K}.$

You can prove it using the First Isomorphism Theorem, in a manner similar to that used in the proof of the Second Isomorphism Theorem.

Contact information

Bruce Ikenaga's Home Page