Greatest Common Divisors

Definition. If m and n are integers, not both 0, the greatest common divisor $(m, n)$ of m and n is the largest integer which divides m and n. $(0, 0)$ is undefined. I'll often get lazy and abbreviate "greatest common divisor" to "gcd".

Example. ( Greatest common divisors for small integers) Find by direct computation $(4, 6)$ , $(-6, 15)$ , $(0, 42)$ , and $(24, 25)$ .

The largest integer which divides 4 and 6 is 2:

$$(4, 6) = 2.$$

The largest integer which divides -6 and 15 is 3:

$$(-6, 15) = 3.$$

The largest integer which divides 42 and 0 is 42:

$$(0, 42) = 42.$$

Finally, the largest integer which divides 24 and 25 is 1:

$$(24, 25) = 1.\quad\halmos$$

Here are some easy properties of the greatest common divisor.

Proposition. Let $a, b \in \integer$ , and suppose a and b aren't both 0.

(a) $(a, b) \mid a$ and $(a, b) \mid b$ .

(b) $(a, b)$ exists, and $(a, b) \ge 1$ .

(c) $(a, b) = (b, a)$ .

(d) If $a \ne 0$ , then $(a, 0) = |a|$ .

(e) $(a, b) = (|a|, |b|)$ .

(f) $(a, 1) = 1$ .

Proof. (a) That $(a, b) \mid a$ and $(a, b) \mid b$ follows directly from the definition of $(a, b)$ . (I'm singling this out even though it's easy, because it's a property that is often used.)

(b) On the one hand, the set of common divisors is finite (because a common divisor can't be larger than $|a|$ or $|b|$ ), so it must have a largest element.

Now $1 \mid a$ and $1 \mid b$ , so 1 is a common divisor of a and b. Hence, the greatest common divisor $(a, b)$ must be at least as big as 1 --- that is, $(a, b) \ge 1$ .

(c) The largest integer which divides both a and b is the same as the largest integer which divides both b and a.

(d) $|a| \mid a$ , since $(\pm 1)|a| = a$ , and $|a| \mid 0$ , since $|a| \cdot 0 = 0$ . Thus, $|a|$ is a common divisor of a and 0, so $|a| \le (a, 0)$ .

But $(a, 0) \mid a \mid |a|$ , so $(a, 0) \le |a|$ . Hence, $(a, 0) = |a|$ .

(e) $(a, b)$ divides a, so it divides $|a|$ . Likewise, $(a, b)$ divides $|b|$ . Since $(a, b)$ is a common divisor of $|a|$ and $|b|$ , I have $(a, b) \le (|a|, |b|)$ .

In similar fashion, $(|a|, |b|)$ is a common divisor of a and b, so $(|a|, |b|) \le (a, b)$ .

Therefore, $(a, b) = (|a|, |b|)$ .

(f) $(a, 1) \mid 1$ , but $(a, 1) \ge 1$ . The only positive integer that divides 1 is 1. Hence, $(a, 1) = 1$ .

I'll use the Division Algorithm to derive a method for computing the greatest common divisor of two numbers. The idea is to perform the Division Algorithm repeatedly until you get a remainder of 0. First, I need a lemma which is useful in its own right.

Lemma. If a and b are integers, not both 0, and k is an integer, then

$$(a, b) = (a + k b, b).$$

Proof. If d divides a and b, then d divides $k b$ , so d divides $a + k b$ . Thus, d is a common divisor of $a + k b$ and b.

If d divides $a + k b$ and b, then d divides $k b$ , so d divides $(a + k b) - k b = a$ . Thus, d is a common divisor of a and b.

I've proved that the set of common divisors of a and b is the same as the set of common divisors of $a + k b$ and b. Since the two sets are the same, they must have the same largest element --- that is, $(a, b) = (a + k b, b)$ .

The lemma says that the greatest common divisor of two numbers is not changed if I change one of the numbers by adding or subtracting an integer multiple of the other. This can be useful by itself in determining greatest common divisors.

Example. Prove that if n is an integer, then

$$(2 n^2 + 5 n + 5, n^2 + 2 n + 2) = 1.$$

The idea is to subtract multiples of one number from the other to reduce the powers until I get an expression which is clearly equal to 1.

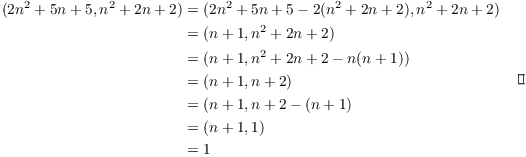
$$\eqalign{ (2 n^2 + 5 n + 5, n^2 + 2 n + 2) & = (2 n^2 + 5 n + 5 - 2(n^2 + 2 n + 2), n^2 + 2 n + 2) \cr & = (n + 1, n^2 + 2 n + 2) \cr & = (n + 1, n^2 + 2 n + 2 - n(n + 1)) \cr & = (n + 1, n + 2) \cr & = (n + 1, n + 2 - (n + 1) \cr & = (n + 1, 1) \cr & = 1 \cr} \quad\halmos$$

Theorem. ( The Euclidean Algorithm) Let $a_0, a_1 \in \integer^+$ , and suppose $a_0 \ge a_1$ . Define $q_1$ , $q_2$ , ... and $a_2$ , $a_3$ , ... by recursively applying the Division Algorithm:

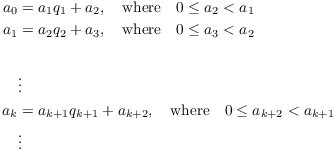
$$\eqalign{ a_0 &= a_1 q_1 + a_2, \quad\hbox{where}\quad 0 \le a_2 < a_1 \cr a_1 &= a_2 q_2 + a_3, \quad\hbox{where}\quad 0 \le a_3 < a_2 \cr \cr &\vdots \cr a_k &= a_{k+1} q_{k+1} + a_{k+2}, \quad\hbox{where}\quad 0 \le a_{k+2} < a_{k+1} \cr &\vdots \cr}$$

Then:

(a) The process will terminate with $a_{n+1} = 0$ for some n.

(b) At the point when the process terminates, $(a_0,a_1) = a_n$ .

Proof. There is no question that I can apply the Division Algorithm as described above, as long as $a_k \ne 0$ .

First, I'll show that the process terminates with $a_{n+1} = 0$ for some n.

Note that $a_1 > a_2 > a_3 > \cdots$ is a decreasing sequence of nonnegative integers. The well-ordering principle implies that this sequence cannot be infinite. Since the only way the process can stop is if a remainder is 0, I must have $a_{n+1} = 0$ for some n.

Suppose $a_{n+1}$ is the first remainder that is 0. I want to show $(a_0,a_1) = a_n$ .

At any stage, I'm starting with $a_k$ and $a_{k+1}$ and producing $q_{k+1}$ and $a_{k+2}$ using the Division Algorithm:

$$a_k = a_{k+1}q_{k+1} + a_{k+2}, \quad\hbox{where}\quad 0 \le a_{k+2} < a_{k+1}.$$

Since $a_{k+2} = a_k - a_{k+1}q_{k+1}$ , the previous lemma implies that

$$(a_k, a_{k+1}) = (a_k - a_{k+1}q_{k+1}, a_{k+1}) = (a_{k+2}, a_{k+1}) = (a_{k+1}, a_{k+2}).$$

This means that

$$(a_0, a_1) = (a_1, a_2) = \cdots = (a_n, a_{n+1}) = (a_n, 0) = a_n.$$

In other words, each step leaves the greatest common divisor of the pair of a's unchanged. Thus, $(a_0,a_1) = a_n$ .

Example. ( Using the Euclidean algorithm to find a greatest common divisor) Use the Euclidean algorithm to compute $(51, 36)$ .

Write

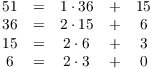
$$\matrix{ 51 & = & 1 \cdot 36 & + & 15 \cr 36 & = & 2 \cdot 15 & + & 6 \cr 15 & = & 2 \cdot 6 & + & 3 \cr 6 & = & 2 \cdot 3 & + & 0 \cr}$$

To save writing --- and to anticipate the setup I'll use for the Extended Euclidean Algorithm later --- I'll arrange the computation in a table:

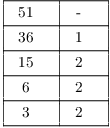
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 51 & & - & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 36 & & 1 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 15 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 6 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & \cr & 3 & & 2 & \cr height2 pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

The greatest common divisor is the last nonzero remainder (3). Hence, $(51, 36) = 3$ .

Definition. If a and b are things, a linear combination of a and b is something of the form $s a + t b$ , where s and t are numbers. (The kind of "number" depends on the context.)

The next result is a key fact about greatest common divisors.

Theorem. ( Extended Euclidean Algorithm) $(a, b)$ is a linear combination of a and b: $(a, b) = s a + t b$ for some integers s and t.

Note: s and t are not unique.

Proof. The proof will actually give an algorithm which constructs a linear combination. It is called a backward recurrence, and it appears in a paper by S. P. Glasby [2]. It will look a little complicated, but you'll see that it's really easy to use in practice.

$(a, b)$ is only defined if at least one of a, b is nonzero. If $a \ne 0$ , $(a, 0) = a$ and $a = 1 \cdot a + 0 \cdot 0$ . This proves the result if one of the numbers is 0, so I may as well assume both are nonzero. Moreover, since $(a, b) = (|a|, |b|)$ , I can assume both numbers are positive.

Suppose $a \ge b$ . Apply the Euclidean Algorithm to $a_0 = a$ and $a_1 = b$ , and suppose that $a_n$ is the last nonzero remainder:

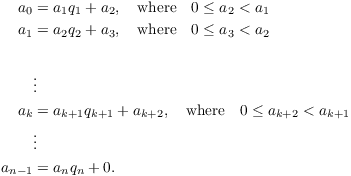
$$\eqalign{ a_0 &= a_1 q_1 + a_2, \quad\hbox{where}\quad 0 \le a_2 < a_1 \cr a_1 &= a_2 q_2 + a_3, \quad\hbox{where}\quad 0 \le a_3 < a_2 \cr \cr &\vdots \cr a_k &= a_{k+1} q_{k+1} + a_{k+2}, \quad\hbox{where}\quad 0 \le a_{k+2} < a_{k+1} \cr &\vdots \cr a_{n-1} &= a_n q_n + 0. \cr}$$

I'm going to define a sequence of numbers $y_n$ , $y_{n-1}$ , ... $y_1$ , $y_0$ . They will be constructed recursively, starting with $y_n$ , $y_{n-1}$ and working downward to $y_0$ . (This is why this is called a backward recurrence.)

Define $y_n = 0$ and $y_{n-1} = 1$ . Then define

$$y_{k-1} = q_k y_k + y_{k+1} \quad\hbox{for}\quad k = n-2, \ldots, 2, 1.$$

Now I claim that

$$(-1)^{n+k+1} a_{k-1} y_k + (-1)^{n+k} a_k y_{k-1} = a_n \quad\hbox{for}\quad 1 \le k \le n.$$

I will prove this by downward induction, starting with $k = n$ and working downward to $k = 1$ .

For $k = n$ , I have

$$(-1)^{2 n + 1} a_{n-1} y_n + (-1)^{2 n} a_n y_{n-1} = -a_{n-1} y_n + a_n y_{n-1} = -a_{n-1} \cdot 0 + a_n \cdot 1 = a_n.$$

The result holds for $k = n$ .

Next, suppose $1 < k < n$ . Suppose the result holds for $k + 1$ , i.e.

$$(-1)^{n+k+2} a_k y_{k+1} + (-1)^{n+k+1} a_{k+1}y_k = a_n.$$

I want to prove the result for k. Substitute $y_{k+1} = y_{k-1} - q_k y_k$ in the preceding equation and simplify:

$$a_n = (-1)^{n+k+2} a_k y_{k+1} + (-1)^{n+k+1} a_{k+1} y_k = (-1)^{n+k+2} a_k (y_{k-1} - q_k y_k) + (-1)^{n+k+1} a_{k+1} y_k =$$

$$(-1)^{n+k} a_k (y_{k-1} - q_k y_k) + (-1)^{n+k+1} a_{k+1} y_k = (-1)^{n+k} a_k y_{k-1} + (-1)^{n+k+1} a_k q_k y_k + (-1)^{n+k+1} a_{k+1} y_k =$$

$$(-1)^{n+k} a_k y_{k-1} + (a_k q_k + a_{k+1})(-1)^{n+k+1} y_k = (-1)^{n+k} a_k y_{k-1} + (-1)^{n+k+1} a_{k-1} y_k.$$

This proves the result for k, so the result holds for $1 \le k \le n$ , by downward induction.

In particular, for $k = 1$ , the result says

$$a_n = (-1)^{n+1} a_1 y_0 + (-1)^{n+2} a_0 y_1 = (-1)^{n+1} a_1 y_0 + (-1)^n a_0 y_1 = \left((-1)^n y_1\right) a_0 + \left((-1)^{n+1} y_0\right) a_1.$$

Since $a_n = (a_0, a_1)$ , I've expressed $(a_0, a_1)$ as a linear combination of $a_0$ and $a_1$ .

Remark. There are many algorithms (like the one in the proof) which produce a linear combination. This one is pretty good for small computations which you're doing by hand.

One drawback of this algorithm is that you need to know all of the quotients (the q's) in order to work backwards to get the linear combination. This isn't bad for small numbers, but if you're using large numbers on a computer, you'll need to store all the intermediate results. There are algorithms which are better if you're doing large computations on a computer (see [1], page 300).

It's difficult to overemphasize the importance of this result! It has many applications --- from proving results about greatest common divisors, to solving Diophantine equations. I'll give some examples which illustrate the result, then discuss how you use the algorithm in the theorem.

Before I give examples of the algorithm, I'll look at some other ways of finding a linear combination.

Definition. Let $a, b \in \integer$ . a and b are relatively prime if $(a, b) = 1$ .

Example. ( A linear combination for a greatest common divisor) Show that 12 and 25 are relatively prime. Write their greatest common divisor as as linear combination with integer coefficients of 12 and 25. In some cases, the numbers are nice enough that you can figure out a linear combination by trial and error.

In this case, it's clear that $12 = 2^2 \cdot 3$ and $25 = 5^2$ are relatively prime. So $(12, 25) = 1$ ; to get a linear combination, I need multiples of 12 and 25 which differ by 1. Here's an easy one:

$$(-2) \cdot 2 + 1 \cdot 25 = 1.$$

Note that $23 \cdot 12 + (-11) \cdot 25 = 1$ , so the linear combination is not unique.

Example. ( Finding a linear combination by algebra) Use the Division Algorithm computations in the Euclidean algorithm to find an integer linear combination of 51 and 36 that is equal to $(51, 36) = 3$ .

It's possible --- but tedious --- to use the computations in the Euclidean algorithm to find linear combinations. For $(51, 36)$ , I have

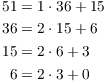
$$\eqalign{ 51 & = 1 \cdot 36 + 15 \cr 36 & = 2 \cdot 15 + 6 \cr 15 & = 2 \cdot 6 + 3 \cr 6 & = 2 \cdot 3 + 0 \cr}$$

The third equation says $3 = 15 - 2 \cdot 6$ .

By the second equation, $6 = 36 - 2 \cdot 15$ , so

$$3 = 15 - 2 \cdot (36 - 2 \cdot 15) = 5 \cdot 15 - 2 \cdot 36.$$

The first equation says $15 = 51 - 36$ , so

$$3 = 5 \cdot (51 - 36) - 2 \cdot 36 = 5 \cdot 51 - 7 \cdot 36.$$

I've expressed the greatest common divisor 3 as a linear combination of the original numbers 51 and 36.

I don't recommend this approach, since the proof of the Extended Euclidean Algorithm gives a method which is much easier and less error-prone.

Example. ( Finding a linear combination using the backward recursion) Find $(187, 102)$ and express it as a linear combination with integer coefficients of 187 and 102.

In this example, I'll show how you can use the bakcward recursion to obtain a linear combination. I'll arrange the computations in the form of a table; the table is simply an extension of the table I used for the Euclidean algorithm.

In this example only, I'm labelling the columns with the variable names a, q, and y from the proof so you can see the correspondence. Normally, I'll omit them.

Here's how you start:

$$\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-0.eps}}$$

(You can save a step by putting the larger number first.)

The a and q columns are filled in using the Euclidean algorith, i.e. by successive division: Divide the next-to-the-last a by the last a. The quotient goes into the q-column, and the remainder goes into the a-column.

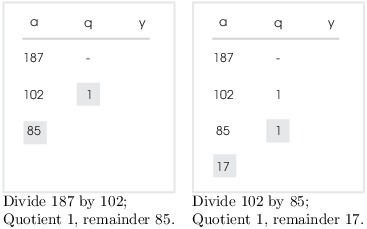
$$\matrix{\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-1.eps}} & \hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-2.eps}} \cr \vbox{\hbox{Divide 187 by 102;} \hbox{Quotient 1, remainder 85.}} & \vbox{\hbox{Divide 102 by 85;} \hbox{Quotient 1, remainder 17.}} \cr}$$

When the division comes out evenly, you stop adding rows to the table. In this case, 85 divided by 17 is 5, and the remainder is 0.

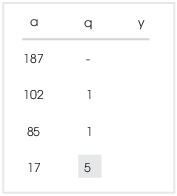
$$\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-3.eps}}$$

The last entry in the a-column is the greatest common divisor. Thus, $(187, 102) = 17$ .

Having filled in the a and q columns, you now fill in the y-column from bottom to top. You always start in the same way: The last y is always 0 and the next-to-the-last y is always 1:

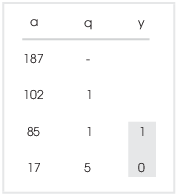
$$\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-4.eps}}$$

Then, working from bottom to top, fill in the y's using the rule

$$(\hbox{next y}) = (\hbox{last q}) \cdot (\hbox{last y}) + (\hbox{next-to-last y}).$$

This comes from the recursion formula in the Extended Euclidean Algorithm Theorem:

$$a_k = a_{k+1} q_{k+1} + a_{k+2}.$$

It's probably easier to show than it is to explain:

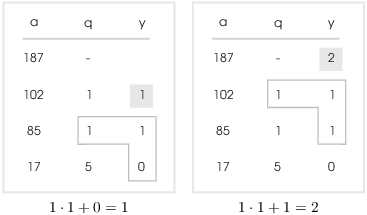
$$\matrix{\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-5.eps}} & \hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-6.eps}} \cr 1 \cdot 1 + 0 = 1 & 1 \cdot 1 + 1 = 2 \cr}$$

To get the linear combination, form the products of the top two a's and y's diagonally and subtract one from the other:

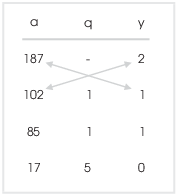
$$\hbox{\epsfysize=1.75 in \epsffile{greatest-common-divisors-7.eps}}$$

Thus,

$$17 = (187, 102) = (2)(102) - (1)(187).$$

How do you know the order for the subtraction? The proof gives a formula, but the easiest thing is to pick one of the two ways, then fix it if it isn't right. If you subtract "the wrong way", you'll get a negative number. For example,

$$(1)(187) - (2)(102) = -17.$$

Since I know the greatest common divisor should be 17 --- it's the last number in the a-column --- I just multiply this equation by -1:

$$(-1)(187) + (2)(102) = 17.$$

This way, you don't need to memorize the exact formula.

Example. ( Finding a linear combination using the backward recursion) Compute $(246, 194)$ and express it as an integer linear combination of 246 and 194.

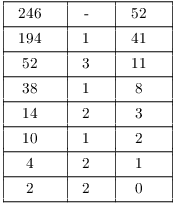
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 246 & & - & & 52 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 194 & & 1 & & 41 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 52 & & 3 & & 11 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 38 & & 1 & & 8 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 14 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 10 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 4 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$2 = (246, 194) = 52 \cdot 194 - 41 \cdot 246.\quad\halmos$$

Example. ( The converse of the linear combination result) Give specific numbers a, b, m, n and d such that

$$a m + b n = d \quad\hbox{but}\quad (m, n) \ne d.$$

The converse of the linear combination result is not always true. That is, if $s a + t b = z$ for some numbers s and t, it's not necessarily true that $z = (a, b)$ .

For example, $15 = 1 \cdot 51 + (-1) \cdot 36$ . But $(51, 36) = 3 \ne 15$ .

There's an important situation in which the linear combination result does work backwards: namely, when the greatest common divisor is 1. The next result makes this precise, and also shows how you can use the linear combination rule to prove results about greatest common divisors.

Proposition. Let $a, b \in \integer$ . Then $(a, b) = 1$ if and only if

$$s a + t b = 1 \quad\hbox{for some}\quad s, t \in \integer.$$

Proof. The greatest common divisor of a and b can be written as a linear combination of a and b. Therefore, if $(a, b) = 1$ , then

$$1 = (a, b) = s a + t b \quad\hbox{for some}\quad s, t \in \integer.$$

Conversely, suppose that $s a + t b = 1$ for some $s, t \in \integer$ . $(a, b)$ divides a and $(a, b)$ divides b, so $(a, b)$ divides $s a + t b = 1$ . But $(a, b)$ is a positive integer, and the only positive integer that divides 1 is 1. Therefore, $(a, b) = 1$ .

Example. ( Using a linear combination to prove relative primality) Prove that if k is any integer, then the fraction $\dfrac{10 k + 6}{12 k + 7}$ is in lowest terms.

For example, if $k = 11$ , the fraction is $\dfrac{116}{139}$ , which is in lowest terms.

A fraction is in lowest terms if the numerator and denominator are relatively prime. So I want to show that $10 k + 6$ and $12 k + 7$ are relatively prime.

I'll use the previous result, noting that

$$6 (10 k + 6) + (-5) (12 k + 7) = 1.$$

I found the coefficients by playing with numbers, trying to make the k-terms cancel.

Since a linear combination of $10 k + 6$ and $12 k + 7$ equals 1, the last proposition shows that $10 k + 6$ and $12 k + 7$ are relatively prime.

The linear combination rule is often useful in proofs involving greatest common divisors. If you're proving a result about a greatest common divisor, consider expressing the greatest common divisor as a linear combination of the two numbers.

Proposition. Let a and b be integers, not both 0. If $c \mid a$ and $c \mid b$ , then $c \mid (a, b)$ .

Proof.$(a, b)$ is a linear combination of a and b, so

$$(a, b) = s a + t b \quad\hbox{for some}\quad s, t \in \integer.$$

Now $c \mid a$ and $c \mid b$ , so $c \mid s a + t b = (a, b)$ .

$(a, b)$ was defined to be the greatest common divisor of a and b, in the sense that it was the largest common divisor of a and b. The last lemma shows that you can take greatest in a different sense --- namely, that $(a, b)$ must be divisible by any other common divisor of a and b.

Example. ( Using the linear combination result to prove a greatest common divisor property) Prove that if $(a, b) = 1$ and $k > 0$ , then $(k a, k b) = k$ .

Since $(a, b) = 1$ ,

$$m a + n b = 1 \quad\hbox{for some}\quad m, n \in \integer.$$

Multiplying by k, I get

$$k m a + k n b = k.$$

$(k a, k b) \mid k a$ and $(k a, k b) \mid k b$ , so $(k a, k b) \mid k m a + k n b = k$ .

On the other hand, $k \mid k a$ and $k \mid k b$ , so $k \mid (k a, k b)$ .

Since k and $(k a, k b)$ are positive integers, $(k a, k b) = k$ .

[1] Alfred Aho, John Hopcroft, and Jeffrey Ullman, The Design and Analysis of Computer Algorithms. Reading, Massachusetts: Addison-Wesley Publishing Company, 1974.

[2] S. P. Glasby, Extended Euclid's algorithm via backward recurrence relations, Mathematics Magazine, 72(3)(1999), 228--230.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga