Group Maps Between Finite Cyclic Groups

Group maps $\integer_m \to \integer_n$ are determined by the image of $1 \in \integer_m$ : The image is an element whose order divides $(m, n)$ , and all such elements are the image of such a group map.

Theorem.

(a) If $f: \integer_m \to \integer_n$ is a group map, then $\ord f(1) \mid (m, n)$ .

(b) If $p \in \integer_n$ satisfies $\ord p \mid (m, n)$ , then there is a group map $f: \integer_m \to \integer_n$ such that $f(1) = p$ .

Proof. (a) Suppose $f: \integer_m \to \integer_n$ is a group map. Now $m \cdot 1 = 0$ in $\integer_m$ , so

$$m \cdot f(1) = f(m \cdot 1) = f(0) = 0.$$

This shows that $\ord f(1) \mid m$ .

Since $f(1) \in \integer_n$ , I have $\ord f(1) \mid n$ .

Hence, $\ord f(1) \mid (m, n)$ .

(b) Let $p \in \integer_n$ , and suppose $d = \ord p \mid (m, n)$ . Define $g: \integer \to \integer_n$ by

$$g(x) = p x.$$

Since $d \mid m$ , I have $m = j d$ for some $j \in \integer$ .

Now

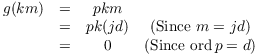
$$\matrix{ g(k m) & = & p k m & \cr & = & p k (j d) & (\hbox{Since $m = j d$}) \cr & = & 0 & (\hbox{Since $\ord p = d$}) \cr}$$

Since g sends $m \integer$ to 0, the Universal Property of the Quotient produces a (unique) group map $\tilde{g}: \integer_m \to \integer_n$ defined by

$$\tilde{g}(x) = p x.$$

Then $\tilde{g}(1) = p$ , and $\tilde{g}$ is the desired group map.

Corollary. The number of group maps $\integer_m \to \integer_n$ is $(m, n)$ .

Proof. The number of elements of order d in a cyclic group is $\phi(d)$ (where $\phi$ denotes the Euler $\phi$ -function). The divisor sum of the Euler $\phi$ -function is the identity:

$$\sum_{d \mid k} \phi(d) = k.$$

So the number of elements whose orders divide $(m, n)$ is $(m, n)$ , and the theorem shows that each such element gives rise to a group map $\integer_m \to \integer_n$ .

Example. (a) Enumerate the group maps $\integer_{18} \to \integer_{30}$ .

(b) Show by direct computation that $f: \integer_{18} \to \integer_{30}$ given by $f(x) = 14 x$ is not a group map.

(a) Since $(18, 30) = 6$ , there are 6 such maps by the Corollary. They are determined by sending $1 \in \integer_{18}$ to an element whose order divides 6.

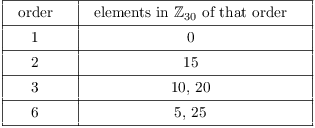
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & order & & elements in $\integer_{30}$ of that order & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & 0 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & 15 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 3 & & 10, 20 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 6 & & 5, 25 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, the possible group maps $f: \integer_{18} \to \integer_{30}$ have

$$f(1) = 0, \quad f(1) = 15, \quad f(1) = 10, \quad f(1) = 20, \quad f(1) = 5, \quad f(1) = 25.$$

For example, the group map

$$f(x) = 20 x \quad\hbox{has}\quad f(1) = 20.$$

It is easy to determine the kernel and the image. The image is the unique subgroup of $\integer_{30}$ of order 3, so

$$\im f = \{0, 10, 20\}.$$

By the First Isomorphism Theorem, the kernel must have order $\dfrac{18}{3} = 6$ . The unique subgroup of $\integer_{18}$ of order 6 is

$$\ker f = \{0, 3, 6, 9, 12, 15\}.$$

(b) Consider the function $f: \integer_{18} \to \integer_{30}$ given by $f(x) = 14 x$ .Then

$$f(3 + 15) = f(0) = 0, \quad\hbox{but}\quad f(3) + f(15) = 12 + 0 = 12.$$

Therefore, $f(3 + 15) \ne f(3) + f(15)$ , so f is not a group map.

Contact information

Bruce Ikenaga's Home Page

Copyright 2016 by Bruce Ikenaga