Ideals and Subrings

A subgroup of a group is a subset of the group which is a group in its own right, using the operation it inherits from its parent group. Likewise, a subring of a ring is a subset of the ring which is a ring in its own right, using the addition and multiplication it inherits from its parent ring.

Definition. Let R be a ring. A subring is a subset $S \subset R$ such that:

(a) S is closed under addition: If $a, b \in S$ , then $a + b \in S$ .

(b) The zero element of R is in S: $0 \in S$ .

(c) S is closed under additive inverses: If $a \in S$ , then $-a \in S$ .

(d) S is closed under multiplication: If $a, b \in S$ , then $a b \in S$ .

It turns out to be useful to consider certain other kinds of "subobjects" of rings: Ideals. I'll use ideals to construct quotient rings, which just as I used normal subgroups to construct quotient groups.

Definition. Let R be a ring. An ideal S of R is a subset $S \subset R$ such that:

(a) S is closed under addition: If $a, b \in S$ , then $a + b \in S$ .

(b) The zero element of R is in S: $0 \in S$ .

(c) S is closed under additive inverses: If $a \in S$ , then $-a \in S$ .

(d) If $r \in R$ and $x \in S$ , then $r x \in S$ and $x r \in S$ . In other words, S is closed under multiplication (on either side) by arbitrary ring elements.

What's the difference between a subring and an ideal? A subring must be closed under multiplication of elements in the subring. An ideal must be closed under multiplication of an element in the ideal by any element in the ring.

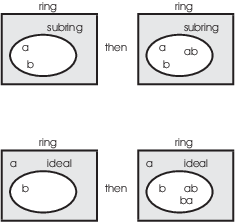
$$\hbox{\epsfysize=2 in \epsffile{ideals-and-subrings-1.eps}}$$

Since the ideal definition requires more multiplicative closure than the subring definition, every ideal is a subring. The converse is false, as I'll show by example below.

In the course of attempting to prove Fermat's Last Theorem, mathematicians were led to introduce rings in which unique factorization failed --- that is, it might be possible to factor a ring element into primes in more than one way. They were led to introduce ideal numbers (essentially what are now called ideals) in an attempt to restore unique factorization.

What I've defined above is usually called a two-sided ideal. If I only require that $r x \in S$ for $r \in R$ and $x \in S$ , I get left ideals. Likewise, if I only require that $x r \in S$ for $r \in R$ and $x \in S$ , I get right ideals.

From now on, if I just say "ideal", I will mean a two-sided ideal.

If R is commutative, then $r b = b r$ , so you only need to check that one of $r b$ , $b r$ , is in S. In the commutative case, there's no difference between left ideals, right ideals, and two-sided ideals.

Lemma. Let R be a ring. Then R and $\{0\}$ are ideals.

Proof. R is a group under addition, and as such I've already proved that R (the whole group) and $\{0\}$ (the set consisting of the identity) are subgroups of R. Thus, they are both closed under addition, contain 0, and are closed under taking additive inverses. I only have to verify the fourth ideal axiom in each case.

For R, if $x \in R$ and $r \in R$ , then $x r, r x \in R$ , because R is closed under multiplication (being the whole ring!). Therefore, R is an ideal.

For $\{0\}$ , take $0 \in \{0\}$ --- what other choice do you have? --- and $r \in R$ . Then

$$r \cdot 0 = 0 \in \{0\} \quad\hbox{and}\quad 0 \cdot r = 0 \in \{0\}.$$

Therefore, $\{0\}$ is an ideal.

Definition. Let R be a ring. A proper ideal is an ideal other than R; a nontrivial ideal is an ideal other than $\{0\}$ .

Example. ( The integers as a subset of the reals) Show that $\integer$ is a subring of $\real$ , but not an ideal.

$\integer$ is a subring of $\real$ : It contains 0, is closed under taking additive inverses, and is closed under addition and multiplication. With regard to multiplication, note that the product of two integers is an integer.

However, $\integer$ is not an ideal in $\real$ . For example, $\sqrt{2} \in \real$ and $3 \in \integer$ , but $\sqrt{2} \cdot 3 \notin \integer$ .

Example. ( An ideal in the ring of integers) Show that the subset $n \integer$ is an ideal in $\integer$ for $n \in \integer$ .

We already know that $n \integer$ is a subgroup of $\integer$ under addition. So I just need to check closure under multiplication.

Let $k \in \integer$ and let $n x \in n \integer$ , where $x \in \integer$ . Then

$$k \cdot (n x) = n (k x) \in n \integer.$$

Therefore, $n \integer$ is an ideal.

Example. ( An ideal in a product ring) In the ring $\integer_4 \times \integer_4$ , consider the subset

$$I = \{(0,0), (1,1), (2,2), (3,3)\}.$$

Show that I is a subring, but not an ideal.

It's easy to check that I is a subring of $\integer_4 \times \integer_4$ . First, I contains the additive identity $(0, 0)$ .

Next, a typical element of I has the form $(n, n)$ . The additive inverse is

$$-(n, n) = (-n, -n) = (4 - n, 4 - n) \in I.$$

If you add two elements of I, you get an element of I:

$$(a, a) + (b, b) = (a + b, a + b).$$

(Of course, you'll reduce $a + b$ mod 4, but the two components remain the same.)

Finally, if you multiply two elements of I, you get an element of I:

$$(a, a) (b, b) = (a b, a b).$$

However, I is not an ideal; for example, $(2, 2) \in I$ , but

$$(3, 0) \cdot (2, 2) = (2, 0) \notin I.$$

In other words, I is closed under multiplication of elements inside I, but not closed under multiplication by an element from outside I.

Definition. Let R be a commutative ring, and let $a \in R$ . The principal ideal generated by a is

$$\langle a \rangle = \{r a \mid r \in R\}.$$

For example, in the ring of polynomials with real coefficients $\real[x]$ , this is the principal ideal generated by $x^2 + 4$ :

$$\langle x^2 + 4 \rangle = \{(x^2 + 4)\cdot f(x) \mid f(x) \in \real[x]\}.$$

It's the set consisting of all multiples of $x^2 + 4$ . For example, here are some elements of $\langle x^2 + 4 \rangle$ :

$$(2 x + 5)\cdot (x^2 + 4), \quad (-\pi x^{50} + \sqrt{2})\cdot (x^2 + 4), \quad 0 = 0\cdot (x^2 + 4).$$

We'd better check that the principal ideal really is an ideal!

Lemma. Let R be a commutative ring, and let $a \in R$ . Then $\langle a \rangle$ is a two-sided ideal in R.

Proof. First, $0 = 0 \cdot a \in \langle a \rangle$ .

If $r a \in \langle a \rangle$ , then $-(ra) = (-r)a \in \langle a \rangle$ .

Finally, if $r a, s a \in \langle a \rangle$ , then $r a + s a = (r + s) a \in \langle a \rangle$ .

Thus, $\langle a \rangle$ is an additive subgroup of R.

If $r a \in \langle a \rangle$ and $s \in R$ , then

$$s (r a) = (s r) a \in \langle a \rangle \quad\hbox{and}\quad (r a) s = (r s) a \in \langle a \rangle.$$

Therefore, $\langle a \rangle$ is a two-sided ideal.

Definition. Let $I_1$ , ..., $I_n$ be ideals in a ring R. The ideal sum is

$$\sum_{k=1}^n I_k = \{x_1 + \cdots + x_n \mid x_k \in I_k\}.$$

Definition. Let I and J be ideals in a ring R. The ideal product is

$$I J = \{x_1 y_1 + \cdots + x_ny_n \mid x_i \in I, y_i \in J\}.$$

Thus, $I J$ consists of all finite sums of products $xy$ , $x \in I$ , $y \in J$ .

Proposition. Let R be a ring.

(a) Suppose R has an identity and I is an ideal. If $1 \in I$ , then $I = R$ .

(b) The intersection $I \cap J$ of (left, right, two-sided) ideals I and J is a (left, right, two-sided) ideal.

(c) If $I_1$ , ..., $I_n$ are (left, right, two-sided) ideals, the ideal sum is a (left, right, two-sided) ideal.

(d) If I and J are (left, right, two-sided) ideals, the ideal product is a (left, right, two-sided) ideal.

Proof. I'll prove the first statement by way of example. Let I be an ideal in a ring with 1. $I \subset R$ , so I need to prove $R \subset I$ . Let $r \in R$ . Now $1 \in I$ , so by the definition of an ideal, $r = r\cdot 1 \in I$ . Therefore, $R \subset I$ , so $R = I$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga