Integral Domains and Fields

Definition. (a) Let R be a commutative ring. A zero divisor is a nonzero element $a \in R$ such that $a b = 0$ for some nonzero $b \in R$ .

(b) A commutative ring with 1 having no zero divisors is an integral domain.

The most familiar integral domain is $\integer$ . It's a commutative ring with identity. If $a, b \in \integer$ and $a b = 0$ , then at least one of a or b is 0.

Definition. (a) Let R be a ring with identity, and let $a \in R$ . A multiplicative inverse of a is an element $a^{-1} \in R$ such that

$$a \cdot a^{-1} = 1 \quad\hbox{and}\quad a^{-1} \cdot a = 1.$$

An element which has a multiplicative inverse is called a unit.

Definition. (a) A ring with identity in which every nonzero element has a multiplicative inverse is called a division ring.

(b) A commutative ring with identity in which every nonzero element has a multiplicative inverse is called a field.

$\rational$ , $\real$ , and $\complex$ are all fields. $\quaternion$ is an example of a division ring which is not a field --- it isn't commutative, since (for example) $i j = k$ but $j i = -k$ .

Example. ( Units and zero divisors in the integers mod n) (a) What are the units in $\integer_n$ ?

(b) List the units and zero divisors in $\integer_{12}$

(a) The units in $\integer_n$ are the elements of $U_n$ ; that is, the elements of $\integer_n$ which are relatively prime to n.

Thus, in $\integer_{12}$ , the elements 1, 5, 7, and 11 are units. For example, $7^{-1} = 7$ .

The zero divisors in $\integer_{12}$ are 2, 3, 4, 6, 8, 9, and 10. For example $2\cdot 6 = 0$ , even though 2 and 6 are nonzero.

Example. ( The units in a matrix ring) What are the units in $M(2, \real)$ ?

The units in $M(2, \real)$ are the invertible matrices --- i.e. the elements of $GL(2, \real)$ .

Example. ( A ring of functions which is not a domain) Show that $C[0,1]$ is not an integral domain.

Let

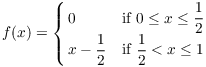
$$f(x) = \cases{ 0 & if $0 \le x \le \dfrac{1}{2}$ \cr x - \dfrac{1}{2} & if $\dfrac{1}{2} < x \le 1$ \cr}$$

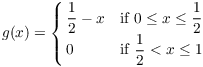
$$g(x) = \cases{ \dfrac{1}{2} - x & if $0 \le x \le \dfrac{1}{2}$ \cr 0 & if $\dfrac{1}{2} < x \le 1$ \cr}$$

Then $f, g \ne 0$ , but $f g = 0$ .

Lemma. ( Cancellation) Let R be a commutative ring with 1. Then R is an integral domain if and only if for all $r, s, t \in R$ , $rs = rt$ and $r \ne 0$ implies $s = t$ .

In other words, you can "cancel" nonzero factors in an integral domain. Note that this is not the same as division, which is multiplication by a multiplicative inverse.

Proof. Suppose R is a domain. Let $r, s, t \in R$ , where $r \ne 0$ , and suppose $rs = rt$ . Then $rs - rt = 0$ , so $r(s - t) = 0$ . Since $r \ne 0$ and since R has no zero divisors, $s - t = 0$ . Therefore, $s = t$ .

Conversely, suppose for all $r, s, t \in R$ , $rs = rt$ and $r \ne 0$ implies $s = t$ . I will show that R has no zero divisors. Suppose $ab = 0$ , where $a \ne 0$ . Now $ab = 0 = a \cdot 0$ , and by cancellation, $b = 0$ . This shows that R has no zero divisors, so R is a domain.

Example. ( Domains and solving by factoring) Show that $x^2 + 3 x - 4 \in \integer_{12}[x]$ has 4 roots.

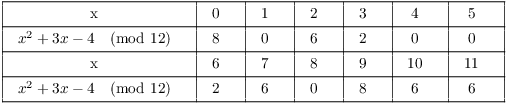
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + 3 x - 4 \pmod{12}$ & & 8 & & 0 & & 6 & & 2 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 6 & & 7 & & 8 & & 9 & & 10 & & 11 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + 3 x - 4 \pmod{12}$ & & 2 & & 6 & & 0 & & 8 & & 6 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, a polynomial of degree n can have more than n roots in a ring. The problem is that $\integer_{12}$ is not a domain: $(x + 4)(x - 1) = 0$ does not imply one of the factors must be zero.

Remark. Here is a picture which shows how the various types of rings are related:

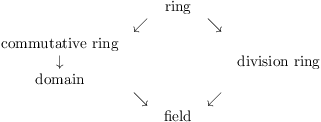
$$\matrix{ & & \hbox{ring} & & \cr & \swarrow & & \searrow & \cr \hbox{commutative ring} & & & & \cr \downarrow & & & & \hbox{division ring} \cr \hbox{domain} & & & & \cr & \searrow & & \swarrow & \cr & & \hbox{field} & & \cr}$$

Thus, a field is a special case of a division ring, just as a division ring is a special case of a ring.

The objects of mathematics are primarily built up from sets by adding axioms to make more complicated structures. For instance, a group is a set with one binary operation satisfying certain axioms. A ring is a set with two binary operations, satisfying certain axioms. You get special kinds of rings by adding axioms to the basic ring definition.

There are many advantages to doing things this way. For one, if you prove something about a simple structure, you know the result will be true about more complicated structures which are built from the simple structure. For another, by using the smallest number of axioms to prove results, you get a deeper understanding of why the result is true.

Lemma. Fields are integral domains.

Proof. Let F be a field. I must show that F has no zero divisors. Suppose $a b = 0$ and $a \ne 0$ . Then a has an inverse $a^{-1}$ , so $a^{-1} a b = a^{-1} \cdot 0$ , or $b = 0$ . Therefore, F has no zero divisors, and F is a domain.

Lemma. If R is a field, the only ideals are $\{0\}$ and R.

Proof. Let R be a field, and let $I \subset R$ be an ideal. Assume $I \ne \{0\}$ , and find $x \ne 0$ in I. Since R is a field, x is invertible; since I is an ideal, $1 = x^{-1} \cdot x \in I$ . Therefore, $I = R$ .

Example. ( A field which extends the rationals) Consider

$$\rational[\sqrt{2}] = \{a + b\sqrt{2} \mid a, b \in \rational\}.$$

Use the operations inherited from the reals. Show that every nonzero element has a multiplicative inverse (so $\rational[\sqrt{2}]$ is a field).

This is clearly a commutative ring. To show that it's a field, suppose $a + b\sqrt{2} \ne 0$ . Then multiplying top and bottom by the conjugate, I have

$$\dfrac{1}{a + b \sqrt{2}} = \dfrac{a - b \sqrt{2}}{a^2 - 2 b^2}.$$

I must show that $a^2 - 2 b^2 \ne 0$ .

If $a = 0$ and $b \ne 0$ or if $a \ne 0$ and $b = 0$ , then $a^2 - 2 b^2 \ne 0$ . Since $a + b \sqrt{2} \ne 0$ , the only other possibility is $a, b \ne 0$ .

Thus, $a^2 = 2 b^2$ with $a, b \ne 0$ . Clearing denominators if necessary, I may assume that a and b are integers --- in fact, positive integers, thanks to the squares. Now 2 divides $2 b^2$ , so $2 \mid a^2$ . This forces $2 \mid a$ , so $a = 2 c$ for some integer c. Plugging in gives $4 c^2 = 2 b^2$ , or $2 c^2 = b^2$ .

Repeat the argument: $2 \mid b^2$ , so $2 \mid b$ , so $b = 2 d$ . Plugging in gives $2 c^2 = 4 d^2$ , or $c^2 = 2 d^2$ .

I can continue this process indefinitely. Notice that $a > c > \ldots$ and $b > d > \ldots$ . This yields infinite descending sequences of positive integers, contradicting well-ordering. Therefore, $a^2 - 2 b^2 \ne 0$ . (This is called an argument by infinite descent.)

It follows that every nonzero element of $\rational[\sqrt{2}]$ is invertible, so $\rational[\sqrt{2}]$ is a field.

Proposition. A finite integral domain is a field.

Proof. Let R be a finite domain. Say

$$R = \{r_1, r_2, \ldots, r_n\}.$$

I must show that nonzero elements are invertible. Let $r \in R$ , $r \ne 0$ .

Consider the products $r r_1, r r_2, \ldots, r r_n$ . If $r r_i = r r_j$ , then $r_i = r_j$ by cancellation. Therefore, the $r r_i$ are distinct. Since there are n of them, they must be exactly all the elements of R:

$$R = \{r r_1, r r_2, \ldots, r r_n\}.$$

Then $1 \in R$ equals $r r_i$ for some i, so r is invertible.

For the proposition that follows, I need the following result on greatest common divisors.

Proposition. $m \in \integer_n$ is a zero divisor if and only if $(m, n) \ne 1$ .

Proof. First, I'll show that if $(m, n) = 1$ , then m is not a zero divisor. Suppose $(m, n) = 1$ , so $a m + b n = 1$ for some $a, b \in \integer$ . Reducing the equation mod n, $a'm = 1$ for some $a' \in \integer_n$ , where $a = a'$ mod n.

Now suppose $k \in \integer_n$ and $m k = 0$ . Then

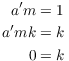
$$\eqalign{ a' m & = 1 \cr a' m k & = k \cr 0 & = k \cr}$$

Therefore, m is not a zero divisor.

Conversely, suppose that $(m, n) = k > 1$ . Say $n = k a$ , where $1 < a < n$ . In particular, I may regard a as a nonzero element of $\integer_n$ .

The order of m in $\integer_n$ is $\dfrac{n}{(m, n)} = \dfrac{n}{k} = a$ . Thus, $m a = 0$ in $\integer_n$ , and m is a zero divisor.

Example. ( Zero divisors in the integers mod n) (a) Find the zero divisors in $\integer_{15}$ .

(b) Find the zero divisors in $\integer_7$ .

(a) The zero divisors are those elements in $\{1, 2, \ldots, 14\}$ which are not relatively prime to 15:

$$3, 5, 6, 9, 10, 12.$$

For example, $5 \cdot 12 = 0 \in \integer_{15}$ shows directly that 5 and 12 are zero divisors.

(b) Since 7 is prime, all the elements in $\{1, 2, 3, 4, 5, 6\}$ are relatively prime to 7. There are no zero divisors in $\integer_7$ . In fact, $\integer_7$ is an integral domain; since it's finite, it's also a field by an earlier result.

Example. List the units and zero divisors in $\integer_4 \times \integer_2$ .

The units are $(1, 1)$ and $(3, 1)$ :

$$(1, 1) \cdot (1, 1) = (1, 1) \quad\hbox{and}\quad (3, 1) \cdot (3, 1) = (1, 1).$$

The zero divisors are

$$(1, 0), (2, 0), (3, 0), (2, 1), (0, 1).$$

To see this, note that

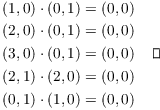
$$\eqalign{ (1, 0) \cdot (0, 1) & = (0, 0) \cr (2, 0) \cdot (0, 1) & = (0, 0) \cr (3, 0) \cdot (0, 1) & = (0, 0) \cr (2, 1) \cdot (2, 0) & = (0, 0) \cr (0, 1) \cdot (1, 0) & = (0, 0) \cr} \quad\halmos$$

Proposition. $\integer_n$ is a field if and only if n is prime.

Proof. If n is composite, I may find $a, b$ such that $1 < a, b < n$ and $ab = n$ . Regarding a and b as elements of $\integer_n$ , I obtain $ab = 0$ in $\integer_n$ . Therefore, $\integer_n$ has zero divisors, and is not a domain. Since fields are domains, $\integer_n$ is not a field.

Suppose n is prime. The nonzero elements $1, \ldots, n - 1$ are all relatively prime to n. Hence, they are not zero divisors in $\integer_n$ , by the preceding result. Therefore, $\integer_n$ is a domain. Since it's finite, it's a field.

The fields $\integer_p$ for p prime are examples of fields of finite characteristic.

Definition. The characteristic of a ring R is the smallest positive integer n such that $n \cdot r = 0$ for all $r \in R$ . If there is no such integer, the ring has characteristic 0. Denote the characteristic of R by $\char R$ .

$\integer$ , $\real$ , and $\complex$ are fields of characteristic 0. If p is prime, $\integer_p$ is a field of characteristic p.

Proposition. If F is a field of characteristic $n > 0$ , then n is prime.

Proof. If n is composite, write $n = rs$ , where $1 < r, s < n$ . Then

$$(r \cdot 1)(s \cdot 1) = r s \cdot 1 = n \cdot 1 = 0.$$

But $r \cdot 1 \ne 0$ and $s \cdot 1 \ne 0$ since $r, s < n$ . Therefore, F has zero divisors, contradicting the fact that fields are domains.

Note, however, that $\integer_p$ for p prime is not the only field of characteristic p. In fact, for each $n > 0$ , there is a unique field F of characteristic p such that $|F| = p^n$ .

Proposition. Let R be a ring with identity.

(a) If there is no positive integer n such that $n \cdot 1 = 0$ , then $\char R = 0$ .

(b) If $n \cdot 1 = 0$ for some positive integer n, then the smallest positive integer for which this is true is $\char R$ .

Proof. Suppose there is no positive integer n such that $n \cdot 1 = 0$ . If n is a positive integer such that $n \cdot r = 0$ for all $r \in R$ , then in particular $n \cdot 1 = 0$ , which is a contradiction. Therefore, there is no positive integer n such that $n \cdot r = 0$ for all $r \in R$ , and by definition this means that $\char R = 0$ .

Suppose $n \cdot 1 = 0$ for some positive integer n. By Well-Ordering, there is a smallest positive integer m such that $m \cdot 1 = 0$ . If $r \in R$ , then

$$(m \cdot 1) \cdot r = 0 \cdot r, \quad\hbox{or}\quad m \cdot (1 \cdot r) = 0, \quad\hbox{so}\quad m \cdot r = 0.$$

This means that $\char R \ne 0$ , and in fact, $\char R \le m$ . But if $\char R = k < m$ , then $k \cdot 1 = 0$ , which contradicts the assumption that m is the smallest integer such that $m \cdot 1 = 0$ . Therefore, $\char R = m$ .

Definition. An integral domain R is called a principal ideal domain (or PID for short) if every ideal in R is principal.

The integers $\integer$ and polynomial rings over fields are examples of principal ideal domains.

Let's see how this works for a polynomial ring. Consider the set

$$I = \{a(x) \cdot (x^2 - 4) + b(x) \cdot (x^2 - x - 2) \mid a(x), b(x) \in \rational[x]\}.$$

It's straightforward to show that I is an ideal. I'll show that in fact I is principal --- that is, it actually consists of all multiples of a mystery polynomial $f(x)$ .

What could $f(x)$ be? Well, if I take $a(x) = 1$ and $b(x) = 0$ , I see that $x^2 - 4$ is in I. Likewise, $a(x) = 0$ and $b(x) = 1$ shows that $x^2 - x - 2$ is in I. So if everything in I is a multiple of f, then in particular these two polynomials must be multiples of f --- or what is the same, f divides $x^2 - 4$ and $x^2 - x - 2$ .

Note that

$$x^2 - 4 = (x - 2)(x + 2) \quad\hbox{and}\quad x^2 - x - 2 = (x - 2)(x + 1).$$

Now I can see something which divides $x^2 - 4$ and $x^2 - x - 2$ , namely $x - 2$ . I'm going to guess that $f(x) = x - 2$ is my mystery polynomial.

In the first place,

$$a(x) \cdot (x^2 - 4) + b(x) \cdot (x^2 - x - 2) = a(x) \cdot (x - 2)(x + 2) + b(x) \cdot (x - 2)(x + 1).$$

So $x - 2$ divides everything in I.

Now I want to show that anything divisible by $x - 2$ is in I. So suppose $x - 2 \mid g(x)$ , or $g(x) = (x - 2)h(x)$ for some $h(x)$ . Why is $g(x) \in I$ ?

The key is to observe that $x - 2$ is the greatest common divisor of $x^2 - 4$ and $x^2 - x - 2$ . Thus, I can write $x - 2$ as a linear combination of $x^2 - 4$ and $x^2 - x - 2$ . Here's one:

$$x - 2 = (x^2 - 4) - (x^2 - x - 2).$$

Hence,

$$g(x) = \left[(x^2 - 4) - (x^2 - x - 2)\right] h(x) = h(x) \cdot (x^2 - 4) - h(x) \cdot (x^2 - x - 2).$$

The last expression is in I, since it's a linear combination of $x^2 - 4$ and $x^2 - x - 2$ . So $g(x) \in I$ , as I wanted to show.

Therefore, I is principal:

$$I = \langle x - 2\rangle.$$

Now you can see how to do this in a more general case. Suppose you have the ideal

$$\{a_1(x) f_1(x) + \cdots + a_n(x) f_n(x) \mid a_1(x), \ldots, a_n(x) \in F[x]\}.$$

It will be generated by the single element $(f_1(x), \ldots, f_n(x))$ , the greatest common divisor of the f's.

Example. ( Finding a generator for a principal ideal) Consider the ring $\integer[x]$ of polynomials with integer coefficients. Show that the following ideal is not principal:

$$I = \langle x, x + 2 \rangle = \{a(x) (x + 2) + b(x) x \mid a(x), b(x) \in \integer[x]\}.$$

I is an ideal in $\integer[x]$ . It consists of all linear combinations (with polynomial coefficients) of $x + 2$ and x. For example, the following polynomials are elements of I:

$$(x^2 + 5 x + 1)(x + 2) + (x^{117} - 89)(x), \quad (-2 x + 3)(x + 2) + 47 x, \quad (1)(x + 2) + (0)(x), \quad (0)(x + 2) + (1)(x).$$

I'll let you verify that I satisfies the axioms for an ideal. Taking this for granted, I'll show that I is not principal --- that is, I does not consist of multiples of a single polynomial $p(x)$ .

Suppose on the contrary that every element of I is a multiple of a polynomial $p(x) \in \integer[x]$ . Look at the last two sample elements above;

$$x + 2 = (1)(x + 2) + (0)(x) \in I \quad\hbox{and}\quad (0)(x + 2) + (1)(x) = x \in I.$$

Since I is an ideal, their difference $(x + 2) - x = 2$ is also an element of I.

By assumption, every element of I is a multiple of $p(x)$ , so 2 is a multiple of $p(x)$ . Thus, $2 = a(x)p(x)$ for some polynomial $a(x)$ .

However, the only integer polynomials which divide the polynomial 2 are $\pm 1$ and $\pm 2$ . So $p(x)$ is -1, 1, -2, or 2.

x is also an element of I, so x is a multiple of $p(x)$ . Of the possibilities -1, 1, -2, or 2, only -1 and 1 divide x. So $p(x) = 1$ or $p(x) = -1$ .

However, remember that elements of I have the form $a(x) (x + 2) + b(x) (x)$ . The constant term of this polynomial is the constant term of $a(x)$ times 2 --- that is, the constant term must be divisible by 2. Since neither 1 nor -1 are divisible by 2, it follows that $p(x)$ can't be 1 or -1.

This contradiction shows that there is no such $p(x)$ : The ideal I is not principal.

Consequently, $\integer[x]$ is not a principal ideal domain.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga