Modular Arithmetic

Modular arithmetic is a way of systematically ignoring differences involving a multiple of an integer. If n is an integer, two integers are equal mod n if they differ by a multiple of n; it is as if multiples of n are "set equal to 0".

Definition. Let n, x, and y be integers. x is congruent to y mod n if $n \mid x - y$ . Notation:

$$x = y \mod{n}.$$

Remarks. $n \mid x - y$ is equivalent to the following statements:

(a) $n \mid y - x$ .

(b) $x = y + j n$ for some $j \in \integer$ .

(c) $y = x + k n$ for some $k \in \integer$ .

I'll often use any of these four statements as the definition of $x = y \mod{n}$ .

A lot of people like to write "$x \cong y \mod{n}$ " instead of "$x = y \mod{n}$ ". I don't think there's any harm in using an ordinary equal sign, since the "$\mod{n}$ " makes the meaning clear. It's also a bit shorter to write.

Example. ( Examples of congruences with numbers) (a) Demonstrate that $7 = 1 \mod{6}$ and $57 = -13 \mod{7}$ .

(b) Express "x is even" and "x is odd" in terms of congruences.

(c) What does $x = 0 \mod{n}$ means in terms of divisibility?

(a)

$$7 = 1 \mod{6}, \quad\hbox{since}\quad 6 \mid 7 - 1.$$

$$57 = -13 \mod{7}, \quad\hbox{since}\quad 7 \mid 57 - (-13).$$

(b) x is even if and only if $x = 0 \mod{2}$ and x is odd if and only if $x = 1 \mod{2}$ .

(c) $x = 0 \mod{n}$ if and only if $n \mid x$ . Thus, congruences provide a convenient notation for dealing with divisibility relations.

The following proposition says that you can work with modular equations in many of the ways that you work with ordinary equations.

Proposition. Let $n \in \integer$ .

(a) If $a = b \mod{n}$ and $c = d \mod{n}$ , then

$$a + c = b + d \mod{n}.$$

(b) If $a = b \mod{n}$ and $c = d \mod{n}$ , then

$$a c = b d \mod{n}.$$

(c) If $a = b \mod{n}$ , then

$$a c = b c \mod{n}.$$

Proof. Two ideas for these kinds of proofs:

1. You can often prove statements about congruences by reducing them to statements about divisibility.

2. You can often prove statements about divisibility by reducing them to (ordinary) equations.

(a) Suppose $a = b \mod{n}$ and $c = d \mod{n}$ .

$a = b \mod{n}$ means $n \mid a - b$ and $c = d \mod{n}$ means $n \mid c - d$ . By properties of divisibility,

$$n \mid (a - b) + (c - d) = (a + c) - (b + d).$$

Therefore, $a + c = b + d \mod{n}$ .

(b) Suppose $a = b \mod{n}$ and $c = d \mod{n}$ .

$a = b \mod{n}$ means $n \mid a - b$ , which means $a - b = j n$ for some $j \in \integer$ . $c = d \mod{n}$ means $n \mid c - d$ , which means $c - d = k n$ for some $k \in \integer$ . Thus, $a = b + j n$ , $c = d + k n$ , and hence

$$a c = (b + j n)(d + k n) = b d + b k n + d j n + j k n^2 = b d + n(b k + d j + j k n).$$

This gives $a c - b d = n(b k + d j + j k n)$ , so $n \mid a c - b d$ , and hence $a c = b d \mod{n}$ .

(c) Suppose $a = b \mod{n}$ . This means that $n \mid a - b$ . By properties of divisibility,

$$n \mid (a - b)c = a c - b c.$$

Therefore, $a c = b c \mod{n}$ .

Example. ( Solving a congruence) Solve $3 x + 4 = 2 x + 8 \mod{9}$ .

In this case, I'll solve the modular equation by adding or subtracting the same thing from both sides.

$$\matrix{& 3 x & + & 4 & = & 2 x & + & 8 & \mod{9} \cr - & & & 4 & = & & & 4 & \mod{9} \cr \noalign{\vskip2 pt\hrule\vskip2 pt} & 3 x & & & = & 2 x & + & 4 & \mod{9} \cr - & 2 x & & & = & 2 x & & & \mod{9} \cr \noalign{\vskip2 pt\hrule\vskip2 pt} & x & & & = & & & 4 & \mod{9} \cr}$$

The solution is $x = 4 \mod{9}$ .

Example. Reduce $497 \cdot 498 \cdot 499 \mod{500}$ to a number in the range $\{0, 1, \ldots 499\}$ , doing the computation by hand.

Note that

$$497 = -3 \mod{500}, \quad 498 = -2 \mod{500}, \quad 499 = -1 \mod{500}.$$

So

$$497 \cdot 498 \cdot 499 = (-3)(-2)(-1) = -6 = 494 \mod{500}.\quad\halmos$$

The next result says that congruence mod n is an equivalence relation.

Proposition.

(a) (Reflexivity) $a = a \mod n$ for all $a \in \integer$ .

(b) (Symmetry) Let $a, b \in \integer$ . If $a = b \mod n$ , then $b = a \mod n$ .

(c) (Transitivity) Let $a, b, c \in \integer$ . If $a = b \mod n$ and $b = c \mod n$ , then $a = c \mod n$ .

Proof. (a) If $a \in \integer$ , then $n \mid a - a$ , so $a = a \mod{n}$ .

(b) If $a = b \mod n$ , then $n \mid a - b$ , so $n \mid -(a - b) = b - a$ . Therefore, $b = a \mod n$ .

(c) Suppose $a = b \mod n$ and $b = c \mod n$ . $a = b \mod{n}$ means $n \mid a - b$ ; $b = c \mod{n}$ means $n \mid b - c$ . Therefore,

$$n \mid (a - b) + (b - c) = a - c.$$

Hence, $a = c \mod n$ .

An equivalence relation on a set gives rise to a partition of the set into equivalence classes. In the case of congruence mod n, an equivalence class consists of integers congruent to each other mod n.

Definition. $\integer_n$ (read "Z mod n") is the set of equivalence classes under congruence mod n.

Example. ( Congruence classes mod 3) Find the equivalence classes of the relation congruence mod 3 on the set of integers.

Relative to the equivalence relation of congruence mod 3 on $\integer$ , the integers break up into three disjoint sets:

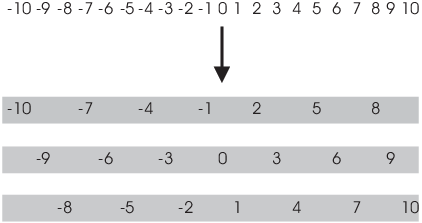
$$\hbox{\epsfysize=2 in \epsffile{modular-arithmetic1.eps}}$$

All the elements of a given set are congruent mod 3, and no element in one set is congruent mod 3 to an element of another. The sets divide up the integers like three puzzle pieces.

It's cumbersome to write and use equivalence classes as is, since each equivalence class is a set (infinite, in this case). It's customary to choose a representative from each equivalence class and use the representatives to do arithmetic. I'll choose

$$0 \quad\hbox{from}\quad \{\ldots, -9, -6, -3, 0, 3, 6, 9, \ldots\},$$

$$1 \quad\hbox{from}\quad \{\ldots, -8, -5, -2, 1, 4, 7, 10, \ldots\},$$

$$2 \quad\hbox{from}\quad \{\ldots, -7, -4, -1, 2, 5, 8, 11, \ldots\}.$$

I'll abuse notation and write

$$\integer_3 = \{0, 1, 2\}.$$

$\integer_3$ is called the cyclic group of order 3. The "cyclic" nature of $\integer_3$ can be visualized by arranging the integers in a spiral, with each congruence class on a ray.

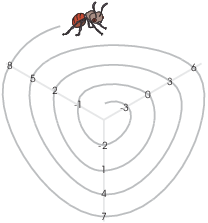
$$\hbox{\epsfysize=2 in \epsffile{modular-arithmetic2.eps}}$$

When you do arithmetic in $\integer_3$ , it is as if you count in a circle: 0, 1, 2, then back to 0 again.

You can form other cyclic groups in an analogous way. For example,

$$\integer_6 = \{0, 1, 2, 3, 4, 5\}.\quad\halmos$$

You can do arithmetic in $\integer_n$ by adding and multiplying as usual, but reducing the results mod n.

Example. ( Operation tables for $\integer_3$ ) Construct addition and multiplication tables for $\integer_3$ .

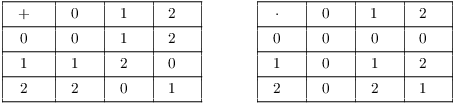
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.5 in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

For example, as integers $2 + 2 = 4$ . I divide 4 by the modulus 3 and get a remainder of 1. Hence, $2 + 2 = 1$ .

Likewise, $2 \cdot 2 = 4 = 1$ in $\integer_3$ .

Example. ( Equations in $\integer_n$ ) Find $6 \cdot 7$ in $\integer_{11}$ , $13 + 19$ in $\integer{21}$ , and -8 in $\integer_{17}$ .

$$6 \cdot 7 = 9 \quad\hbox{in}\quad \integer_{11}.$$

$$13 + 19 = 11 \quad\hbox{in}\quad \integer_{21}.$$

$$-8 = 9 \quad\hbox{in}\quad \integer_{17}.$$

-8 means the additive inverse of 8. The last statement is just another way of saying $-8 = 9 \mod{17}$ .

Example. ( Using modular arithmetic in a divisibility proof) Prove that if n is an integer, then $2 n^2 + 3 n + 2$ is not divisible by 5.

Every integer n is congruent to one of 0, 1, 2, 3, or 4 mod 5. Therefore, I have 5 cases. In each case, I want to show that $2 n^2 + 3 n + 2$ is not divisible by 5 --- or to say it in terms of congruences, I want to show that $2 n^2 + 3 n + 2 \ne 0 \mod{5}$ .

I set $n = 0, 1, 2, 3, 4 \mod{5}$ and "substitute" the value into $2 n^2 + 3 n + 2$ . This substitution is justified by the properties of congruences I discussed above.

For example, if $n = 3 \mod{5}$ , then

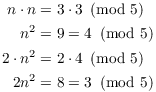
$$\eqalign{ n \cdot n & = 3 \cdot 3 \mod{5} \cr n^2 & = 9 = 4 \mod{5} \cr 2 \cdot n^2 & = 2 \cdot 4 \mod{5} \cr 2 n^2 & = 8 = 3 \mod{5} \cr}$$

Likewise, $3 n = 3\cdot 3 = 9 = 4 \mod{5}$ . So

$$2 n^2 + 3 n + 2 = 3 + 4 + 2 = 9 = 4 \mod{5}.$$

Essentially, I can plug $n = 3$ into $2 n^2 + 3 n + 2$ , then reduce the result mod 5 to one of 0, 1, 2, 3, or 4.

Continuing in this way, I get the following table:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $n \mod{5}$ & & 0 & & 1 & & 2 & & 3 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $2 n^2 + 3 n + 2 \mod{5}$ & & 2 & & 2 & & 1 & & 4 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

In all five cases, $2 n^2 + 3 n + 2 \ne 0 \mod{5}$ . Therefore, $2 n^2 + 3 n + 2$ is never divisible by 5.

I showed earlier how to use algebraic operations to solve simple modular equations. How would you solve something like this:

$$6 x = 13 \mod{25}?$$

I'd like to divide both sides by 6, but I only know how to add and multiply. I can subtract, but that's because I can add additive inverses. Well, division is multiplication by the multiplicative inverse; what is a multiplicative inverse mod 25?

Definition. Let $a, b \in \integer_n$ . a and b are multiplicative inverses if $ab = 1 \mod{n}$ (or $ab = 1$ in $\integer_n$ ).

If a is the multiplicative inverse of b, you can write $a = b^{-1}$ .

(You don't write "$\dfrac{1}{b}$ " unless you're in a number system like the rational numbers where fractions are in use.)

Example. ( Modular multiplicative inverses) (a) Prove that 6 and 2 are multiplicative inverses mod 11.

(b) Show that 8 does not have a multiplicative inverse mod 12.

(a) $6 \cdot 2 = 1 \mod{11}$ .

(b) One tedious way is to take cases:

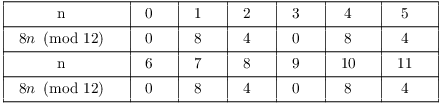
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & n & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $8 n \mod{12}$ & & 0 & & 8 & & 4 & & 0 & & 8 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & n & & 6 & & 7 & & 8 & & 9 & & 10 & & 11 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $8 n \mod{12}$ & & 0 & & 8 & & 4 & & 0 & & 8 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

No number multiplied by 8 gives 1 mod 12.

I could try all the possibilities because the numbers were small. How would you do this kind of problem if the numbers were larger?

One approach is to simply appeal to the result following this example. However, I can also give a proof by contradiction.

Suppose that 8 has a multiplicative inverse mod 12. Let x be the multiplicative inverse. Then $8 x = 1 \mod{12}$ . Multiplying both sides by 3, I get

$$24 x = 3 \mod{12}, \quad\hbox{or}\quad 0 = 3 \mod{12}.$$

This is a contradiction, since 0 and 3 do not differ by a multiple of 12. Therefore, 8 does not have a multiplicative inverse mod 12.

Proposition. $m \in \integer_n$ has a multiplicative inverse if and only if $(m, n) = 1$ .

Proof. Suppose $m \in \integer_n$ has a multiplicative inverse, so

$$k m = 1 \quad\hbox{for some}\quad k \in \integer_n.$$

I can regard this as a statement in $\integer$ :

$$k m = 1 \mod{n}.$$

This means that $km$ and 1 differ by a multiple of n:

$$k m - 1 = a n \quad\hbox{for some}\quad a \in \integer.$$

Thus,

$$k m - a n = 1.$$

This is a linear combination of m and n which gives 1. Therefore, $(m, n) = 1$ .

Conversely, suppose $(m, n) = 1$ . I may find integers a and b such that

$$a m + b n = 1.$$

That is,

$$a m = 1 \mod{n}.$$

Now regarded as an equation in $\integer_n$ , this says

$$a m = 1 \quad\hbox{in}\quad \integer_n.$$

That is, m has multiplicative inverse a.

Example. ( Using the Extended Euclidean algorithm to find modular inverses) Find the multiplicative inverse of 31 in $\integer_{52}$ .

Note that $(31, 52) = 1$ . Apply the Extended Euclidean Algorithm:

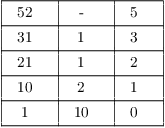
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 52 & & - & & 5 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 31 & & 1 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 21 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 10 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 10 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus,

$$1 = 3\cdot 52 + (-5 )\cdot 31.$$

In $\integer_{52}$ , $52 = 0$ and $-5 = 47$ . The equation says $1 = 47 \cdot 31$ . Thus, 47 is the multiplicative inverse of 31 in $\integer_{52}$ .

Theorem. If $(a, n) = 1$ , then the following equation has a unique solution:

$$a x = b \quad\hbox{in}\quad \integer_n.$$

Proof. If $(a, n) = 1$ , then a has a multiplicative inverse $a^{-1}$ in $\integer_n$ . Thus, $a a^{-1} = 1$ in $\integer_n$ .

First, this means that $x = a^{-1}b$ is a solution, since

$$a(a^{-1} b) = (a a^{-1}) b = 1 \cdot b = b.$$

Second, if $x'$ is another solution, then $a x' = b$ . Multiplying both sides by $a^{-1}$ , I get

$$a^{-1} a x' = a^{-1} b, \quad x' = a^{-1} b.$$

That is, $x' = x$ . This means the solution is unique.

Example. ( Solving modular equations using modular inverses) Solve

$$13 x = 12 \mod{15}.$$

There is a solution, since $(13, 15) = 1$ . I need to find a multiplicative inverse for 13 mod 15.

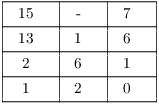
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 15 & & - & & 7 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 13 & & 1 & & 6 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & 6 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The Extended Euclidean Algorithm says that

$$(-6)(15) + (7)(13) = 1.$$

Hence, $7\cdot 13 = 1 \mod{15}$ , i.e. 7 is the multiplicative inverse of 13 mod 15.

Multiply the original equation by 7:

$$7\cdot 13 x = 7\cdot 12 \mod{15}, \quad x = 84 = 9 \mod{15}.\quad\halmos$$

Proposition. Suppose

$$a c = b c \mod{n}.$$

Then

$$a = b \mod{\dfrac{n}{(n, c)}}.$$

Proof. I have

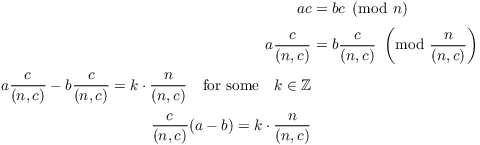
$$\eqalign{ a c & = b c \mod{n} \cr \noalign{\vskip2pt} a \dfrac{c}{(n, c)} & = b \dfrac{c}{(n, c)} \mod{\dfrac{n}{(n, c)}} \cr \noalign{\vskip2pt} a \dfrac{c}{(n, c)} - b \dfrac{c}{(n, c)} = k \cdot \dfrac{n}{(n, c)} \quad\hbox{for some}\quad k \in \integer \cr \noalign{\vskip2pt} \dfrac{c}{(n, c)} (a - b) = k \cdot \dfrac{n}{(n, c)} \cr}$$

(Note that $(n, c) \mid c$ and $(n, c) \mid n$ , so $\dfrac{c}{(n, c)}$ and $\dfrac{n}{(n, c)}$ are actually integers.) Now $\dfrac{n}{(n, c)}$ divides $\dfrac{c}{(n, c)} (a - b)$ , but

$$\left(\dfrac{n}{(n, c)}, \dfrac{c}{(n, c)}\right) = 1.$$

By Euclid's lemma, $\dfrac{n}{(n, c)} \mid a - b$ . Hence,

$$a = b \mod{\dfrac{n}{(n, c)}}.\quad\halmos$$

I can use the preceding result to solve some congruences when I can't immediately use modular inversion.

Example. Solve

$$12 x = 30 \mod{34}.$$

Since $(12, 34) = 2 \ne 1$ , 12 doesn't have a multiplicative inverse mod 34. I'll use the preceding result. I "cancel" a factor of 6 from $12 x$ and 30, and divide the modulus 34 by $(6, 34) = 2$ :

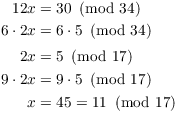
$$\eqalign{ 12 x & = 30 \mod{34} \cr 6 \cdot 2 x & = 6 \cdot 5 \mod{34} \cr \noalign{\vskip2pt} 2 x & = 5 \mod{17} \cr 9 \cdot 2 x & = 9 \cdot 5 \mod{17} \cr x & = 45 = 11 \mod{17} \cr}$$

Since the original congruence was mod 34, I must find all numbers in $\{0, 1, 2, \ldots 33\}$ which satisfy $x = 11 \mod{17}$ . One is obviously 11. Adding 17, I find that $11 + 17 = 28$ also works. (Adding 17 again takes me out of the set $\{0, 1, 2, \ldots 33\}$ .)

The solutions are $x = 11 \mod{17}$ and $x = 28 \mod{17}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga