Normal Subgroups and Quotient Groups

Under what conditions will the set of cosets form a group? That is, under what conditions will coset addition or multiplication be well-defined?

If H is a subgroup of a group G, I'd like to multiply two cosets of H this way:

$$a H \cdot b H = (a b) H.$$

Here's the problem. A coset like $a H$ can be represented by different elements: That is, I can have $a H = a' H$ where $a \ne a'$ . Remember that a coset $a H$ is a set of elements, not a single element. For example, if you consider cosets of the subgroup $2 \integer$ in $\integer$ ,

$$1 + 2 \integer = 13 + 2 \integer.$$

Both of these sets consist of all the odd integers, even though $1 \ne 13$ .

So in writing $a H \cdot b H = (a b) H$ , I should be able to replace $a H$ with $a' H$ , since they're equal. Then I'd get

$$a' H \cdot b H = (a' b) H.$$

I should have $(a b) H = (a' b) H$ , because the two cosets I multiplied were the same in both cases. But how do I know this will work? For that matter, what if I replace $b H$ with $b' H$ , using a different representative for the second coset?

It turns out that this doesn't work in general: I need to have a condition on the subgroup H.

Definition. A subgroup $H < G$ is normal if

$$g H g^{-1} \subset H \quad\hbox{for all}\quad g \in G.$$

The notation $H \triangleleft G$ means that H is a normal subgroup of G.

Remark. (a) Since the statement runs over all $g \in G$ , I can replace "g" in the definition with "$g^{-1}$ ", because every $g \in G$ is the inverse of some element, namely $g^{-1}$ ). Thus, I could just as well say "$g^{-1} H g \subset H$ ".

(b) As usual, to check the set inclusion $g H g^{-1} \subset H$ , you can verify that it holds for elements: Let $h \in H$ and $g \in G$ , and show that $g h g^{-1} \in H$ .

(c) For a fixed $g \in G$ , I have $g H g^{-1} \subset H$ . But I also have

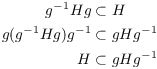
$$\eqalign{ g^{-1} H g & \subset H \cr g (g^{-1} H g) g^{-1} & \subset g H g^{-1} \cr H & \subset g H g^{-1} \cr}$$

Hence, $g H g^{-1} = H$ . So I actually have equality, not just subset inclusion. If you're showing a subgroup is normal, you are better off doing less work and just proving inclusion, as in the definition: You get equality for free.

The next two results give some easy examples of normal subgroups.

Proposition. Let G be a group. Then $\{1\}$ and G are normal subgroups of G.

Proof. To show that $\{1\}$ is normal, let $g \in G$ . The only element of $\{1\}$ is 1, and $g \cdot 1 \cdot g^{-1} = 1 \in \{1\}$ . Therefore, $\{1\}$ is normal.

To show that G is normal, let $g \in G$ and let $h \in G$ . Then $g h g^{-1} \in G$ , because g, h, and $g^{-1}$ are all in G, and G must be closed under its operation.

Proposition. If G is abelian, every subgroup is normal.

Proof. If $g \in G$ , then $g H g^{-1} = H g g^{-1} = H$ .

Example. ( Showing a subgroup is not normal) Show that the subgroup $\{\hbox{id}, (1\ 3)\}$ of $S_3$ is not normal.

Here's the multiplication table for $S_3$ , the group of permutations of $\{1, 2, 3\}$ .

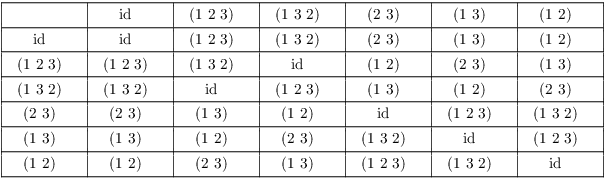
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\id$ & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 2\ 3) & & (1\ 2\ 3) & & (1\ 3\ 2) & & $\id$ & & (1\ 2) & & (2\ 3) & & (1\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 3\ 2) & & (1\ 3\ 2) & & $\id$ & & (1\ 2\ 3) & & (1\ 3) & & (1\ 2) & & (2\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (2\ 3) & & (2\ 3) & & (1\ 3) & & (1\ 2) & & $\id$ & & (1\ 2\ 3) & & (1\ 3\ 2) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 3) & & (1\ 3) & & (1\ 2) & & (2\ 3) & & (1\ 3\ 2) & & $\id$ & & (1\ 2\ 3) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1\ 2) & & (1\ 2) & & (2\ 3) & & (1\ 3) & & (1\ 2\ 3) & & (1\ 3\ 2) & & $\id$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I have to find an element $g \in S_3$ such that

$$g \{\hbox{id}, (1\ 3)\} g^{-1} \not\subset \{\hbox{id}, (1\ 3)\}.$$

There are several possibilities. For example,

$$(1\ 2) \{\hbox{id}, (1\ 3)\} (1\ 2)^{-1} = (1\ 2) \{\hbox{id}, (1\ 3)\} (1\ 2) = \{(1\ 2) \hbox{id} (1\ 2), (1\ 2) (1\ 3) (1\ 2)\} = \{\hbox{id}, (2\ 3)\}.$$

Since $\{\hbox{id}, (2\ 3)\} \not\subset \{\hbox{id}, (1\ 3)\}$ , the subgroup $\{\hbox{id}, (1\ 3)\}$ is not normal in $S_3$ .

Example. ( A normal subgroup of the quaternions) Show that the subgroup $\{1, -1, i, -i\}$ of the group of quaternions is normal.

Here's the multiplication table for the group of the quaternions:

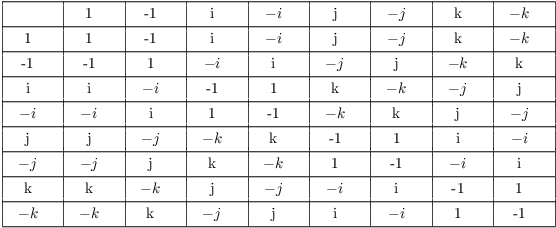
$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & -1 & & i & & $-i$ & & j & & $-j$ & & k & & $-k$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & -1 & & -1 & & 1 & & $-i$ & & i & & $-j$ & & j & & $-k$ & & k & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & i & & i & & $-i$ & & -1 & & 1 & & k & & $-k$ & & $-j$ & & j & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-i$ & & $-i$ & & i & & 1 & & -1 & & $-k$ & & k & & j & & $-j$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & j & & j & & $-j$ & & $-k$ & & k & & -1 & & 1 & & i & & $-i$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-j$ & & $-j$ & & j & & k & & $-k$ & & 1 & & -1 & & $-i$ & & i & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & k & & k & & $-k$ & & j & & $-j$ & & $-i$ & & i & & -1 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $-k$ & & $-k$ & & k & & $-j$ & & j & & i & & $-i$ & & 1 & & -1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

To show that the subgroup is normal, I have to compute $g\{1, -1, i, -i\}g^{-1}$ for each element g in the group and show that I always get the subgroup $\{1, -1, i, -i\}$ .

It's a bit tedious to do this for all the elements, so I'll just do the computation for one of them by way of example.

Take $g = j$ . Then $g^{-1} = -j$ (since $j(-j) = 1$ ), so

$$j\{1, -1, i, -i\}j^{-1} = j\{1, -1, i, -i\}(-j) = \{j \cdot 1 \cdot (-j), j \cdot (-1) \cdot (-j), j \cdot i \cdot (-j), j \cdot (-i) \cdot (-j)\} =$$

$$\{1, -1, (-k)(-j), k(-j)\} = \{1, -1, -i, i\}.$$

This is the same set as the original subgroup, so the verification worked with this element.

If I do the same computation with the other elements in Q, I'll always get the original subgroup back. Therefore, $\{1, -1, i, -i\}$ is normal.

As this example indicates, it is generally infeasible to show a subgroup is normal by checking the definition for all the elements in the group!

Here's another special case where subgroups satisfying a certain condition are normal.

Proposition. Let H be a subgroup of G. If $(G : H) = 2$ , then H is normal.

Proof. Since $(G : H) = 2$ , I know that H has two left cosets and two right cosets. One coset is always H itself. Take $g \notin H$ . Then $g H$ is the other left coset, $H g$ is the other right coset, and

$$H \cup g H = G = H \cup H g.$$

But these are disjoint unions, so $g H = H g$ , and therefore $g H g^{-1} = H$ . This equation holds for any g in the coset $g H$ . The equation clearly holds for any element of the trivial coset H. Hence, the equation holds for all elements of G, and H is normal.

Example. Show that the alternating group $A_n$ is a normal subgroup of $S_n$ .

The even permutations make up half of $S_n$ , so $(S_n : A_n) = 2$ . Therefore, $A_n$ is normal.

Example. ( Checking normality in a product) Let G and H be groups. Let

$$G \times \{1\} = \{(g, 1) \mid g \in G\}.$$

Prove that $G \times \{1\}$ is a normal subgroup of the product $G \times H$ .

First, I'll show that it's a subgroup.

Let $(g_1, 1), (g_2, 1) \in G \times \{1\}$ , where $g_1, g_2 \in G$ . Then

$$(g_1, 1)\cdot (g_2, 1) = (g_1 g_2, 1) \in G \times \{1\}.$$

Therefore, $G \times \{1\}$ is closed under products.

The identity $(1, 1)$ is in $G \times \{1\}$ .

If $(g, 1) \in G \times \{1\}$ , the inverse is $(g, 1)^{-1} = (g^{-1}, 1)$ , which is in $G \times \{1\}$ .

Therefore, $G \times \{1\}$ is a subgroup.

To show that $G \times \{1\}$ is normal, let $(a, b) \in G \times H$ , where $a \in G$ and $b \in H$ . I must show that

$$(a, b)(G \times \{1\})(a, b)^{-1} \subset G \times \{1\}.$$

I can show one set is a subset of another by showing that an element of the first is an element of the second. An element of $(a, b)(G \times \{1\})(a, b)^{-1}$ looks like $(a, b)(g, 1)(a, b)^{-1}$ , where $(g, 1) \in G \times \{1\}$ . Now

$$(a, b)(g, 1)(a, b)^{-1} = (a, b)(g, 1)(a^{-1}, b^{-1}) = (a g a^{-1}, b(1)b^{-1}) = (a g a^{-1}, 1).$$

$a g a^{-1} \in G$ , since $a, g \in G$ . Therefore, $(a, b)(g, 1)(a, b)^{-1} \in G \times \{1\}$ . This proves that $(a, b)(G \times \{1\})(a, b)^{-1} \subset G \times \{1\}$ . Therefore, $G \times \{1\}$ is normal.

Now I need to show that the condition of normality allows me to turn the set of cosets of a subgroup into a quotient group under coset multiplication or addition. I need a few preliminary results on cosets first.

Theorem. Let G be a group, and let H be a subgroup of G. The following statements are equivalent:

(a) a and b are elements of the same coset of H.

(b) a H = b H.

(c) $b^{-1} a \in H$ .

Proof. To show that several statements are equivalent, I must show that any one of them follows from any other. To do this efficiently, I'll show that statement (a) implies statement (b), statement (b) implies statement (c), and statement (c) implies statement (a).

((a) $\ifthen$ (b)) Suppose a and b are elements of the same coset $g H$ of H. Since $a \in a H \cap g H$ , and since cosets are either disjoint or identical, $aH = gH$ . Likewise, $b \in b H \cap g H$ implies $b H = g H$ . Therefore, $a H = b H$ .

((b) $\ifthen$ (c)) Suppose $a H = b H$ . Since $1 \in H$ , it follows that $a = a \cdot 1 \in a H = b H$ . Therefore, $a = b h$ for some $h \in H$ . Hence, $b^{-1} a = h \in H$ .

((c) $\ifthen$ (a)) Suppose $b^{-1} a = h \in H$ . Then $b^{-1} a H = h H = H$ , so $a H = b H$ . Therefore, a and b are elements of the same coset of H, namely $a H = b H$ .

Corollary. $a H = H$ if and only if $a \in H$ .

Proof. The equivalence of the second and third conditions says that $a H = b H$ if and only if $b^{-1} a \in H$ . Taking $b = 1$ , this says that $a H = H$ if and only if $a \in H$ , which is what I wanted to prove.

Now I'll show that the definition of normality does what I wanted it to.

Theorem. Let G be a group, $H < G$ . The following statements are equivalent:

(a) $H \triangleleft G$

(b) For all $g \in G$ , $g H = H g$ . (Thus, every left coset is a right coset and every right coset is a left coset.)

(c) Coset multiplication is well-defined.

By (c), I mean that if $a_1 H = a_2 H$ and $b_1 H = b_2 H$ , then $a_1 b_1 H = a_2 b_2 H$ . Once I know that multiplication is well-defined, I can define multiplication of cosets by $(a H)(b H) = (a b) H$ .

Proof. ((a) $\ifthen$ (b)) If $H \triangleleft G$ and $g \in G$ , then $g H g^{-1} = H$ , so $g H g^{-1} g = H g$ , or $g H = H g$ .

((b) $\ifthen$ (c)) Suppose $g H = H g$ for all $g \in G$ . Suppose

$$a_1 H = a_2 H \quad\hbox{and}\quad b_1 H = b_2 H.$$

Then

$$a_1 b_1 H = a_1 b_2 H = a_1 H b_2 = a_2 H b_2 = a_2 b_2 H.$$

((c) $\ifthen$ (a)) Suppose coset multiplication is well defined. I want to show $H \triangleleft G$ . Let $g \in G$ . I will show $g H g^{-1} \subset H$ .

Let $h \in H$ . I will show $g h g^{-1} \in H$ .

By an earlier result, $h H = 1 H$ , and surely $g H = g H$ , so (since coset multiplication is well-defined)

$$\eqalign{ (g H)(h H) & = (g H)(1 H) \cr (g h) H & = g H \cr}$$

And since $g^{-1} H = g^{-1} H$ ,

$$\eqalign{ [(g h) H] (g^{-1} H) & = (g H)(g^{-1} H) \cr (g h g^{-1}) H & = (g g^{-1}) H \cr (g h g^{-1}) H & = H \cr}$$

An earlier result shows that this implies $g h g^{-1} \in H$ . Therefore, $H \triangleleft G$ .

The point of all this was to make the set of cosets $G/H$ into a group via coset multiplication or addition.

Theorem. If $H \triangleleft G$ , the set of left cosets $G/H$ becomes a group under coset multiplication.

Proof. I'll check that axioms. For associativity, note that

$$(a H \cdot b H) \cdot c H = (a b) H \cdot c H = (a b c) H \quad\hbox{and}\quad a H \cdot (b H \cdot c H) = a H \cdot (b c) H = (a b c) H.$$

I have

$$1 H \cdot a H = a H = a H \cdot 1 H \quad\hbox{for all}\quad a \in G.$$

Hence, $H = 1 H$ is the identity for coset multiplication.

Finally

$$a H \cdot a^{-1} H = 1 H = a^{-1} H \cdot a H \quad\hbox{for all}\quad a \in G.$$

Therefore, $(a H)^{-1} = a^{-1} H$ , and every coset has an inverse.

Definition. Let G be a group, and let $H \normal G$ . The set $G/H$ of left cosets under coset multiplication is the quotient group (or factor group) of G by H.

Because coset multiplication (or addition) is independent of the choice of representatives, you do computations in quotient groups by doing the corresponding computations on coset representatives. The following examples illustrate this idea.

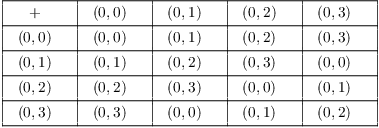
Example. ( Adding cosets) Let $G = \integer_8 = \{0, 1, 2, 3, 4, 5, 6, 7\}$ and let H be the subgroup $\{0, 4\}$ .

(a) List the cosets of $\{0, 4\}$ .

(b) Construct the addition table for the quotient group $\dfrac{\integer_8}{\{0, 4\}}$ using coset addition as the operation.

(c) Identify the quotient group as a familiar group.

(a) The cosets of H are

$$\{0, 4\}, \quad 1 + \{0, 4\} = \{1, 5\}, \quad 2 + \{0, 4\} = \{2, 6\}, \quad 3 + \{0, 4\} = \{3, 7\}.$$

(b) Make the set of cosets $\dfrac{\integer_8}{\{0, 4\}}$ into a group by using coset addition. This means that to add two cosets you add their representatives, then take the coset containing the sum as the sum of the cosets. Here's the addition table:

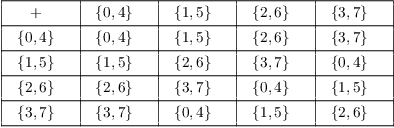
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & $\{0, 4\}$ & & $\{1, 5\}$ & & $\{2, 6\}$ & & $\{3, 7\}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\{0, 4\}$ & & $\{0, 4\}$ & & $\{1, 5\}$ & & $\{2, 6\}$ & & $\{3, 7\}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\{1, 5\}$ & & $\{1, 5\}$ & & $\{2, 6\}$ & & $\{3, 7\}$ & & $\{0, 4\}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\{2, 6\}$ & & $\{2, 6\}$ & & $\{3, 7\}$ & & $\{0, 4\}$ & & $\{1, 5\}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\{3, 7\}$ & & $\{3, 7\}$ & & $\{0, 4\}$ & & $\{1, 5\}$ & & $\{2, 6\}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

To see how the table was constructed, consider the entry

$$\{2, 6\} + \{3, 7\} = \{1, 5\}.$$

Use representatives for the cosets:

$$\{2, 6\} = 2 + \{0, 4\} \quad\hbox{and}\quad \{3, 7\} = 3 + \{0, 4\}.$$

You add cosets by adding their representatives --- in this case, 2 and 3 --- and attaching the sum to the subgroup --- in this case, $\{0, 4\}$ :

$$\{2, 6\} + \{3, 7\} = (2 + \{0, 4\}) + (3 + \{0, 4\}) = (2 + 3) + \{0, 4\} = 5 + \{0, 4\} = \{1, 5\}.$$

You can also use individual elements. Take an element from $\{2, 6\}$ and an element from $\{3, 7\}$ and add them. Find the coset that contains the sum. That coset is the sum of the cosets.

For example, if I use 6 from $\{2, 6\}$ and 3 from $\{3, 7\}$ , I get $6 + 3 = 1$ , which is in $\{1, 5\}$ . Therefore, $\{2, 6\} + \{3, 7\} = \{1, 5\}$ .

What happens if you choose different elements? Take 2 from $\{2, 6\}$ and 7 from $\{3, 7\}$ . Then $2 + 7 = 1$ , which is in $\{1, 5\}$ again. Just as before, $\{2, 6\} + \{3, 7\} = \{1, 5\}$ .

This is what it means to say that coset addition is well-defined: No matter which elements you choose from the two sets, the sum of the elements will always be in the same coset.

(c) The table above is a group table for a group of order 4. There are only two groups of order 4: $\integer_4$ and $\integer_2 \times \integer_2$ . Hence, the group above must be isomorphic to one of these groups. Replace

$$\{0, 4\} \quad\hbox{with}\quad 0, \quad \{1, 5\} \quad\hbox{with}\quad 1, \quad \{2, 6\} \quad\hbox{with}\quad 2, \quad\hbox{and}\quad \{3, 7\} \quad\hbox{with}\quad 3.$$

This gives the table:

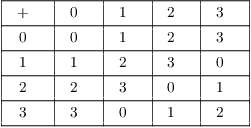
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 3 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 3 & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Thus, $\dfrac{\integer_8}{\{0, 4\}} \approx \integer_4$ .

Example. The cosets of the subgroup $\langle 19 \rangle$ in $U_{20}$ are

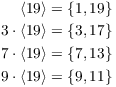
$$\eqalign{ \langle 19 \rangle & = \{1, 19\} \cr 3 \cdot \langle 19 \rangle & = \{3, 17\} \cr 7 \cdot \langle 19 \rangle & = \{7, 13\} \cr 9 \cdot \langle 19 \rangle & = \{9, 11\} \cr}$$

(a) Compute $\{3, 17\} \cdot \{9, 11\}$ .

(b) Compute $\{3, 17\}^{-1}$ .

(c) Compute $\{9, 11\}^3$ .

(d) Construct a multiplication table for the quotient group $\dfrac{U_{20}}{\langle 19 \rangle}$ . Determine whether the quotient group is isomorphic to $\integer_4$ or to $\integer_2 \times \integer_2$ .

(a) Take an element (it doesn't matter which one) from each coset, say $3 \in \{3, 17\}$ and $11 \in \{9, 11\}$ .

Perform the operation on the elements you chose. In this case, it's multiplication:

$$3 \cdot 11 = 33 = 13.$$

Find the coset containing the answer: $13 \in \{7, 13\}$ .

Hence,

$$\{3, 17\} \cdot \{9, 11\} = \{7, 13\}.\quad\halmos$$

(b) Take an element (it doesn't matter which one) from the coset, say $3 \in \{3, 17\}$ .

Perform the operation on the elements you chose. In this case, it's finding the inverse (use the Extended Euclidean Algorithm, or trial and error):

$$3^{-1} = 7.$$

Find the coset containing the answer: $7 \in \{7, 13\}$ .

Hence,

$$\{3, 17\}^{-1} = \{7, 13\}.\quad\halmos$$

(c) Take an element (it doesn't matter which one) from the coset, say $11 \in \{9, 11\}$ .

Perform the operation on the elements you chose. In this case, it's cubing:

$$11^3 = 1331 = 11.$$

Find the coset containing the answer: $11 \in \{9, 11\}$ .

Hence,

$$\{9, 11\}^3 = \{9, 11\}.\quad\halmos$$

(d) To save writing, I'll use $\overline{1}$ , $\overline{3}$ , $\overline{7}$ , and $\overline{9}$ to represent the cosets. I did the multiplications to construct the table the way I did the multiplication in (a) above.

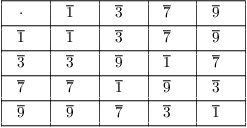
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & $\overline{1}$ & & $\overline{3}$ & & $\overline{7}$ & & $\overline{9}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\overline{1}$ & & $\overline{1}$ & & $\overline{3}$ & & $\overline{7}$ & & $\overline{9}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\overline{3}$ & & $\overline{3}$ & & $\overline{9}$ & & $\overline{1}$ & & $\overline{7}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\overline{7}$ & & $\overline{7}$ & & $\overline{1}$ & & $\overline{9}$ & & $\overline{3}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\overline{9}$ & & $\overline{9}$ & & $\overline{7}$ & & $\overline{3}$ & & $\overline{1}$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I can see that $\{3, 17\}$ has order 4. Therefore, $\dfrac{U_{20}}{\langle 19 \rangle} \approx \integer_4$ .

Example. The cosets of $\langle (1, 3) \rangle$ in $\integer_4 \times \integer_4$ are

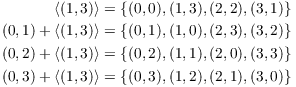
$$\eqalign{ \langle (1, 3) \rangle & = \{(0, 0), (1, 3), (2, 2), (3, 1)\} \cr (0, 1) + \langle (1, 3) \rangle & = \{(0, 1), (1, 0), (2, 3), (3, 2)\} \cr (0, 2) + \langle (1, 3) \rangle & = \{(0, 2), (1, 1), (2, 0), (3, 3)\} \cr (0, 3) + \langle (1, 3) \rangle & = \{(0, 3), (1, 2), (2, 1), (3, 0)\} \cr}$$

(a) Compute $[(0, 2) + \langle (1, 3)] + [(0, 3) + \langle (1, 3)]$ .

(b) Construct an addition table for the quotient group $\dfrac{\integer_4 \times \integer_4}{\langle (1, 3) \rangle}$ . Determine whether the quotient group is isomorphic to $\integer_4$ or to $\integer_2 \times \integer_2$ .

(a) Take an element (it doesn't matter which one) from the cosets, say $(0, 2) \in (0, 2) + \langle (1, 3)$ and $(0, 3) \in (0, 3) + \langle (1, 3)$ . (I'll just use the coset representatives, but again, I could choose any elements from the two cosets.)

Perform the operation on the elements you chose. In this case, it's addition:

$$(0, 2) + (0, 3) = (0, 1).$$

Find the coset containing the answer:

$$(0, 1) \in \{(0, 1), (1, 0), (2, 3), (3, 2)\} = (0, 1) + \langle (1, 3).$$

Hence,

$$[(0, 2) + \langle (1, 3)] + [(0, 3) + \langle (1, 3)] = (0, 1) + \langle (1, 3).\quad\halmos$$

(b) To save writing, I'll use $(0, 0)$ , $(0, 1)$ , $(0, 2)$ , and $(0, 3)$ to represent the cosets. I did the additions to construct the table the way I did the addition in (a) above.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 3)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 3)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 1)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 3)$ & & $(0, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 2)$ & & $(0, 2)$ & & $(0, 3)$ & & $(0, 0)$ & & $(0, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 3)$ & & $(0, 3)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

I can see that $(0, 1) + \langle (1, 3)$ has order 4, so $\dfrac{\integer_4 \times \integer_4}{\langle (1, 3) \rangle} \approx \integer_4$ .

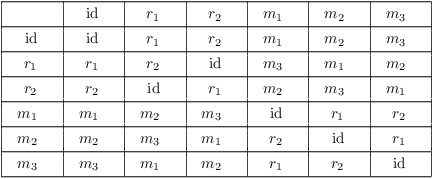
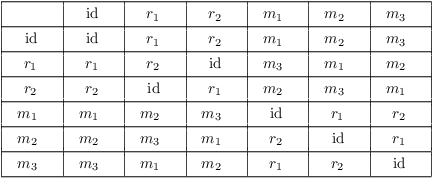
Example. ( A quotient group of a dihedral group) This is the table for $D_3$ , the group of symmetries of an equilateral triangle. $r_1$ is rotation through $\dfrac{2\pi}{3}$ , $r_2$ is rotation through $\dfrac{4\pi}{3}$ , and $m_1$ , $m_2$ , and $m_3$ are reflections through the altitude through vertices 1, 2, and 3, respectively.

$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfill \quad # \quad \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & && $\id$ && $r_1$ && $r_2$ && $m_1$ && $m_2$ && $m_3$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $\id$ && $\id$ && $r_1$ && $r_2$ && $m_1$ && $m_2$ && $m_3$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_1$ && $r_1$ && $r_2$ && $\id$ && $m_3$ && $m_1$ && $m_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_2$ && $r_2$ && $\id$ && $r_1$ && $m_2$ && $m_3$ && $m_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_1$ && $m_1$ && $m_2$ && $m_3$ && $\id$ && $r_1$ && $r_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_2$ && $m_2$ && $m_3$ && $m_1$ && $r_2$ && $\id$ && $r_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_3$ && $m_3$ && $m_1$ && $m_2$ && $r_1$ && $r_2$ && $\id$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} }} $$

(a) Show that the rotation subgroup $H = \{id, r_1, r_2\}$ is a normal subgroup of $D_3$ .

(b) Construct the multiplication table for the quotient group $D_3 / H$ and identify the quotient group as a familiar group.

(c) Consider the subgroup $H' = \{\id, m_1\}$ . Show that $H'$ is not normal in $D_3$ .

(a) Since H has 3 elements, it has index $\dfrac{6}{3} = 2$ , so it must be normal.

You can check this directly but tediously by checking that $g H g^{-1} \subset H$ for each $g \in D_3$ . For example,

$$m_1 H m_1^{-1} = m_1 H m_1 = m_1\{\id, r_1, r_2\}m_1 = \{m_1 \id m_1, m_1 r_1 m_1, m_1 r_2 m_1\} = \{\id, r_2, r_1\} = H.$$

And so on for the other elements.

It's also possible to show it's normal geometrically, by reasoning about orientation.

(b) $D_3/H$ is a group with two elements:

$$D_3/H = \{H = \{\id, \rho_1, \rho_2\}, m_1 H = \{m_1, m_2, m_3\}\}.$$

Here is the group table for $D_3 / H$ :

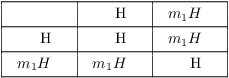
$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfill \quad # \quad \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit & \cr & & & H & & $m_1 H$ & \cr height2 pt & \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit & \cr & H & & H & & $m_1 H$ & \cr height2 pt & \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit & \cr & $m_1 H$ & & $m_1 H$ & & H & \cr height2 pt & \omit && \omit && \omit & \cr \noalign{\hrule} }} $$

Up to notation, this is "the" group of order 2, namely $\integer_2$ .

(More generally, consider the group $D_{2 n}$ of symmetries of the regular n-gon. This group has a subgroup of rotations H consisting of rotations through the angles $\dfrac{2\pi k}{n}$ , where $0 \le k < n$ . This subgroup is normal, since it has index 2. To see this geometrically, observe that if $\rho$ is a rotation and $\tau$ is also a rotation, $\tau \rho \tau^{-1}$ is obviously a rotation. On the other hand, suppose $\tau$ is a reflection. Then $\tau \rho \tau^{-1}$ is orientation-preserving, so it must also be a rotation.)

(c) I must find a $g \in D_3$ such that $gH'g^{-1} \ne H'$ . Here's an example:

$$m_2 \{\id, m_1\} m_2^{-1} = m_2 \{\id, m_1\} m_2 = \{m_2 \id m_2, m_2 m_1 m_2\} = \{\id, m_3\} \ne \{\id, m_1\}.$$

Another way to prove that the subgroup isn't normal is to compare the left and right cosets. The left cosets are

$$\{\id, m_1\}, m_2 \{\id, m_1\} = \{m_2, r_2\}, m_3 \{\id, m_1\} = \{m_3, r_1\}.$$

The right cosets are

$$\{\id, m_1\}, \{\id, m_1\} m_2 = \{m_2, r_1\}, \{\id, m_1\} m_3 = \{m_3, r_2\}.$$

As you can see, the left and right cosets are not the same.

Remember that when a subgroup is normal, there is a well-defined multiplication on the set of cosets of the subgroup. Let's see how this works out for the two subgroup I discussed above.

The first table below is the multiplication table for $D_3$ , the group of symmetries of a triangle. The subgroup $H = \{\id, r_1, r_2\}$ has two cosets: H itself and the set $\{m_1, m_2, m_3\}$ . Notice that the row and column headings have been set up with the two cosets one after another.

Get out your coloring pencils! Color the two cosets in the table below in such a way that all the elements of a given coset are the same color, and different cosets have different colors. For example, leave the elements of $H = \{\id, r_1, r_2\}$ uncolored and color the elements $\{m_1, m_2, m_3\}$ green.

$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfill \quad # \quad \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & && $\id$ && $r_1$ && $r_2$ && $m_1$ && $m_2$ && $m_3$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $\id$ && $\id$ && $r_1$ && $r_2$ && $m_1$ && $m_2$ && $m_3$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_1$ && $r_1$ && $r_2$ && $\id$ && $m_3$ && $m_1$ && $m_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_2$ && $r_2$ && $\id$ && $r_1$ && $m_2$ && $m_3$ && $m_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_1$ && $m_1$ && $m_2$ && $m_3$ && $\id$ && $r_1$ && $r_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_2$ && $m_2$ && $m_3$ && $m_1$ && $r_2$ && $\id$ && $r_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_3$ && $m_3$ && $m_1$ && $m_2$ && $r_1$ && $r_2$ && $\id$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} }} $$

Consider the product of two elements $ab$ . The coloring shows that the coset containing the product depends only on the cosets containing a and b. Suppose $ab$ is in the coset colored green. Take $a'$ in the same coset as a and $b'$ in the same coset as b. Then $a'b'$ will also be in the coset colored green. This proves that you can multiply cosets by multiplying coset representatives and get a well-defined multiplication.

Here is the same table rearranged to fit the non-normal subgroup $H' = \{\id, m_1\}$ and its cosets $r_1 H' = \{r_1, m_3\}$ and $r_2 H' = \{r_2, m_2\}$ . Color the elements of the three cosets with different colors as in the last example.

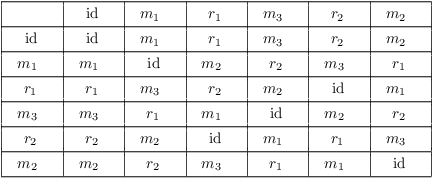
$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfill \quad # \quad \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & & & $\id$ & & $m_1$ & & $r_1$ & & $m_3$ & & $r_2$ & & $m_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $\id$ & & $\id$ & & $m_1$ & & $r_1$ & & $m_3$ & & $r_2$ & & $m_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_1$ & & $m_1$ & & $\id$ & & $m_2$ & & $r_2$ & & $m_3$ & & $r_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_1$ & & $r_1$ & & $m_3$ & & $r_2$ & & $m_2$ & & $\id$ & & $m_1$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_3$ & & $m_3$ & & $r_1$ & & $m_1$ & & $\id$ & & $m_2$ & & $r_2$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $r_2$ & & $r_2$ & & $m_2$ & & $\id$ & & $m_1$ & & $r_1$ & & $m_3$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr & $m_2$ & & $m_2$ & & $r_2$ & & $m_3$ & & $r_1$ & & $m_1$ & & $\id$ & \cr height2 pt & \omit && \omit && \omit && \omit && \omit && \omit && \omit & \cr \noalign{\hrule} }} $$

In this case, the coset containing a product $a \cdot b$ depends on the particular elements a and b, not just on the cosets containing a and b. The coloring produces a table that is not arranged in nice "blocks" like the previous table. For example, $r_1\cdot r_1 = r_2$ , which is in the third coset. On the other hand, $m_3\cdot m_3 = id$ , which is in the first coset. You get different cosets, even though the factors in the two products are all in the second coset. In this case, coset multiplication by multiplication of representatives is not well-defined.

It is natural to see how a new construction interacts with things like unions and intersections. Since the union of subgroups is not a subgroup in general, it's unreasonable to expect a union of normal subgroups to be a normal subgroup. However, intersections work properly.

Proposition. The intersection of a family of normal subgroups is a normal subgroup.

Proof. Let G be a group, and let $\{ H_a\}_{a \in A}$ be a family of normal subgroups of G. Let $H = \cap_{a \in A} H_a$ . I want to show that $H \triangleleft G$ . Since the intersection of a family of subgroups is a subgroup, it remains to show that H is normal.

Let $g \in G$ and let $h \in H$ . I must show $g h g^{-1} \in H$ . Now $h \in H$ implies $h \in H_a$ for all a, so (since $H_a \triangleleft G$ for all a) $g h g^{-1} \in H_a$ for all a. Therefore, $g h g^{-1} \in \cap_{a \in A} H_a = H$ . Therefore, H is normal.

Definition. Let G be a group, and let $S \subset G$ . The intersection of all normal subgroups of G containing S is the normal subgroup generated by S.

Why are normal subgroups and quotient groups important? The idea is that you might be able to understand groups by taking them apart into pieces, the way that you can factor a positive integer into a product of primes. If you're trying to understand a group G, you try to find a normal subgroup H. This allows you to decompose G into smaller groups H and $G/H$ . Now you try to find normal subgroups of H and of $G/H$ , and you keep going.

At some point, you may be unable to find any normal subgroups (other than $\{1\}$ and the group itself).

Definition. A group G is simple if its only normal subgroups are $\{1\}$ and G.

Thus, simple groups are to groups as prime numbers are to positive integers.

Proposition. Let $n \ge 2$ . Then n is prime if and only if $\integer_n$ is simple.

Proof. Suppose n is prime. The order of a subgroup must divide the order of the group (by Lagrange's theorem), and the only positive divisors of n are 1 and n. Therefore, the only subgroups --- and hence the only normal subgroups --- are $\{0\}$ and $\integer_n$ . Therefore, $\integer_n$ is simple.

Suppose n is composite. Then there is an integer m such that $m \mid n$ and $1 < m < n$ . Since $\integer_n$ is cyclic, it has a subgroup with m elements; since $\integer_n$ is abelian, that subgroup must be normal. Since $\integer_n$ has a normal subgroup other than $\{0\}$ and $\integer_n$ , it is not simple.

The hope is that if you know all the possible simple groups, and you know all the ways of putting them together, then you'll know all about groups. In its complete generality, this ideal is unattainable. However, progress has been made in this endeavor for finite groups. The finite simple groups were completely classified around 1980; estimates suggested that the complete proof (pieces of which were finished by many people over the course of decades) ran to thousands of pages.

There is a fundamental relationship between kernels of group maps and normal subgroups; in fact, normal subgroups are exactly the kernels of group maps. The first part of the next result proves part of this assertion.

Proposition. Let $f: G \rightarrow H$ be a group homomorphism.

(a) $\ker f \triangleleft G$ .

(b) If $H' \triangleleft H$ , then $f^{-1}(H') \triangleleft G$ .

Proof. (a) I showed earlier that $\ker f$ is a subgroup of G. So I only need to show that $\ker f$ is normal. Let $x \in \ker f$ (so $f(x) = 1$ ) and let $g \in G$ . I need to show that $g x g^{-1} \in \ker f$ .

$$f(g x g^{-1}) = f(g) f(x) f(g^{-1}) = f(g) f(g)^{-1} = 1.$$

Hence, $g x g^{-1} \in \ker f$ , and $\ker f \triangleleft G$ .

(b) I showed earlier that $f^{-1}(H')$ is a subgroup of G. I only need to show that if $H'$ is normal in H, then $f^{-1}(H')$ is normal in G.

Let $x \in f^{-1}(H')$ , so $f(x) \in H'$ , and let $g \in G$ . I must show that $g x g^{-1} \in f^{-1}(H')$ . Apply f and see if it winds up in $H'$ .

$$f(g x g^{-1}) = f(g) f(x) f(g^{-1}) = f(g) f(x) f(g)^{-1} \in f(g) H' f(g)^{-1} \subset H'.$$

(The last inclusion follows from normality of $H'$ .) Hence, $g x g^{-1} \in f^{-1}(H')$ , and $f^{-1}(H') \triangleleft G$ .

Remarks. (a) It's not true in general that the image of a normal subgroup is normal. It is true if the map is a surjection. (Try it yourself!)

(b) The lemma above says that kernels of group maps are normal subgroups. In fact, the converse is true, and I'll prove it later: Every normal subgroup is the kernel of a group map.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga