Direct Products

Definition. Let G and H be groups. The direct product $G \times H$ of G and H is the set of all ordered pairs $\{(g, h) \mid g \in G, h \in H\}$ with the operation

$$(g_1, h_1)\cdot (g_2, h_2) = (g_1 g_2, h_1 h_2).$$

\overfullrule=0pt

Remarks. 1. In the definition, I've assumed that G and H are using multiplication notation. In general, the notation you use in $G \times H$ depends on the notation in the factors. Examples:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & G & & H & & \hbox{\vbox{\hbox{Product}\vskip2 pt\hbox{($G \times H$)}}} & & \hbox{\vbox{\hbox{Identity}\vskip2 pt\hbox{($G \times H$)}}} & & \hbox{\vbox{\hbox{Inverse}\vskip2 pt\hbox{($G \times H$)}}} & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $g_1 \cdot g_2$ & & $h_1 \cdot h_2$ & & $(g_1, h_1)(g_2, h_2) = (g_1 g_2, h_1 h_2)$ & & $(1, 1)$ & & $(g, h)^{-1} = (g^{-1}, h^{-1})$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $g_1 + g_2$ & & $h_1 + h_2$ & & $(g_1, h_1) + (g_2, h_2) = (g_1 + g_2, h_1 + h_2)$ & & $(0, 0)$ & & $-(g, h) = (-g, -h)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $g_1 \cdot g_2$ & & $h_1 + h_2$ & & $(g_1, h_1)(g_2, h_2) = (g_1 g_2, h_1 + h_2)$ & & $(1, 0)$ & & $(g, h)^{-1} = (g^{-1}, -h)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

2. You can construct products of more than two groups in the same way. For example, if $G_1$ , $G_2$ , and $G_3$ are groups, then

$$G_1 \times G_2 \times G_3 = \{(x, y, z) \mid x \in G_1, y \in G_2, z \in G_3\}.$$

Just as with the two-factor product, you multiply elements componentwise.

Example. ( A product of cyclic groups which is cyclic) Show that $\integer_2 \times \integer_3$ is cyclic.

Since $\integer_2 = \{0, 1\}$ and $\integer_3 = \{0, 1, 2\}$ ,

$$\integer_2 \times \integer_3 = \{(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2)\}.$$

If you take successive multiples of $(1, 1)$ , you get

$$(1, 1), \quad (0, 2), \quad (1, 0), \quad (0, 1), \quad (1, 2), \quad (0, 0).$$

Since you can get the whole group by taking multiples of $(1, 1)$ , it follows that $\integer_2 \times \integer_3$ is actually cyclic of order 6 --- the same as $\integer_6$ .

Example. ( A product of cyclic groups which is not cyclic) Show that $\integer_2 \times \integer_2$ is not cyclic.

Since $\integer_2 = \{0, 1\}$ ,

$$\integer_2 \times \integer_2 = \{(0, 0), (1, 0), (0, 1), (1, 1)\}.$$

Here's the operation table:

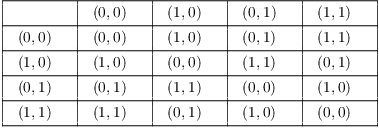
$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & $(0, 0)$ & & $(1, 0)$ & & $(0, 1)$ & & $(1, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & $(0, 0)$ & & $(1, 0)$ & & $(0, 1)$ & & $(1, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & $(1, 0)$ & & $(0, 0)$ & & $(1, 1)$ & & $(0, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 1)$ & & $(0, 1)$ & & $(1, 1)$ & & $(0, 0)$ & & $(1, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 1)$ & & $(1, 1)$ & & $(0, 1)$ & & $(1, 0)$ & & $(0, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Note that this is not the same group as $\integer_4$ . Both groups have 4 elements, but $\integer_4$ is cyclic of order 4. In $\integer_2 \times \integer_2$ , all the elements have order 2, so no element generates the group.

$\integer_2 \times \integer_2$ is the same as the Klein 4-group V, which has the following operation table:

$$\vbox{\offinterlineskip \halign{ & \vrule # & \strut \hfil \quad # \quad \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & 1 & & a & & b & & c & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & a & & b & & c & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & a & & 1 & & c & & b & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & b & & b & & c & & 1 & & a & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & c & & c & & b & & a & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

If G and H are finite, then $|G \times H| = |G||H|$ . (This is true for sets G and H; it has nothing to do with G and H being groups.) For example, $|\integer_5 \times \integer_6| = 30$ .

Lemma. The product of abelian groups is abelian: If G and H are abelian, so is $G \times H$ .

Proof. Suppose G and H are abelian. Let $(g, h), (g', h') \in G \times H$ , where $g, g' \in G$ and $h, h' \in H$ . I have

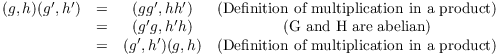
$$\matrix{(g, h)(g', h') & = & (g g', h h') & \hbox{(Definition of multiplication in a product)} \cr & = & (g' g, h' h) & \hbox{(G and H are abelian)} \cr & = & (g', h')(g, h) & \hbox{(Definition of multiplication in a product)} \cr}$$

This proves that $G \times H$ is abelian.

Remark. If either G or H is not abelian, then $G \times H$ is not abelian. Suppose, for instance, that G is not abelian. This means that there are elements $g_1, g_2 \in G$ such that

$$g_1 g_2 \ne g_2 g_1.$$

Then

$$(g_1, 1)(g_2, 1) = (g_1 g_2, 1), \quad\hbox{while}\quad (g_2, 1)(g_1, 1) = (g_2 g_1, 1).$$

Since $(g_1 g_2, 1) \ne (g_2 g_1, 1)$ , it follows that $(g_1, 1)(g_2, 1) \ne (g_2, 1)(g_1, 1)$ , so $G \times H$ is not abelian.

A similar argument works if H is not abelian.

Example. ( A product of an abelian and a nonabelian group) Construct the multiplication table for $\integer_2 \times D_3$ . (Recall that $D_3$ is the group of symmetries of an equilateral triangle.) The number of elements is

$$|\integer_2 \times D_3| = |\integer_2|\cdot |D_3| = 2 \cdot 6 = 12.$$

Here's the multiplication table for $\integer_2 \times D_3$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & (0, id) & & (0, $r_1$) & & (0, $r_2$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, id) & & (0, id) & & (0, $r_1$) & & (0, $r_2$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $r_1$) & & (0, $r_1$) & & (0, $r_2$) & & (0, id) & & (0, $m_3$) & & (0, $m_1$) & & (0, $m_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $r_2$) & & (0, $r_2$) & & (0, id) & & (0, id) & & (0, $m_2$) & & (0, $m_3$) & & (0, $m_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_1$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $m_3$) & & (0, id) & & (0, $r_1$) & & (0, $r_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_2$) & & (0, $m_2$) & & (0, $m_3$) & & (0, $m_1$) & & (0, $r_2$) & & (0, id) & & (0, $r_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_3$) & & (0, $m_3$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $r_1$) & & (0, $r_2$) & & (0, id) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, id) & & (1, id) & & (1, $r_1$) & & (1, $r_2$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $r_1$) & & (1, $r_1$) & & (1, $r_2$) & & (1, id) & & (1, $m_3$) & & (1, $m_1$) & & (1, $m_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $r_2$) & & (1, $r_2$) & & (1, id) & & (1, id) & & (1, $m_2$) & & (1, $m_3$) & & (1, $m_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_1$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $m_3$) & & (1, id) & & (1, $r_1$) & & (1, $r_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_2$) & & (1, $m_2$) & & (1, $m_3$) & & (1, $m_1$) & & (1, $r_2$) & & (1, id) & & (1, $r_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_3$) & & (1, $m_3$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $r_1$) & & (1, $r_2$) & & (1, id) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & (1, id) & & (1, $r_1$) & & (1, $r_2$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, id) & & (1, id) & & (1, $r_1$) & & (1, $r_2$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $r_1$) & & (1, $r_1$) & & (1, $r_2$) & & (1, id) & & (1, $m_3$) & & (1, $m_1$) & & (1, $m_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $r_2$) & & (1, $r_2$) & & (1, id) & & (1, id) & & (1, $m_2$) & & (1, $m_3$) & & (1, $m_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_1$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $m_3$) & & (1, id) & & (1, $r_1$) & & (1, $r_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_2$) & & (1, $m_2$) & & (1, $m_3$) & & (1, $m_1$) & & (1, $r_2$) & & (1, id) & & (1, $r_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (0, $m_3$) & & (1, $m_3$) & & (1, $m_1$) & & (1, $m_2$) & & (1, $r_1$) & & (1, $r_2$) & & (1, id) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, id) & & (0, id) & & (0, $r_1$) & & (0, $r_2$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $m_3$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $r_1$) & & (0, $r_1$) & & (0, $r_2$) & & (0, id) & & (0, $m_3$) & & (0, $m_1$) & & (0, $m_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $r_2$) & & (0, $r_2$) & & (0, id) & & (0, id) & & (0, $m_2$) & & (0, $m_3$) & & (0, $m_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_1$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $m_3$) & & (0, id) & & (0, $r_1$) & & (0, $r_2$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_2$) & & (0, $m_2$) & & (0, $m_3$) & & (0, $m_1$) & & (0, $r_2$) & & (0, id) & & (0, $r_1$) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & (1, $m_3$) & & (0, $m_3$) & & (0, $m_1$) & & (0, $m_2$) & & (0, $r_1$) & & (0, $r_2$) & & (0, id) & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The operation in $\integer_2$ is addition mod 2, while the operation in $D_3$ is written using multiplicative notation. When you multiply two pairs, you add in $\integer_2$ in the first component and multiply in $D_3$ in the second component:

$$(1, r_2)(1, m_2) = (1 + 1, r_2 \cdot m_2) = (0, m_3).$$

The identity is $(0,\hbox{id})$ , since 0 is the identity in $\integer_2$ , while id is the identity in $D_3$ .

$\integer_2 \times D_3$ is not abelian, since $D_3$ is not abelian. A particular example:

$$(1, m_2)(0, r_2) = (1, m_1), \quad\hbox{but}\quad (0, r_2)(1, m_2) = (1, m_3).\quad\halmos$$

Example. ( Using products to construct groups) Use products to construct 3 different abelian groups of order 8. The groups $\integer_2 \times \integer_2 \times \integer_2$ , $\integer_4 \times \integer_2$ , and $\integer_8$ are abelian, since each is a product of abelian groups. $\integer_8$ is cyclic of order 8, $\integer_4 \times \integer_2$ has an element of order 4 but is not cyclic, and $\integer_2 \times \integer_2 \times \integer_2$ has only elements of order 2. It follows that these groups are distinct.

In fact, there are 5 distinct groups of order 8; the remaining two are nonabelian.

The group $D_4$ of symmetries of the square is a nonabelian group of order 8.

The fifth (and last) group of order 8 is the group Q of the quaternions.

$D_4$ or Q are not that same as $\integer_2 \times \integer_2 \times \integer_2$ , $\integer_4 \times \integer_2$ , or $\integer_8$ , since $\integer_2 \times \integer_2 \times \integer_2$ , $\integer_4 \times \integer_2$ , and $\integer_8$ are abelian while $D_4$ or Q are not.

Finally, $D_4$ is not the same as Q. $D_4$ has 5 elements of order 2: The four reflections and rotation through $180^\circ$ . Q has one element of order 2, namely -1.

I've shown that these five groups of order 8 are distinct; it takes considerably more work to show that these are the only groups of order 8.

Definition. Let m and n be positive integers. The least common multiple $[m, n]$ of m and n is the smallest positive integer divisible by m and n.

Remark. Since $m n$ is divisible by m and n, the set of positive multiples of m and n is nonempty. Hence, it has a smallest element, by well-ordering. It follows that the least common multiple of two positive integers is always defined. For example, $[18, 30] = 90$ .

Lemma. If s is a common multiple of m and n, then $[m, n] \mid s$ .

Proof. By the Division Algorithm,

$$s = q \cdot [m, n] + r, \quad\hbox{where}\quad 0 \le r < [m, n].$$

Thus, $r = s - q \cdot [m, n]$ . Since $m \mid s$ and $m \mid [m, n]$ , I have $m \mid r$ . Since $n \mid s$ and $n \mid [m, n]$ , I have $n \mid r$ . Therefore, r is a common multiple of m and n. Since it's also less than the least common multiple $[m, n]$ , it can't be positive. Therefore, $r = 0$ , and $s = q \cdot [m, n]$ , i.e. $[m, n] \mid s$ .

Remark. The lemma shows that the least common multiple is not just "least" in terms of size. It's also "least" in the sense that it divides every other common multiple.

Theorem. Let m and n be positive integers. Then

$$m n = (m, n) [m, n].$$

Proof. I'll prove that each side is greater than or equal to the other side.

Note that $\dfrac{m}{(m, n)}$ and $\dfrac{n}{(m, n)}$ are integers. Thus,

$$\dfrac{m n}{(m, n)} = m \cdot \dfrac{n}{(m, n)} = \dfrac{m}{(m, n)} \cdot n.$$

This shows that $\dfrac{m n}{(m, n)}$ is a multiple of m and a multiple of n. Therefore, it's a common multiple of m and n, so it must be greater than or equal to the least common multiple. Hence,

$$\dfrac{m n}{(m, n)} \ge [m, n], \quad\hbox{and}\quad m n \ge (m, n)[m, n].$$

Next, $[m, n]$ is a multiple of n, so $[m, n] = s n$ for some s. Then

$$\dfrac{m n}{[m, n]} = \dfrac{m n}{s n} = \dfrac{m}{s} \mid m.$$

(Why is $\dfrac{m n}{[m, n]}$ an integer? Well, $m n$ is a common multiple of m and n, so by the previous lemma $[m, n] \mid m n$ .)

Similarly, $[m, n]$ is a multiple of m, so $[m, n] = t m$ for some t. Then

$$\dfrac{m n}{[m, n]} = \dfrac{m n}{t m} = \dfrac{n}{t} \mid n.$$

In other words, $\dfrac{m n}{[m, n]}$ is a common divisor of m and n. Therefore, it must be less than the greatest common divisor:

$$\dfrac{m n}{[m, n]} \le (m, n), \quad\hbox{and}\quad m n \le (m, n)[m, n].$$

The two inequalities I've proved show that $m n = (m, n)[m, n]$ .

Example. Verify that $m n = (m, n) [m, n]$ if $m = 54$ and $n = 72$ .

$(54, 72) = 18$ , $[54, 72] = 216$ , and

$$(54, 72) [54, 72] = 18 \cdot 216 = 3888 = 54 \cdot 72.\quad\halmos$$

Proposition. The element $(1, 1)$ has order $[m, n]$ in $\integer_m \times \integer_n$ .

Proof.

$$[m, n](1, 1) = ([m, n], [m, n]).$$

The first component is 0, since it's divisible by m; the second component is 0, since it's divisible by n. Hence, $[m, n](1, 1) = (0, 0)$ .

Next, I must show that $[m, n]$ is the smallest positive multiple of $(1, 1)$ which equals the identity. Suppose $k(1, 1) = (0, 0)$ , so $(k, k) = (0, 0)$ . Consider the first components. $k = 0$ in $\integer_m$ means that $m \mid k$ ; likewise, the second components show that $n \mid k$ . Since k is a common multiple of m and n, it must be greater than or equal to the least common multiple $[m, n]$ : that is, $k \ge [m, n]$ . This proves that $[m, n]$ is the order of $(1, 1)$ .

Example. Find the order of $(1, 1)$ in $\integer_4 \times \integer_6$ . Find the order of $(1, 1) \in \integer_5 \times \integer_6$ .

The element $(1, 1)$ has order $[4, 6] = 12$ .

On the other hand, the element $(1, 1) \in \integer_5 \times \integer_6$ has order $[5, 6] = 30$ . Since $\integer_5 \times \integer_6$ has order 30, the group is cyclic; in fact, $\integer_5 \times \integer_6 \approx \integer_{30}$ .

Remark. More generally, consider $(x_1, \ldots, x_n) \in G_1 \times \ldots \times G_n$ , and suppose $x_i$ has order $r_i$ in $G_i$ . (The $G_i$ 's need not be cyclic.) Then $(x_1, \ldots, x_n)$ has order $[r_1, \ldots, r_n]$ .

Corollary. $\integer_m \times \integer_n$ is cyclic of order $m n$ if and only if $(m, n) = 1$ .

Note: In the next proof, "$(a, b)$ " may mean either the ordered pair $(a, b)$ or the greatest common divisor of a and b. You'll have to read carefully and determine the meaning from the context.

Proof. If $(m, n) = 1$ , then $[m, n] = m n$ . Thus, the order of $(1, 1)$ is $[m, n] = m n$ . But $\integer_m \times \integer_n$ has order $mn$ , so $(1, 1)$ generates the group. Hence, $\integer_m \times \integer_n$ is cyclic.

Suppose on the other hand that $(m, n) \ne 1$ . Since $(m, n)[m, n] = m n$ , it follows that $[m, n] \ne m n$ . Since $m n$ is a common multiple of m and n and since $[m, n]$ is the least common multiple, it follows that $[m, n] < m n$ .

Now consider an element $(a, b) \in \integer_m \times \integer_n$ . Let p be the order of a in $\integer_m$ and let q be the order of b in $\integer_n$ .

Since $p \mid m \mid [m, n]$ , I may write $p j = [m, n]$ for some j. Since $q \mid n \mid [m, n]$ , I may write $q k = [m, n]$ for some k. Then

$$[m, n] (a, b) = ([m, n] a, [m, n] b) = (j(p a), k(q b)) = (j \cdot 0, k \cdot 0) = (0, 0).$$

Hence, the order of $(a, b)$ is less than or equal to $[m, n]$ . But $[m, n] < m n$ , so the order of $(a, b)$ is less than (and not equal to) $m n$ .

Since $(a, b)$ was an arbitrary element of $\integer_m \times \integer_n$ , it follows that no element of $\integer_m \times \integer_n$ has order $m n$ . Therefore, $\integer_m \times \integer_n$ can't be cyclic of order $m n$ , since a generator would have order $m n$ .

Remark. More generally, if $m_1$ , ..., $m_k$ are pairwise relatively prime, then $\integer_{m_1} \times \ldots \times \integer_{m_k}$ is cyclic of order $m_1 \cdots m_k$ .

Example. ( Orders of elements in products) Find the order of $(2, 4, 4) \in \integer_4 \times \integer_{12} \times \integer_6$ .

2 has order 2 in $\integer_4$ , 4 has order 3 in $\integer_{12}$ , and 4 has order 3 in $\integer_6$ . Hence, the order of $(2, 4, 4)$ is $[2, 3, 3] = 6$ .

Example. ( A product of cyclic groups which is not cyclic) Prove directly that $\integer_2 \times \integer_4$ is not cyclic of order 8.

If $(a, b) \in \integer_2 \times \integer_4$ , then

$$4(a, b) = (4 a, 4 b) = (0, 0).$$

Thus, every element of $\integer_2 \times \integer_4$ has order less than or equal to 4. In particular, there can be no elements of order 8, i.e. no cyclic generators.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga