The Quotient Field of an Integral Domain

The rationals $\rational$ are constructed from the integers $\integer$ by "forming fractions". This amounts to making all the nonzero elements of $\integer$ invertible. In fact, you can perform this construction for an arbitrary integral domain.

Theorem. Let R be an integral domain.

(a) There is a field Q, the quotient field of R, and an injective ring map $i: R \rightarrow Q$ .

(b) If F is a field and $\phi: R \rightarrow F$ is an injective ring map, there is a unique ring map $\tilde\phi: Q \rightarrow F$ such that the following diagram commutes:

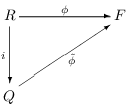
$$\commdiag{ R & \mapright^\phi & F \cr \mapdown\lft{i} & \arrow(3,2)\rt{\tilde\phi} & \cr Q & & \cr}$$

Heuristically, this means that Q is the "minimal" way of inverting the nonzero elements of R.

Proof. The first step is to form the fractions. Let

$$S = \{(a,b) \mid a, b \in R, b \ne 0\}.$$

(Think of $(a, b)$ as corresponding to the fraction $\dfrac{a}{b}$ . The elements of Q aren't actually fractions, but equivalence classes of fractions. Think of the situation in the rationals $\rational$ : $\dfrac{1}{2}$ and $\dfrac{2}{4}$ are really the same element of $\rational$ .)

Two rational fractions $\dfrac{a}{b}$ and $\dfrac{c}{d}$ are equal if and only if $a d = b c$ . I'll use this idea to put an equivalence relation on S.

If $(a, b), (c, d) \in S$ , write $(a, b) \sim (c, d)$ if and only if $a d = b c$ . I claim this is an equivalence relation.

(a) Since $a b = a b$ , I have $(a, b) = (a, b)$ .

(b) If $(a, b) \sim (c, d)$ , then $a d = b c$ . So $b c = a d$ , and hence $(c, d) \sim (a, b)$ .

(c) Suppose $(a, b) \sim (c, d)$ and $(c, d) \sim (e, f)$ . Then $a d = b c$ and $c f = d e$ . I want to show that $a f = b e$ . The first equation yields $a d f = b c f$ , while the second equation yields $b c f = b d e$ . Therefore, $a d f = b d e$ . Now $(c, d) \in S$ implies $d \ne 0$ , and since R is a domain, I may cancel d to obtain $a f = b e$ . Hence, $(a, b) = (e, f)$ , which completes the proof of transitivity.

Let Q be the set of equivalence classes. Let $[a, b] \in Q$ denote the equivalence class of $(a, b) \in S$ . I want to show that Q is a field with the appropriate properties.

First, I'll define the operations. For $[a, b], [c, d] \in Q$ , define

$$\eqalign{ [a, b] + [c, d] & = [a d + b c, b d] \cr [a, b] [c, d] & = [a c, b d] \cr}$$

Note that in each case $b, d \ne 0$ so $b d \ne 0$ , and the expressions on the right at least make sense.

I now have some routine but extremely tedious verifications to perform. Since these operations are defined on equivalence classes, I must check that they're well-defined --- i.e. that they're independent of the choices of representatives for the equivalence classes.

Once I have well-defined operations, I have to check all the axioms for a field. This entails checking all the ring axioms, commutativity, and the existence of inverses for nonzero elements. For example, I'll show that $[0, 1]$ functions as an additive identity, while $[1, 1]$ is the multiplicative identity.

It is probably a little much to expect you to wade through all of the ugly computations. Nevertheless, I'll show all the work below. I suggest that you at least verify that one of the two operations is well-defined, and that you work through the proof for at least one of the ring axioms.

First, I'll prove that addition and multiplication are well-defined. Suppose that $[a, b] = [a', b']$ , so $a b' = a' b$ , and $[c, d] = [c', d']$ so $c d' = c' d$ .

1. Addition is well-defined.

$$[a, b] + [c, d] = [a d + b c, b d] \quad\hbox{and}\quad [a', b'] + [c', d'] = [a' d' + b' c', b' d'].$$

Now

$$(a d + b c) b' d' = a b' d d' + b b' c d' = a' b d d' + b b' c' d = (a' d' + b' c') b d,$$

Hence, $[a d + b c, b d] = [a' d' + b' c', b' d']$ .

2. Multiplication is well-defined.

$$[a, b] [c, d] = [a c, b d] \quad\hbox{and}\quad [a', b'] [c', d'] = [a' c', b' d'].$$

Now

$$(a c)(b' d') = a b' c d' = a' b c' d = (a' c')(b d).$$

Hence, $[a c, b d] = [a' c', b' d']$ .

Next, I'll verify that Q is a field. I have to verify the ring axioms, that multiplication is commutative, and that nonzero elements have inverses.

3. Addition is associative.

$$\left([a, b] + [c, d]\right) + [e, f] = [a d + b c, b d] + [e, f] = [a d f + b c f + b d e, b d f],$$

$$[a, b] + \left([c, d] + [e, f]\right) = [a, b] + [c f + d e, d f] = [a d f + b c f + b d e, b d f].$$

4. Addition is commutative.

$$[a, b] + [c, d] = [a d + b c, b d] \quad\hbox{and}\quad [c, d] + [a, b] = [b c + a d, b d].$$

5. $[0, 1]$ is the additive identity.

$$[a, b] + [0, 1] = [a \cdot 1 + b \cdot 0, b] = [a, b].$$

6. $-[a, b] = [-a, b]$ .

$$[a, b] + [-a, b] = [a b - a b, b^2] = [0, b^2].$$

However, $[0, b^2] = [0, 1]$ , since $0\cdot 1 = b^2\cdot 0$ .

7. Multiplication is associative.

$$\left([a, b] [c, d]\right) [e, f] = [a c e, b d f] = [a, b] \left([c, d] [e, f]\right).$$

8. Multiplication is commutative.

$$[a, b] [c, d] = [a c, b d] = [c, d] [a, b].$$

9. $[1, 1]$ is the multiplicative identity.

$$[a, b] [1, 1] = [a, b].$$

10. Multiplication distributes over addition.

By commutativity of multiplication, it suffices to check this on one side.

$$[a, b]\left([c, d] + [e, f]\right) = [a, b] [c f + d e, d f] = [a c f + a d e, b d f],$$

$$[a, b] [c, d] + [a, b] [e, f] = [a c, b d] + [a e, b f] = [a b c f + a b d e, b^2 d f].$$

However,

$$(a c f + a d e) b^2 d f = a b^2 c d f^2 + a b^2 d^2 e f \quad\hbox{and}\quad (a b c f + a b d e) b d f = a b^2 c d f^2 + a b^2 d^2 e f.$$

Therefore, $[a c f + a d e, b d f] = [a b c f +a b d e, b^2 d f]$ .

11. Nonzero elements have multiplicative inverses.

Suppose $[a, b] \ne [0, 1]$ , so $a \ne 0$ . Then using $a b \cdot 1 = 1 \cdot a b$ , I have

$$[a, b] [b, a] = [a b, a b] = [1, 1].$$

Hence, $[b, a] = [a, b]^{-1}$ .

This completes the verification that Q is a field. Next, I'll construct the imbedding of R into Q.

Define $i: R \rightarrow Q$ by $i(r) = [r, 1]$ . I'll check that i is a ring map. First, $i(1) = [1, 1]$ .

Next,

$$i(a) + i(b) = [a, 1] + [b, 1] = [a + b, 1] = i(a + b),$$

$$i(a)i(b) = [a, 1] [b, 1] = [ab, 1] = i(ab).$$

Next, I'll show that i is injective. Suppose $i(x) = [0, 1]$ (since $[0, 1]$ is the zero element of Q). Then $[x, 1] = [0, 1]$ , or $x = 0$ . Therefore, $\ker i = \{ 0\}$ , so i is injective.

Finally, I'll complete the proof by verifying the universal property. Suppose that F is a field and $\phi: R \rightarrow F$ is an injective ring map. Define $\tilde{\phi}: Q \rightarrow F$ by

$$\tilde{\phi}\left([a, b]\right) = \phi(a)\phi(b)^{-1}.$$

Observe that since $b \ne 0$ , $\phi(b) \ne 0$ (injectivity), so $\phi(b)$ is invertible in the field F.

I have to check that the map is well-defined. Suppose that $[a, b] = [a', b']$ , so $a b' = a' b$ . Then

$$\eqalign{ \phi(a) \phi(b') & = \phi(a') \phi(b),\cr \phi(a) \phi(b)^{-1} & = \phi(a') \phi(b')^{-1},\cr \tilde{\phi}\left([a, b]\right) & = \tilde{\phi}\left([a', b']\right).}$$

Next, I'll check that $\tilde{\phi}$ is a ring map. First,

$$\tilde{\phi}\left([1, 1]\right) = \phi(1) \phi(1)^{-1} = 1 \cdot 1 = 1.$$

Next,

$$\tilde{\phi}\left([a, b] + [c, d]\right) = \tilde{\phi}\left([a d + b c, b d]\right) = \phi(a d + b c) \phi(b d)^{-1} = \phi(a d) \phi(b d)^{-1} + \phi(b c) \phi(b d)^{-1} =$$

$$\phi(a) \phi(d) \phi(b)^{-1} \phi(d)^{-1} + \phi(b) \phi(c) \phi(b)^{-1} \phi(d)^{-1} = \phi(a) \phi(b)^{-1} + \phi(c) \phi(d)^{-1} = \tilde{\phi}\left([a, b]\right) + \tilde{\phi}\left([c, d]\right).$$

Finally,

$$\tilde{\phi}\left([a, b] [c, d]\right) = \tilde{\phi}\left([a c, b d]\right) = \phi(a c) \phi(b d)^{-1} = \phi(a) \phi(b)^{-1} \phi(c) \phi(d)^{-1} = \tilde{\phi}\left([a, b]\right)\tilde{\phi}\left([c, d]\right).$$

I need to check that $\tilde{\phi}$ makes the diagram commute. If $a \in R$ ,

$$\tilde{\phi} \cdot i(a) = \tilde{\phi}\left([a, 1]\right) = \phi(a) \phi(1)^{-1} = \phi(a).$$

Finally, I'll show that $\tilde{\phi}$ is the only map which could satisfy these conditions. If $\psi$ was another injective ring map filling in the diagram, then for $a \in R$ ,

$$\psi \cdot i(a) = \phi(a).$$

Hence, $\psi\left([a, 1]\right) = \phi(a)$ .

Now let $b \in R$ , $b \ne 0$ . Since $\psi$ is a ring map,

$$1 = \psi\left([1, 1]\right) = \psi\left([b, 1] [1, b]\right) = \psi\left([b, 1]\right) \psi\left([1, b]\right) = \phi(b) \psi\left([1, b]\right).$$

$\phi$ is injective, so $\phi(b) \ne 0$ , and it's invertible in F. Therefore, $\psi\left([1, b]\right) = \phi(b)^{-1}$ .

Now put the results of the last two paragraphs together, again using the fact that $\psi$ is a ring map:

$$\psi\left([a, b]\right) = \psi\left([a, 1] [1, b]\right) = \psi\left([a, 1]\right) \psi\left([1, b]\right) = \phi(a) \phi(b)^{-1} = \tilde{\phi}\left([a, b]\right).$$

Thus, $\tilde{\phi}$ is the unique map filling in the diagram, and the proof is (finally!) complete.

The standard argument for objects defined by universal properties shows that the quotient field of an integral domain is unique up to ring isomorphism. That is, if R is a domain and Q and $Q'$ are fields satisfying the universal property for the quotient field of R, then $Q \approx Q'$ .

If R is a field, then it is its own quotient field. To prove this, use uniqueness of the quotient field, and the fact that the identity map $\hbox{id}: R \rightarrow R$ satisfies the universal property.

In most cases, it is easy to see what the quotient field "looks like". For example, let R be the domain $\rational[x]$ of polynomials with rational coefficients. The quotient field is $\rational(x)$ , the field of rational functions with rational coefficients. It consists of all quotients $\dfrac{p(x)}{q(x)}$ , where $p, q \in \rational[x]$ and $q \ne 0$ , under the usual operations.

This may seem like a lot of work to produce something that is "obvious". But the reason this may seem "obvious" to you is that you've had lots of experience working with the the rational numbers $\rational$ , the quotient field of the integers $\integer$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga