Quotient Rings

Let R be a ring, and let I be a (two-sided) ideal. Considering just the operation of addition, R is a group and I is a subgroup. In fact, since R is an abelian group under addition, I is a normal subgroup, and the quotient group $\dfrac{R}{I}$ is defined. Addition of cosets is defined by adding coset representatives:

$$(a + I) + (b + I) = (a + b) + I.$$

The zero coset is $0 + I = I$ , and the additive inverse of a coset is given by $-(a + I) = (-a) + I$ .

However, R also comes with a multiplication, and it's natural to ask whether you can turn $\dfrac{R}{I}$ into a ring by multiplying coset representatives:

$$(a + I)\cdot (b + I) = ab + I.$$

I need to check that that this operation is well-defined, and that the ring axioms are satisfied. In fact, everything works, and you'll see in the proof that it depends on the fact that I is an ideal. Specifically, it depends on the fact that I is closed under multiplication by elements of R.

By the way, I'll sometimes write "$\dfrac{R}{I}$ " and sometimes "$R/I$ "; they mean the same thing.

Theorem. If I is a two-sided ideal in a ring R, then $R/I$ has the structure of a ring under coset addition and multiplication.

Proof. Suppose that I is a two-sided ideal in R. Let $r, s \in I$ .

Coset addition is well-defined, because R is an abelian group and I a normal subgroup under addition. I proved that coset addition was well-defined when I constructed quotient groups.

I need to show that coset multiplication is well-defined:

$$(r + I)(s + I) = r s + I.$$

As before, suppose that

$$r + I = r' + I, \quad\hbox{so}\quad r = r' + a, \quad a \in I$$

$$s + I = s' + I, \quad\hbox{so}\quad s = s' + b, \quad b \in I$$

Then

$$(r + I)(s + I) = rs + I = (r' + a)(s' + b) + I = r' s' + r' b + a s' + a b + I = r' s' + I = (r' + I)(s' + I).$$

The next-to-last equality is derived as follows: $r' b + a s' + a b \in I$ , because I is an ideal; hence $r' b + a s' + a b + I = I$ . Note that this uses the multiplication axiom for an ideal; in a sense, it explains why the multiplication axiom requires that an ideal be closed under multiplication by ring elements on the left and right.

Thus, coset multiplication is well-defined.

Verification of the ring axioms is easy but tedious: It reduces to the axioms for R.

For instance, suppose I want to verify associativity of multiplication. Take $r, s, t \in R$ . Then

$$\left((r + I)(s + I)\right)(t + I) = (r s + I)(t + I) = (r s)t + I = r(s t) + I = (r + I)(s t + I) = (r + I) \left((s + I) (t + I)\right).$$

(Notice how I used associativity of multiplication in R in the middle of the proof.) The proofs of the other axioms are similar.

Definition. If R is a ring and I is a two-sided ideal, the quotient ring of R mod I is the group of cosets $\dfrac{R}{I}$ with the operations of coset addition and coset multiplication.

Proposition. Let R be a ring, and let I be an ideal

(a) If R is a commutative ring, so is $R/I$ .

(b) If R has a multiplicative identity 1, then $1 + I$ is a multiplicative identity for $R/I$ . In this case, if $r \in R$ is a unit, then so is $r + I$ , and $(r + I)^{-1} = r^{-1} + I$ .

Proof. (a) Let $r + I, s + I \in R/I$ . Since R is commutative,

$$(r + I)(s + I) = rs + I = sr + I = (s + I)(r + I).$$

Therefore, $R/I$ is commutative.

(b) Suppose R has a multiplicative identity 1. Let $r \in R$ . Then

$$(r + I)(1 + I) = r\cdot 1 + I = r + I \quad\hbox{and}\quad (1 + I)(r + I) = 1\cdot r + I = r + I.$$

Therefore, $1 + I$ is the identity of $R/I$ .

If $r \in R$ is a unit, then

$$(r^{-1} + I)(r + I) = r^{-1} r + I = 1 + I \quad\hbox{and}\quad (r + I)(r^{-1} + I) = r r^{-1} + I = 1 + I.$$

Therefore, $(r + I)^{-1} = r^{-1} + I$ .

Example. ( A quotient ring of the integers) The set of even integers $\langle 2 \rangle = 2 \integer$ is an ideal in $\integer$ . Form the quotient ring $\dfrac{\integer}{2 \integer}$ .

Construct the addition and multiplication tables for the quotient ring.

Here are some cosets:

$$2 + 2 \integer, \quad -15 + 2 \integer, \quad 841 + 2 \integer.$$

But two cosets $a + 2 \integer$ and $b + 2 \integer$ are the same exactly when a and b differ by an even integer. Every even integer differs from 0 by an even integer. Every odd integer differs from 1 by an even integer. So there are really only two cosets (up to renaming): $0 + 2 \integer = 2 \integer$ and $1 + 2 \integer$ .

Here are the addition and multiplication tables:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & + & & $0 + 2 \integer$ & & $1 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $0 + 2 \integer$ & & $0 + 2 \integer$ & & $1 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $1 + 2 \integer$ & & $1 + 2 \integer$ & & $0 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.5 in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $\times$ & & $0 + 2 \integer$ & & $1 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $0 + 2 \integer$ & & $0 + 2 \integer$ & & $0 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $1 + 2 \integer$ & & $0 + 2 \integer$ & & $1 + 2 \integer$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

You can see that $\dfrac{\integer}{2 \integer}$ is isomorphic to $\integer_2$ .

In general, $\dfrac{\integer}{n \integer}$ is isomorphic to $\integer_n$ . I've been using "$\integer_n$ " informally to mean the set $\{0, 1, \ldots, n - 1\}$ with addition and multiplication mod n, and taking for granted that the usual ring axioms hold. This example gives a formal contruction of $\integer_n$ as the quotient ring $\dfrac{\integer}{n \integer}$ .

Example. $\integer_3[x]$ is the ring of polynomials with coefficients in $\integer_3$ . Consider the ideal $\langle 2 x^2 + x + 2\rangle$ .

(a) How many elements are in the quotient ring $\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ ?

(b) Reduce the following product in $\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ to the form $(a x + b) + \langle 2 x^2 + x + 2\rangle$ :

$$(2 x + 1 + \langle 2 x^2 + x + 2\rangle) \cdot (x + 1 + \langle 2 x^2 + x + 2\rangle).$$

(c) Find $[x + 2 + \langle 2 x^2 + x + 2 \rangle]^{-1}$ in$\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ .

The ring $\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ is analogous to $\integer_n = \dfrac{\integer}{\langle n \rangle}$ . In the case of $\integer_n$ , you do computations mod n: To "simplify", you divide the result of a computation by the modulus n and take the remainder. In $\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ , the polynomial $2 x^2 + x + 2$ acts like the "modulus". To do computations in $\dfrac{\integer_3[x]}{\langle 2 x^2 + x + 2\rangle}$ , you divide the result of a computation by $2 x^2 + x + 2$ and take the remainder.

(a) By the Division Algorithm, any $f(x) \in \integer_3[x]$ can be written as

$$f(x) = (2 x^2 + x + 2) q(x) + r(x), \quad\hbox{where}\quad \deg r(x) < \deg (2 x^2 + x + 2).$$

This means that $r(x) = a x + b$ , where $a, b \in \integer_3$ . Then

$$f(x) + \langle 2 x^2 + x + 2\rangle = [(2 x^2 + x + 2) q(x) + r(x)] + \langle 2 x^2 + x + 2\rangle = (a x + b) + \langle 2 x^2 + x + 2\rangle.$$

Since there are 3 choices for a and 3 choices for b, there are 9 cosets.

(b) First, multiply the coset representatives:

$$(2 x + 1)(x + 1) = 2 x^2 + 1.$$

Dividing $2 x^2 + 1$ by $2 x^2 + x + 2$ , I get

$$2 x^2 + 1 = (2 x^2 + x + 2)(1) + (2 x + 2).$$

Then

$$2 x^2 + 1 + \langle 2 x^2 + x + 2 \rangle = [(2 x^2 + x + 2)(1) + (2 x + 2)] + \langle 2 x^2 + x + 2 \rangle = 2 x + 2 + \langle 2 x^2 + x + 2 \rangle.\quad\halmos$$

(c) To find multiplicative inverses in $\integer_n$ , you use the Extended Euclidean Algorithm. The same idea works in quotient rings of polynomial rings.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $2 x^2 + x + 2$ & & - & & $2 x$ & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & $x + 2$ & & $2 x$ & & 1 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & \cr & 2 & & $2 x + 1$ & & 0 & \cr height2 pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

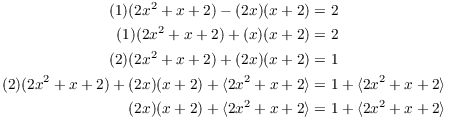
$$\eqalign{ (1)(2 x^2 + x + 2) - (2 x)(x + 2) & = 2 \cr (1)(2 x^2 + x + 2) + (x)(x + 2) & = 2 \cr (2)(2 x^2 + x + 2) + (2 x)(x + 2) & = 1 \cr (2)(2 x^2 + x + 2) + (2 x)(x + 2) + \langle 2 x^2 + x + 2 \rangle & = 1 + \langle 2 x^2 + x + 2 \rangle\cr (2 x)(x + 2) + \langle 2 x^2 + x + 2 \rangle & = 1 + \langle 2 x^2 + x + 2 \rangle\cr}$$

Thus,

$$[x + 2 + \langle 2 x^2 + x + 2 \rangle]^{-1} = 2 x + \langle 2 x^2 + x + 2 \rangle.\quad\halmos$$

Example. (a) List the elements of the cosets of $\langle (2, 2) \rangle$ in the ring $\integer_4 \times \integer_6$ .

(b) Is the quotient ring $\dfrac{\integer_4 \times \integer_6}{\langle (2, 2) \rangle}$ an integral domain?

(a) If x is an element of a ring R, the ideal $\langle x \rangle$ consists of all multiples of x by elements of R. It is not necessarily the same as the additive subgroup generated by x, which is

$$\{\ldots, -3 x, -2 x, -x, 0, x, 2 x, 3 x, \ldots\}.$$

In this example, the additive subgroup generated by $(2, 2)$ is

$$\{(0, 0), (2, 2), (0, 4), (2, 0), (0, 2), (2, 4)\}.$$

As usual, I get it by starting with the zero element $(0, 0)$ and the generator $(2, 2)$ , then adding $(2, 2)$ until I get back to $(0, 0)$ .

This set is contained in the ideal $\langle (2, 2) \rangle$ ; I need to check whether it is the same as the ideal.

If $(a, b) \in \integer_4 \times \integer_6$ , then

$$(a, b) \cdot (2, 2) = (2 a, 2 b).$$

Thus, an element of the ideal $\langle (2, 2) \rangle$ consists of a pair $(2 a, 2 b)$ , where each component is even. There are two even elements in $\integer_4$ (namely 0 and 2) and 3 even elements in $\integer_6$ (namely 0, 2, and 4), so there are $2 \cdot 3 = 6$ such pairs. Thus, the ideal $\langle (2, 2) \rangle$ has a maximum of 6 elements. Since the additive subgroup above already has 6 elements, it must be the same as the ideal.

I can list the elements of the cosets of the ideal as I would for subgroups.

$$\eqalign{ \langle (2, 2) \rangle & = \{(0, 0), (2, 2), (0, 4), (2, 0), (0, 2), (2, 4)\} \cr (0, 1) + \langle (2, 2) \rangle & = \{(0, 1), (2, 3), (0, 5), (2, 1), (0, 3), (2, 5)\} \cr (1, 0) + \langle (2, 2) \rangle & = \{(1, 0), (3, 2), (1, 4), (3, 0), (1, 2), (3, 4)\} \cr (1, 1) + \langle (2, 2) \rangle & = \{(1, 1), (3, 3), (1, 5), (3, 1), (1, 3), (3, 5)\} \cr}\quad\halmos$$

(b) Note that

$$[(0, 1) + \langle (2, 2) \rangle][(1, 0) + \langle (2, 2) \rangle] = \langle (2, 2) \rangle.$$

Hence,$\dfrac{\integer_4 \times \integer_6}{\langle (2, 2) \rangle}$ is not an integral domain.

Example. In the ring $\integer_2 \times \integer_{10}$ , consider the principal ideal $\langle (1, 5) \rangle$ .

(a) List the elements of $\langle (1, 5) \rangle$ .

(b) List the elements of the cosets of $\langle (1, 5) \rangle$ .

(c) Is the quotient ring $\dfrac{\integer_2 \times \integer_{10}}{\langle (1, 5) \rangle}$ a field?

(a) Note that the additive subgroup generated by $(1, 5)$ has only two elements. It's not the same as the ideal generated by $(1, 5)$ , so I can't find the elements of the ideal by taking additive multiples of $(1, 5)$ . I'll find the elements of the ideal $\langle (1, 5) \rangle$ by multiplying $(1, 5)$ by the elements of $\integer_2 \times \integer_{10}$ , then throwing out duplicates. The computation is routine, if a bit tedious.

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & element & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 3)$ & & $(0, 4)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot (1, 5)$ & & $(0, 0)$ & & $(0, 5)$ & & $(0, 0)$ & & $(0, 5)$ & & $(0, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & element & & $(0, 5)$ & & $(0, 6)$ & & $(0, 7)$ & & $(0, 8)$ & & $(0, 9)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot (1, 5)$ & & $(0, 5)$ & & $(0, 0)$ & & $(0, 5)$ & & $(0, 0)$ & & $(0, 5)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & element & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & & $(1, 3)$ & & $(1, 4)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot (1, 5)$ & & $(1, 0)$ & & $(1, 5)$ & & $(1, 0)$ & & $(1, 5)$ & & $(1, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & element & & $(1, 5)$ & & $(1, 6)$ & & $(1, 7)$ & & $(1, 8)$ & & $(1, 9)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot (1, 5)$ & & $(1, 5)$ & & $(1, 0)$ & & $(1, 5)$ & & $(1, 0)$ & & $(1, 5)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Removing duplicates, I have

$$\langle (1, 5) \rangle = \{(0, 0), (0, 5), (1, 0), (1, 5)\}.\quad\halmos$$

(b) Since the ideal has 4 elements and the ring has 20, there must be 5 cosets.

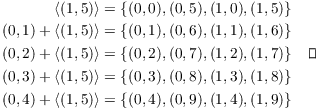
$$\eqalign{ \langle (1, 5) \rangle & = \{(0, 0), (0, 5), (1, 0), (1, 5)\} \cr (0, 1) + \langle (1, 5) \rangle & = \{(0, 1), (0, 6), (1, 1), (1, 6)\} \cr (0, 2) + \langle (1, 5) \rangle & = \{(0, 2), (0, 7), (1, 2), (1, 7)\} \cr (0, 3) + \langle (1, 5) \rangle & = \{(0, 3), (0, 8), (1, 3), (1, 8)\} \cr (0, 4) + \langle (1, 5) \rangle & = \{(0, 4), (0, 9), (1, 4), (1, 9)\} \cr}\quad\halmos$$

(c) Note that $(0, 1) + \langle (1, 5) \rangle$ is the identity.

$$[(0, 2) + \langle (1, 5) \rangle] [(0, 3) + \langle (1, 5) \rangle] = (0, 1) + \langle (1, 5) \rangle.$$

$$[(0, 4) + \langle (1, 5) \rangle] [(0, 4) + \langle (1, 5) \rangle] = (0, 1) + \langle (1, 5) \rangle.$$

Since every nonzero coset has a multiplicative inverse, the quotient ring is a field.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga