Ring Homomorphisms

Definition. Let R and S be rings. A ring homomorphism (or a ring map for short) is a function $f: R \rightarrow S$ such that:

(a) For all $x, y \in R$ , $f(x + y) = f(x) + f(y)$ .

(b) For all $x, y \in R$ , $f(x y) = f(x)f(y)$ .

Usually, we require that if R and S are rings with 1, then

(c) $f(1_R) = 1_S$ .

This is automatic in some cases; if there is any question, you should read carefully to find out what convention is being used.

The first two properties stipulate that f should "preserve" the ring structure --- addition and multiplication.

Example. ( A ring map on the integers mod 2) Show that the following function $f: \integer_2 \to \integer_2$ is a ring map:

$$f(x) = x^2.$$

First,

$$f(x + y) = (x + y)^2 = x^2 + 2 x y + y^2 = x^2 + y^2 = f(x) + f(y).$$

$2 x y = 0$ because 2 times anything is 0 in $\integer_2$ .

Next,

$$f(x y) = (x y)^2 = x^2 y^2 = f(x) f(y).$$

The second equality follows from the fact that $\integer_2$ is commutative.

Note also that $f(1) = 1^2 = 1$ .

Thus, f is a ring homomorphism.

Example. ( An additive function which is not a ring map) Show that the following function $g: \integer \to \integer$ is not a ring map:

$$g(x) = 2 x.$$

Note that

$$g(x + y) = 2(x + y) = 2 x + 2 y = g(x ) + g(y).$$

Therefore, g is additive --- that is, g is a homomorphism of abelian groups.

But

$$g(1 \cdot 3) = g(3) = 2 \cdot 3 = 6, \quad\hbox{while}\quad g(1) g(3) = (2 \cdot 1)(2 \cdot 3) = 12.$$

Thus, $g(1 \cdot 3) \ne g(1) g(3)$ , so g is not a ring map.

Lemma. Let R and S be rings and let $f: R \to S$ be a ring map.

(a) $f(0) = 0$ .

(b) $f(-r) = -f(r)$ for all $r \in R$ .

Proof. (a)

$$f(0) = f(0 + 0) = f(0) + f(0), \quad\hbox{so}\quad f(0) = 0.$$

(b) By (a),

$$0 = f(0) = f(r + (-r)) = f(r) + f(-r).$$

But this says that $f(-r)$ is the additive inverse of $f(r)$ , i.e. $f(-r) = -f(r)$ .

These properties are useful, and they also lend support to the idea that ring maps "preserve" the ring structure. Now I know that a ring map not only preserves addition and multiplication, but 0 and additive inverses as well.

Warning! A ring map f must satisfy $f(0) = 0$ and $f(-r) = -f(r)$ , but these are not part of the definition of a ring map. To check that something is a ring map, you check that it preserves sums and products.

On the other hand, if a function does not satisfy $f(0) = 0$ and $f(-r) = -f(r)$ , then it isn't a ring map.

Example. ( Showing that a function is not a ring map) (a) Show that the following function $f: \integer \to \integer$ is not a ring map:

$$f(x) = 2 x + 5.$$

(b) Show that the following $g: \integer \to \integer$ is not a ring map:

$$g(x) = 3 x.$$

(a) $f(0) = 5 \ne 0$ .

(b) $g(0) = 0$ and $g(-n) = -g(n)$ for all $n \in \integer$ . Nevertheless, g is not a ring map:

$$g(3 \cdot 2) = g(6) = 3 \cdot 6 = 18, \quad\hbox{but}\quad g(3) \cdot g(2) = (3 \cdot 3) \cdot (3 \cdot 2) = 54.$$

Thus, $g(3 \cdot 2) \ne g(3) \cdot g(2)$ , so g does not preserve products.

Lemma. Let R, S, and T be rings, and let $f: R \to S$ and $g: S \to T$ be ring maps. Then the composite $g \cdot f: R \to T$ is a ring map.

Proof. Let $x, y \in R$ . Then

$$(g \cdot f)(x + y) = g(f(x + y)) = g(f(x) + f(y)) = g(f(x)) + g(f(y)) = (g \cdot f)(x) + (g \cdot f)(y).$$

$$(g \cdot f)(x \cdot y) = g(f(x \cdot y)) = g(f(x) \cdot f(y)) = g(f(x)) \cdot g(f(y)) = (g \cdot f)(x) \cdot (g \cdot f)(y).$$

If, in addition, R, S, and T are rings with identity, then

$$(g \cdot f)(1) = g(f(1)) = g(1) = 1.$$

Therefore, $g \cdot f$ is a ring map.

There is an important relationship between ring maps and ideals. I'll consider half of the relationship now.

Definition. The kernel of a ring map $\phi: R \to S$ is

$$\ker \phi = \{r \in R \mid \phi(r) = 0\}.$$

The image of a ring map $\phi: R \rightarrow S$ is

$$\im \phi = \{\phi(r) \mid r \in R\}.$$

The kernel of a ring map is like the null space of a linear transformation of vector spaces. The image of a ring map is like the column space of a linear transformation.

Proposition. The kernel of a ring map is a two-sided ideal.

In fact, I'll show later that every two-sided ideal arises as the kernel of a ring map.

Proof. Let $\phi: R \rightarrow S$ be a ring map. Let $x, y \in \ker \phi$ , so $\phi(x) = 0$ and $\phi(y) = 0$ . Then

$$\phi(x + y) = \phi(x) + \phi(y) = 0 + 0 = 0.$$

Hence, $x + y \in \ker \phi$ .

Since $\phi(0) = 0$ , $0 \in \ker \phi$ .

Next, if $x \in \ker \phi$ , then $\phi(x) = 0$ . Hence, $-\phi(x) = 0$ , so $\phi(-x) = 0$ (why?), so $-x \in \ker \phi$ .

Finally, let $x \in \ker \phi$ and let $r \in R$ .

$$\phi(r x) = \phi(r) \phi(x) = \phi(r) \cdot 0 = 0,$$

$$\phi(x r) = \phi(x) \phi(r) = 0 \cdot \phi(r) = 0.$$

It follows that $r x, x r \in \ker \phi$ . Hence, $\ker \phi$ is a two-sided ideal.

I'll omit the proof of the following result. Note that it says the image of a ring map is a subring, not an ideal.

Proposition. Let $\phi: R \rightarrow S$ be a ring map. Then $\im \phi$ is a subring of S.

Definition. Let R and S be rings. A ring isomorphism from R to S is a bijective ring homomorphism $f: R \to S$ .

If there is a ring isomorphism $f: R \to S$ , R and S are isomorphic. In this case, we write $R \approx S$ .

Heuristically, two rings are isomorphic if they are "the same" as rings.

An obvious example: If R is a ring, the identity map $\hbox{id}: R \rightarrow R$ is an isomorphism of R with itself.

Since a ring isomorphism is a bijection, isomorphic rings must have the same cardinality. So, for example, $\integer_6 \not\approx \integer_{42}$ , because the two rings have different numbers of elements.

However, $\integer$ and $\rational$ have the "same number" of elements --- the same cardinality --- but they are not isomorphic as rings. (Quick reason: $\rational$ is a field, while $\integer$ is only an integral domain.)

I've been using this construction informally in some examples. Here's the precise definition.

Definition. Let R and S be rings. The product ring $R \times S$ of R and S is the set consisting of all ordered pairs $(r, s)$ , where $r \in R$ and $s \in S$ . Addition and multiplication are defined component-wise: For $a, b \in R$ and $x, y \in S$ ,

$$(a, x) + (b, y) = (a + b, x + y).$$

$$(a, x) \cdot (b, y) = (a \cdot b, x \cdot y).$$

I won't go through the verification of all the axioms; basically, everything works because everything works in each component separately. For example, here's the verification of the associative law for addition. Let $a, b, c \in R$ , $x, y, z \in S$ . Then

$$[(a, x) + (b, y)] + (c, z) = (a + b, x + y) + (c, z) = ((a + b) + c, (x + y) + z) = (a + (b + c), x + (y + z)) =$$

$$(a, x) + (b + c, y + z) = (a, x) + [(b, y) + (c, z)].$$

The third equality used associativity of addition in R and in S.

The additive identity is $(0, 0)$ ; the additive inverse $-(r, s)$ of $(r, s)$ is $(-r, -s)$ . And so on. Try out one or two of the other axioms for yourself just to get a feel for how things work.

Example. ( A ring isomorphic to a product of rings) Show that $\integer_6 \approx \integer_2 \times \integer_3$ .

$\integer_6 \approx \{0, 1, 2, 3, 4, 5\}$ with addition and multiplication mod 6. On the other hand,

$$\integer_2 \times \integer_3 = \{(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2)\}.$$

One ring consists of single elements, while the other consists of pairs. Nevertheless, these rings are isomorphic --- they are the same as rings.

Here are the addition and multiplication tables for $\integer_6$ :

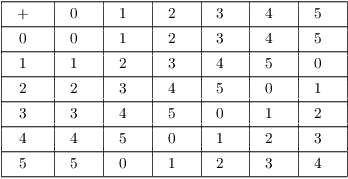
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 3 & & 4 & & 5 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 3 & & 4 & & 5 & & 0 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 4 & & 5 & & 0 & & 1 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 4 & & 5 & & 0 & & 1 & & 2 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 5 & & 0 & & 1 & & 2 & & 3 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

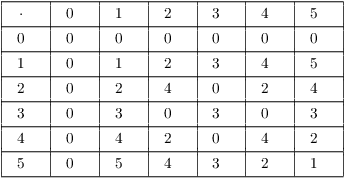
$$ \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & & 0 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 0 & & 2 & & 4 & & 0 & & 2 & & 4 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 0 & & 3 & & 0 & & 3 & & 0 & & 3 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 0 & & 4 & & 2 & & 0 & & 4 & & 2 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 0 & & 5 & & 4 & & 3 & & 2 & & 1 & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here are the addition and multiplication tables for $\integer_2 \times \integer_3$ .

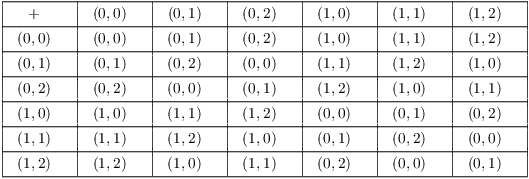
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 1)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 0)$ & & $(1, 1)$ & & $(1, 2)$ & & $(1, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 2)$ & & $(0, 2)$ & & $(0, 0)$ & & $(0, 1)$ & & $(1, 2)$ & & $(1, 0)$ & & $(1, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 1)$ & & $(1, 1)$ & & $(1, 2)$ & & $(1, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 2)$ & & $(1, 2)$ & & $(1, 0)$ & & $(1, 1)$ & & $(0, 2)$ & & $(0, 0)$ & & $(0, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

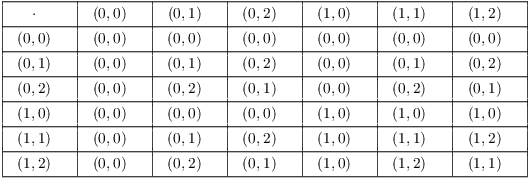
$$ \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 1)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 2)$ & & $(0, 0)$ & & $(0, 2)$ & & $(0, 1)$ & & $(0, 0)$ & & $(0, 2)$ & & $(0, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(0, 0)$ & & $(1, 0)$ & & $(1, 0)$ & & $(1, 0)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 1)$ & & $(0, 0)$ & & $(0, 1)$ & & $(0, 2)$ & & $(1, 0)$ & & $(1, 1)$ & & $(1, 2)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 2)$ & & $(0, 0)$ & & $(0, 2)$ & & $(0, 1)$ & & $(1, 0)$ & & $(1, 2)$ & & $(1, 1)$ & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The two rings each have 6 elements, so it's easy to define a bijection from one to the other --- for example,

$$f(0) = (0, 0), f(1) = (0, 1), f(2) = (0, 2), f(3) = (1, 0), f(4) = (1, 1), f(5) = (1, 2).$$

However, this is not a ring isomorphism:

$$f(1 + 2) = f(3) = (1, 0), \quad\hbox{while}\quad f(1) + f(2) = (0, 1) + (0, 2) = (0, 0).$$

Thus, $f(1 + 2) \ne f(1) + f(2)$ .

It turns out, however, that the following map gives a ring isomorphism $\integer_6 \to \integer_2 \times \integer_3$ :

$$f(0) = (0, 0), f(1) = (1, 1), f(2) = (0, 2), f(3) = (1, 0), f(4) = (0, 1), f(5) = (1, 2).$$

It's obvious that the map is a bijection. To prove that this is a ring isomorphism, you'd have to check 36 cases for $f(r + s) = f(r) + f(s)$ and another 36 cases for $f(r\cdot s) = f(r)\cdot f(s)$ .

Example. ( Showing that a product of rings which is not isomorphic to another ring) Show that the rings $\integer_4$ and $\integer_2 \times \integer_2$ are not isomorphic.

$\integer_4$ and $\integer_2 \times \integer_2$ aren't isomorphic as groups under addition. Since a ring isomorphism must give an isomorphism of the two rings considered as groups under addition, $\integer_4$ and $\integer_2 \times \integer_2$ can't be isomorphic as rings.

To see this directly, suppose $f: \integer_4 \to \integer_2 \times \integer_2$ is an isomorphism. Then $f(1) + f(1) = (0, 0)$ , because everything in $\integer_2 \times \integer_2$ gives 0 when added to itself. But since f is a ring map,

$$f(1) + f(1) = f(1 + 1) = f(2).$$

Therefore, $f(2) = (0, 0)$ .

But I know that $f(0) = (0, 0)$ , because any ring map takes the additive identity to the additive identity. Now I have two elements 2 and 0 which both map to $(0, 0)$ , and this contradicts the fact that f is injective.

Therefore, there is no such f, and the rings aren't isomorphic.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga