The Group of Units in the Integers mod n

The group $\integer_n$ consists of the elements $\{0, 1, 2, \ldots, n - 1\}$ with addition mod n as the operation. You can also multiply elements of $\integer_n$ , but you do not obtain a group: The element 0 does not have a multiplicative inverse, for instance.

However, if you confine your attention to the units in $\integer_n$ --- the elements which have multiplicative inverses --- you do get a group under multiplication mod n. It is denoted $U_n$ , and is called the group of units in $\integer_n$ .

Proposition. Let $U_n$ be the set of units in $\integer_n$ , $n \ge 1$ . Then $U_n$ is a group under multiplication mod n.

Proof. To show that multiplication mod n is a binary operation on $U_n$ , I must show that the product of units is a unit.

Suppose $a, b \in U_n$ . Then a has a multiplicative inverse $a^{-1}$ and b has a multiplicative inverse $b^{-1}$ . Now

$$(b^{-1} a^{-1})(a b) = b^{-1} (a^{-1} a) b = b^{-1} (1) b = b^{-1} b = 1,$$

$$(a b) (b^{-1 } a^{-1}) = a (b b^{-1}) a^{-1} = a (1) a^{-1} = a a^{-1} = 1.$$

Hence, $b^{-1} a^{-1}$ is the multiplicative inverse of $a b$ , and $a b$ is a unit. Therefore, multiplication mod n is a binary operation on $U_n$ .

(By the way, you may have seen the result $(a b)^{-1} = b^{-1} a^{-1}$ when you studied linear algebra; it's a standard identity for invertible matrices.)

I'll take it for granted that multiplication mod n is associative.

The identity element for multiplication mod n is 1, and 1 is a unit in $\integer_n$ (with multiplicative inverrse 1).

Finally, every element of $U_n$ has a multiplicative inverse, by definition.

Therefore, $U_n$ is a group under multiplication mod n.

Before I give some examples, recall that m is a unit in $\integer_n$ if and only if m is relatively prime to n.

Example. ( The groups of units in $\integer_{14}$ ) Construct a multiplication table for $U_{14}$ .

$U_{14}$ consists of the elements of $\integer_{14}$ which are relatively prime to 14. Thus,

$$U_{14} = \{1, 3, 5, 9, 11, 13\}.$$

You multiply elements of $U_{14}$ by multiplying as if they were integers, then reducing mod 14. For example,

$$11 \cdot 13 = 143 = 3 \mod{14}, \quad\hbox{so}\quad 11 \cdot 13 = 3 \quad\hbox{in}\quad \integer_{14}.$$

Here's the multiplication table for $U_{14}$ :

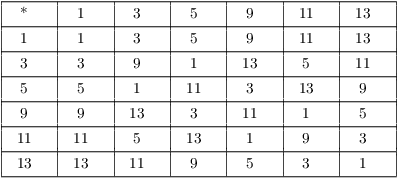
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & * & & 1 & & 3 & & 5 & & 9 & & 11 & & 13 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 3 & & 5 & & 9 & & 11 & & 13 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 9 & & 1 & & 13 & & 5 & & 11 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 5 & & 1 & & 11 & & 3 & & 13 & & 9 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 9 & & 9 & & 13 & & 3 & & 11 & & 1 & & 5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 11 & & 11 & & 5 & & 13 & & 1 & & 9 & & 3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 13 & & 13 & & 11 & & 9 & & 5 & & 3 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Notice that the table is symmetric about the main diagonal. Multiplication mod 14 is commutative, and $U_{14}$ is an abelian group.

Be sure to keep the operations straight: The operation in $\integer_{14}$ is addition mod 14, while the operation in $U_{14}$ is multiplication mod 14.

Example. ( The groups of units in $\integer_p$ ) What are the elements of $U_p$ if p is a prime number?

Construct a multiplication table for $U_{11}$ .

If p is prime, then all the positive integers smaller than p are relatively prime to p. Thus,

$$U_p = \{1, 2, 3, \ldots, p - 1\}.$$

For example, in $\integer_{11}$ , the group of units is

$$U_{11} = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}.$$

The operation in $U_{11}$ is multiplication mod 11. For example, $8\cdot 6 = 4$ in $U_{11}$ . Here's the multiplication table for $U_{11}$ :

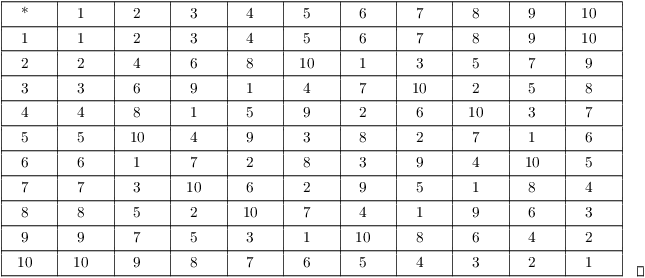
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & * & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & & 9 & & 10 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & & 9 & & 10 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 2 & & 4 & & 6 & & 8 & & 10 & & 1 & & 3 & & 5 & & 7 & & 9 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 3 & & 6 & & 9 & & 1 & & 4 & & 7 & & 10 & & 2 & & 5 & & 8 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 4 & & 4 & & 8 & & 1 & & 5 & & 9 & & 2 & & 6 & & 10 & & 3 & & 7 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 5 & & 5 & & 10 & & 4 & & 9 & & 3 & & 8 & & 2 & & 7 & & 1 & & 6 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 6 & & 6 & & 1 & & 7 & & 2 & & 8 & & 3 & & 9 & & 4 & & 10 & & 5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 7 & & 7 & & 3 & & 10 & & 6 & & 2 & & 9 & & 5 & & 1 & & 8 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 8 & & 8 & & 5 & & 2 & & 10 & & 7 & & 4 & & 1 & & 9 & & 6 & & 3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 9 & & 9 & & 7 & & 5 & & 3 & & 1 & & 10 & & 8 & & 6 & & 4 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 10 & & 10 & & 9 & & 8 & & 7 & & 6 & & 5 & & 4 & & 3 & & 2 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

Example. ( The subgroup generated by an element) List the elements of $\langle 7 \rangle$ in $U_{18}$ .

The elements in $\{0, 1, 2, \ldots, 17\}$ which are relatively prime to 18 are the elements of $U_{18}$ :

$$U_{18} = \{1, 5, 7, 11, 13, 17\}.$$

The operation is multiplication mod 18.

Since the operation is multiplication, the cyclic subgroup generated by 7 consists of all powers of 7:

$$7^0 = 1, \quad 7^1 = 7, \quad 7^2 = 13.$$

I can stop here, because $7^3 = 343 = 1$ mod 18. So

$$\langle 7 \rangle = \{1, 7, 13\}.\quad\halmos$$

For the next result, I'll need a special case of Lagrange's theorem: The order of an element in a finite group divides the order of the group. I'll prove Lagrange's theorem when I discuss cosets.

As an example, in a group of order 10, an element may have order 1, 2, 5, or 10, but it may not have order 8.

Theorem. ( Fermat's Theorem) If a and p are integers, p is prime, and $p \notdiv a$ , then

$$a^{p-1} = 1 \mod{p}.$$

Proof. If p is prime, then

$$U_p = \{1, 2, 3, \ldots, p - 1\}.$$

In particular, $|U_p| = p - 1$ .

Now if $p \notdiv a$ , then

$$a = b \mod{p}, \quad\hbox{where}\quad b \in \{1, 2, 3, \ldots, p - 1\}.$$

Lagrange's theorem implies that the order of an element divides the order of the group. As a result, $b^{p-1} = 1$ in $U_p$ . Hence,

$$a^{p-1} = b^{p-1} = 1 \mod{p}.\quad\halmos$$

Example. ( Using Fermat's Theorem to reduce a power) Compute $77^{2401} \mod{97}$ .

The idea is to use Fermat's theorem to reduce the power to smaller numbers where you can do the computations directly.

97 is prime, and $97 \notdiv 77$ . By Fermat's theorem,

$$77^{96} = 1 \mod{97}.$$

So

$$77^{2401} = 77^{2400}\cdot 77 = (77^{96})^{25}\cdot 77 = 1 \cdot 77 = 77 \mod{97}.\quad\halmos$$

Example. 157 is prime. Reduce $138^{155} \mod{157}$ to a number in $\{0, 1, \ldots 156\}$ .

By Fermat's Theorem, $138^{156} = 1 \mod{157}$ . So

$$\eqalign{ x & = 138^{155} \mod{157} \cr 138 x & = 138^{156} = 1 \mod{157} \cr}$$

Next,

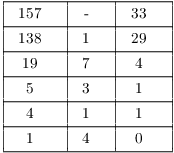
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 157 & & - & & 33 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 138 & & 1 & & 29 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 19 & & 7 & & 4 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 5 & & 3 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 4 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 1 & & 4 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\eqalign{ (-29) \cdot 157 + 33 \cdot 138 & = 1 \cr 33 \cdot 138 & = 1 \mod{157} \cr}$$

Hence, $138^{-1} = 33 \mod{157}$ .

So

$$\eqalign{ 33 \cdot 138 x & = 33 \cdot 1 \mod{157} \cr x & = 33 \mod{157} \cr} \quad\halmos$$

Here is a result which is related to Fermat's Theorem.

Theorem. ( Wilson's Theorem) p is prime if and only if

$$(p - 1)! = -1 \mod{p}.$$

Proof. If p is prime, consider the numbers in $\{1, 2, \ldots p - 1\}$ . Note that if $x = x^{-1} \mod{p}$ , then $x \cdot x = 1 \mod{p}$ , so

$$\eqalign{ x^2 - 1 & = 0 \mod{p} \cr (x - 1)(x + 1) & = 0 \mod{p} \cr}$$

Hence, $p \mid (x - 1)(x + 1)$ , and by Euclid's lemma either $p \mid x - 1$ and $x = 1 \mod{p}$ or $p \mid x + 1$ and $x = -1 = p - 1 \mod{p}$ .

In other words, the only two numbers in $\{1, 2, \ldots p - 1\}$ which are their own multiplicative inverses are 1 and $p - 1$ . The other numbers in this set pair up as a and $a^{-1}$ with $a \ne a^{-1} \mod{p}$ . Hence, the product simplifies to

$$1 \cdot (\hbox{pairs whose product is 1}) \cdot (-1) = -1 \mod{p}.$$

On the other hand, if p is not prime, then p is composite. If $p = a b$ where $1 < a < b < p$ , then

$$(p - 1)! = 1 \cdots a \cdots b \cdot (p - 1) = 0 \mod{p}.$$

Thus, $(p - 1)! \ne -1 \mod{p}$ .

The only other possibility is that $p = q^2$ , where q is a prime.

If $q > 2$ , then

$$p = q^2 > 2 q > q.$$

Then both $2 q$ and q appear in the set $\{1, 2, \ldots p - 1\}$ , so the product $1 \cdot 2 \cdots (p - 1)$ contains a factor of $2 q \cdot q = 2 p = 0 mod{p}$ . Once again, $(p - 1)! = 0 \ne -1 \mod{p}$ .

The final case is $q = 2$ and $p = q^2 = 4$ . Then

$$(p - 1)! = 1 \cdot 2 \cdot 3 = 6 = 2 \ne 0 \mod{4}.\quad\halmos$$

Example. 131 is prime. Reduce $\dfrac{130!}{33} \mod{131}$ to a number in $\{0, 1, \ldots 130\}$ .

By Wilson's Theorem, $130! = -1 \mod{131}$ . So

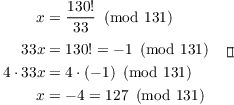
$$\eqalign{ x & = \dfrac{130!}{33} \mod{131} \cr \noalign{\vskip2pt} 33 x & = 130! = -1 \mod{131} \cr 4 \cdot 33 x & = 4 \cdot (-1) \mod{131} \cr x & = -4 = 127 \mod{131} \cr} \quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga