Antiderivatives

$F(x)$ is an antiderivative of $f(x)$ if

$$\der {F(x)} x = f(x).$$

Notation:

$$\int f(x)\,dx = F(x) + C.$$

For example,

$$\int x^3\,dx = \dfrac{1}{4} x^4 + C, \quad\hbox{because}\quad \der {} x \left(\dfrac{1}{4} x^4\right) = x^3.$$

In fact, all of the following functions are antiderivatives of $x^3$ , because they all differentiate to $x^3$ :

$$\dfrac{1}{4} x^4, \quad \dfrac{1}{4} x^4 + 1, \quad \dfrac{1}{4} x^4 - 13, \quad \dfrac{1}{4} x^4 + 157.$$

This is the reason for the "$+ C$ " in the notation: You can add any constant to the "basic" antiderivative $\dfrac{1}{4} x^4$ and come up with another antiderivative.

C is called the arbitrary constant.

Remark. (a) Antiderivatives are often referred to as indefinite integrals, and sometimes I'll refer to $\displaystyle \int f(x)\,dx$ as "the integral of $f(x)$ with respect to x". This terminology is actually a bit misleading, but it's traditional, so I'll often use it. There is another kind of "integral" --- the definite integral --- which is probably more deserving of the name.

(b) The notation "$\displaystyle \int f(x)\,dx$ " will also be used for definite integrals. The integral sign $\displaystyle \int$ is a stretched-out "S", and comes from the fact that definite integrals are defined in terms of sums.

"$\displaystyle \int (\hphantom{x})\,dx$ " is a mathematical object called an operator, which roughly speaking is a function which takes functions as inputs and produces functions as outputs. Despite appearances, "$dx$ " isn't a separate thing; in fact, "$\displaystyle \int (\hphantom{x})\,dx$ " is the whole name of the antidervative operator. It's a weird name --- it consists of three symbols ("$\displaystyle \int$ ", "d", and "x"), and has a space between the "$\displaystyle \int$ " and the "$dx$ " for the input function.

I'll come back to this again when I discuss substitution, since at that point this can become a source of confusion.

Every differentiation formula has a corresponding antidifferentiation formula. This makes it easy to derive antidifferentiation rules from the rules for differentiation.

Theorem. ( Power Rule) For $n \ne -1$ ,

$$\int x^n\,dx = \dfrac{1}{n + 1} x^{n+1} + C.$$

Proof. This follows from the fact that

$$\der {} x \dfrac{1}{n + 1} x^{n+1} = x^n.$$

(Notice that the expression on the left is undefined if $n = -1$ .)

Example. Compute the following antiderivatives:

(a) $\displaystyle \int x^{100}\,dx$ .

(b) $\displaystyle \int \sqrt{x}\,dx$ .

(c) $\displaystyle \int \dfrac{1}{x^5}\,dx$ .

(d) $\displaystyle \int \dfrac{1}{x^{5/3}}\,dx$ .

(a)

$$\int x^{100}\,dx = \dfrac{1}{101} x^{101} + C.$$

(b)

$$\int \sqrt{x}\,dx = \int x^{1/2}\,dx = \dfrac{2}{3} x^{3/2} + C.$$

(c)

$$\int \dfrac{1}{x^5}\,dx = \int x^{-5}\,dx = -\dfrac{1}{4} x^{-4} + C.$$

(d)

$$\int \dfrac{1}{x^{5/3}}\,dx = \int x^{-5/3}\,dx = -\dfrac{3}{2} x^{-2/3} + C.\quad\halmos$$

Theorem.

$$\int \left(f(x) + g(x)\right)\,dx = \int f(x)\,dx + \int g(x)\,dx.$$

$$\int k \cdot f(x)\,dx = k \int f(x)\,dx, \quad\hbox{if k is a constant}.$$

$$\int k\,dx = kx + \int f(x)\,dx, \quad\hbox{if k is a constant}.$$

Proof. I'll prove the first formula by way of example; see if you can prove the others.

Suppose that

$$\der {} x F(x) = f(x) \quad\hbox{and}\quad \der {} x G(x) = g(x).$$

By definition, this means that

$$\int f(x)\,dx = F(x) + C \quad\hbox{and}\quad \int g(x)\,dx = G(x) + C.$$

By the rule for the derivative of a sum,

$$\der {} x (F(x) + G(x)) = \der {} x F(x) + \der {} x G(x) = f(x) + g(x).$$

By definition, this means that

$$\int (f(x) + g(x))\,dx = F(x) + G(x) + C.\quad\halmos$$

Example. Compute the following antiderivatives:

(a) $\displaystyle \int 8 x^{10}\,dx$ .

(b) $\displaystyle \int \left(3 x^4 + 2 x + 5\right)\,dx$ .

(a)

$$\int 8 x^{10}\,dx = 8 \int x^{10}\,dx = \dfrac{8}{11} x^{11} + C.$$

(b)

$$\int \left(3 x^4 + 2 x + 5\right)\,dx = 3 \int x^4\,dx + 2 \int x\,dx + 5 \int\,dx = \dfrac{3}{5} x^5 + x^2 + 5 x + C.\quad\halmos$$

Since the derivative of a product is not the product of the derivatives, you can't expect that it would work that way for antiderivatives, either.

Example. Compute $\displaystyle \int (x^2 - 1)(x^4 + 2)\,dx$ .

To do this antiderivative, I don't antidifferentiate $x^2 - 1$ and $x^4 + 2$ separately. Instead, I multiply out, then use the rules I discussed above.

$$\int (x^2 - 1)(x^4 + 2)\,dx = \int \left(x^6 - x^4 + 2 x^2 - 2\right)\,dx = \dfrac{1}{7} x^7 - \dfrac{1}{5} x^5 + \dfrac{2}{3} x^3 - 2 x + C.\quad\halmos$$

Likewise, the derivative of a quotient is not the quotient of the derivatives, and it doesn't work that way for antiderivatives.

Example. Compute $\displaystyle \int \dfrac{x^4 + 1}{x^2}\,dx$ .

Don't antidifferentiate $x^4 + 1$ and $x^2$ separately! Instead, divide the bottom into the top:

$$\int \dfrac{x^4 + 1}{x^2}\,dx = \int \left(x^2 + x^{-2}\right)\,dx = \dfrac{1}{3} x^3 - x^{-1} + C.\quad\halmos$$

Every differentiation rule gives an antidifferentiation rule. So

$$\der {} x \sin x = \cos x \quad\hbox{means that}\quad \int \cos x\,dx = \sin x + C.$$

Example. Compute $\displaystyle \int \left(5 x^7 + 4 \cos x\right)\,dx$ .

For example,

$$\int \left(5 x^7 + 4 \cos x\right)\,dx = \dfrac{5}{8} x^8 + 4 \sin x + C.\quad\halmos$$

Example. $\der y x = \left(x^2 + \dfrac{1}{x^2}\right)^2$ and $y(1) = \dfrac{1}{5}$ . Find y.

To find y, antidifferentiate $\der y x$ :

$$y = \int \der y x\,dx = \int \left(x^2 + \dfrac{1}{x^2}\right)^2\,dx = \int \left(x^4 + 2 + \dfrac{1}{x^4}\right)\,dx = \dfrac{1}{5} x^5 + 2 x - \dfrac{2}{3}\dfrac{1}{x^3} + C.$$

$y(1) = \dfrac{1}{5}$ :

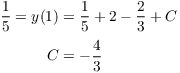
$$\eqalign{ \dfrac{1}{5} = y(1) & = \dfrac{1}{5} + 2 - \dfrac{2}{3} + C \cr \noalign{\vskip2pt} C & = -\dfrac{4}{3} \cr}$$

Therefore,

$$y = \dfrac{1}{5} x^5 + 2 x - \dfrac{2}{3}\dfrac{1}{x^3} - \dfrac{4}{3}.$$

This process is a simple example of solving a differential equation with an initial condition.

Example. Suppose an object moves with constant acceleration a. Its initial velocity is $v_0$ , and its initial position is $s_0$ . Find its position function $s(t)$ .

First, $a(t) = v'(t) = \der v t$ , so

$$v = \int a(t)\,dt = \int a\,dt = a t + C.$$

When $t = 0$ , $v = v_0$ , so

$$v_0 = a\cdot 0 + C, \quad C = v_0.$$

Therefore,

$$v = a t + v_0.$$

Next, $v(t) = s'(t) = \der s t$ , so

$$s = \int v(t)\,dt = \int \left(a t + v_0\right)\,dt = \dfrac{1}{2} a t^2 + v_0 t + D.$$

When $t = 0$ , $s = s_0$ :

$$s_0 = \dfrac{1}{2} a \cdot 0 + v_0\cdot 0 + D, \quad D = s_0.$$

Therefore,

$$s = \dfrac{1}{2} a t^2 + v_0 t + s_0.$$

For example, an object falling near the surface of the earth experiences a constant acceleration of -32 feet per second per second (negative, since the object's height s is decreasing). Its height at time t is

$$s = -16 t^2 + v_0 t + s_0.$$

Here $v_0$ is its initial velocity and $s_0$ is the height from which it's dropped.

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga