The Chain Rule

The Chain Rule computes the derivative of the composite of two functions. The composite $(f\circ g)(x)$ is just "g inside f" --- that is,

$$(f \circ g)(x) = f\left(g(x)\right).$$

(Note that this is not multiplication!)

Here are some examples:

$$(x^3 + x^2 - 7x + 1)^{99} \quad\hbox{is}\quad g(x) = x^3 + x^2 - 7x + 1 \quad\hbox{inside}\quad f(x) = x^{99}.$$

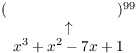
$$\matrix{ (\hphantom{x^3 + x^2 - 7x + 1})^{99} \cr \uparrow \cr x^3 + x^2 - 7x + 1 \cr}$$

$$\dfrac{1}{x^2 - x - 1} \quad\hbox{is}\quad g(x) = x^2 - x - 1 \quad\hbox{inside}\quad f(x) = \dfrac{1}{x}.$$

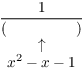
$$\matrix{ \dfrac{1}{(\hphantom{x^2 - x - 1})} \cr \uparrow \cr x^2 - x - 1 \cr}$$

$$\sin (x^2) \quad\hbox{is}\quad g(x) = x^2 \quad\hbox{inside}\quad f(x) = \sin x.$$

$$\matrix{\sin & (\hphantom{x^2}) \cr & \uparrow \cr & x^2 \cr}$$

Here's a more complicated example:

$$\cos \dfrac{1}{x^2 - 2x + 5} \quad\hbox{is}\quad h(x) = x^2 - 2x + 5 \quad\hbox{inside}\quad g(x) = \dfrac{1}{x} \quad\hbox{inside}\quad f(x) = \cos x.$$

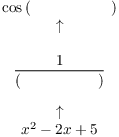
$$\matrix{ \cos \left(\hphantom{\dfrac{1}{x^2 - 2x + 5}}\right) \cr \uparrow \cr \noalign{\smallskip} \cr \dfrac{1}{(\hphantom{x^2 - 2x + 5})} \cr \noalign{\smallskip} \cr \uparrow \cr x^2 - 2x + 5 \cr}$$

One way to tell which function is "inside" and which is "outside" is to think about how you would plug numbers in. For example, take $p(x) = \sin (x^2)$ . What would you do to compute $p(1.7)$ on your calculator? First, you'd square 1.7 --- $1.7^2 = 1.89$ . Next, you'd take the sine of that --- $\sin 1.89 \approx 0.94949$ .

The function you did first --- squaring --- is the inner function. The function you did second --- sine --- is the outer function.

Example. Suppose

$$f(x) = \dfrac{1}{x} \quad\hbox{and}\quad g(x) = x^2 + 1.$$

Compute $(f \circ g)(x)$ , $(g \circ f)(x)$ , and $(f \circ f)(x)$ .

$$(f \circ g)(x) = f\left(g(x)\right) = f\left(x^2 + 1\right) = \dfrac{1}{x^2 + 1}.$$

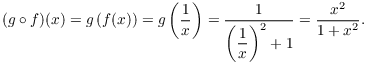
$$(g \circ f)(x) = g\left(f(x)\right) = g\left(\dfrac{1}{x}\right) = \dfrac{1}{\left(\dfrac{1}{x}\right)^2 + 1} = \dfrac{x^2}{1 + x^2}.$$

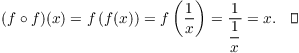
$$(f \circ f)(x) = f\left(f(x)\right) = f\left(\dfrac{1}{x}\right) = \dfrac{1}{\dfrac{1}{x}} = x.\quad\halmos$$

Theorem. ( Chain Rule) If f is differentiable at a and g is differentiable at $f(a)$ , then the composite function $(g \circ f)(x) = g(f(x))$ is differentiable at a, and its derivative is

$$(g \circ f)'(a) = g'\left(f(a)\right) f'(a).$$

In functional form, this is

$$\der {} x (g \circ f)(x) = \der {} x g\left(f(x)\right) = g'\left(f(x)\right) f'(x).$$

In words, you differentiate the outer function while holding the inner function fixed, then you differentiate the inner function.

The proof is pretty technical, and you can omit it if you're taking a typical first-term calculus course. It is given at the end. In the examples, I'll focus on how you use the Chain Rule to compute derivatives.

Example. Compute $\displaystyle \der {} x (x^3 + x^2 - 7x + 1)^{99}$ .

$(x^3 + x^2 - 7x + 1)^{99}$ looks like this:

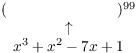
$$\matrix{ (\hphantom{x^3 + x^2 - 7x + 1})^{99} \cr \uparrow \cr x^3 + x^2 - 7x + 1 \cr}$$

Differentiate the outer function $(\hbox{junk})^{99}$ , obtaining $99(\hbox{junk})^{98}$ . What is "junk"? It's $x^3 + x^2 - 7x + 1$ . The first term in the Chain Rule is $99(x^3 + x^2 - 7x + 1)^{98}$ . (Notice that I differentiated the outer function, temporarily leaving the inner one untouched.)

Next, differentiate the inner function. The derivative of $x^3 + x^2 - 7x + 1$ is $3x^2 + 2x - 7$ .

Therefore,

$$\der {} x (x^3 + x^2 - 7x + 1)^{99} = 99 (x^3 + x^2 - 7x + 1)^{98} \cdot (3x^2 + 2x - 7).\quad\halmos$$

Example. Compute $\displaystyle \der {} x \left(\dfrac{1}{x^2 - x - 1}\right)$ .

While it would be correct to use the Quotient Rule, it's unnecessary.

$$\matrix{ \der {} x \left(\dfrac{1}{x^2 - x - 1}\right) & = & -\dfrac{1}{(x^2 - x - 1)^2} & \cdot & (2x - 1) \cr & & \uparrow & & \uparrow \cr & & \hbox{the derivative of} & & \hbox{the derivative of} \cr \noalign{\vskip2pt} & & \dfrac{1}{\hbox{junk}} & & x^2 - x - 1 \cr}$$

That is,

$$\der {} x \left(\dfrac{1}{x^2 - x - 1}\right) = \left(-\dfrac{1}{(x^2 - x - 1)^2}\right)(2 x - 1).$$

In general, you do not need to use the Quotient Rule to differentiate things of the form

$$\dfrac{\hbox{number}}{\hbox{junk}} \quad\hbox{or}\quad \dfrac{\hbox{junk}}{\hbox{number}}.$$

In the first case, use the Chain Rule as above. In the second case, divide the top by the number on the bottom.

Example. Compute $\displaystyle \der {} x \dfrac{1}{x + 5 x^3}$ .

$$\der {} x \dfrac{1}{x + 5 x^3} = \der {} x (x + 5 x^3)^{-1} = -(x + 5 x^3)^{-2}\cdot (1 + 15 x^2).\quad\halmos$$

In some of the examples which follow, I'll use the derivative formulas for $\sin x$ and $\cos x$ . They are:

$$\der {} x \sin x = \cos x \quad\hbox{and}\quad \der {} x \cos x = -\sin x.$$

Example. Compute $\displaystyle \der {} x \sin (x^2)$ .

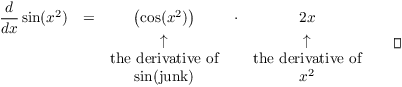
$$\matrix{ \der {} x \sin (x^2) & = & \left(\cos (x^2)\right) & \cdot & 2x \cr & & \uparrow & & \uparrow \cr & & \hbox{the derivative of} & & \hbox{the derivative of} \cr & & \sin (\hbox{junk}) & & x^2 \cr}\qquad \halmos$$

Example. Compute $\displaystyle \der {} x \cos \dfrac{1}{x^2 - 2 x + 5}$ .

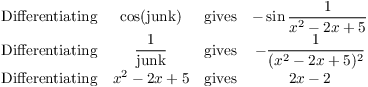
$$\matrix{ \hbox{Differentiating} & \cos (\hbox{junk}) & \hbox{gives} & -\sin \dfrac{1}{x^2 - 2x + 5} \cr \hbox{Differentiating} & \dfrac{1}{\hbox{junk}} & \hbox{gives} & -\dfrac{1}{(x^2 - 2x + 5)^2} \cr \hbox{Differentiating} & x^2 - 2x + 5 & \hbox{gives} & 2x - 2 \cr}$$

Therefore,

$$\der {} x \cos \dfrac{1}{x^2 - 2x + 5} = \left(-\sin \dfrac{1}{x^2 - 2x + 5}\right) \left(-\dfrac{1}{(x^2 - 2x + 5)^2}\right) \left(2x - 2\right).\quad\halmos$$

Example. f and g are differentiable functions. A table of some values for these functions is shown below.

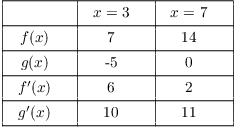
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & & & $x = 3$ & & $x = 7$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $f(x)$ & & 7 & & 14 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $g(x)$ & & -5 & & 0 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $f'(x)$ & & 6 & & 2 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $g'(x)$ & & 10 & & 11 & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Find $(g \circ f)'(3)$ .

By the Chain Rule,

$$(g \circ f)'(3) = g'\left(f(3)\right) \cdot f'(3) = g'(7) \cdot f'(3) = 11 \cdot 6 = 66.\quad\halmos$$

Example. Compute $\displaystyle \der {} x \sin (\sin x)$ .

$$\der {} x \sin (\sin x) = \left[\cos (\sin x)\right] \cdot \cos x.\quad\halmos$$

Example. (a) Compute $\displaystyle \der {} x \left[(\sin x)^2 + \sin (x^2)\right]$ .

(b) Draw a picture to show the difference between the functions $(\sin x)^2$ and $\sin (x^2)$ , considered as composites of $f(x) = \sin x$ and $g(x) = x^2$ .

(a)

$$\der {} x \left[(\sin x)^2 + \sin (x^2)\right] = 2 (\sin x)(\cos x) + 2x\cdot \cos (x^2).\quad\halmos$$

(b) Here's a picture showing the difference between $(\sin x)^2$ and $\sin (x^2)$ :

$$\matrix{ \left(\hphantom{\sin x}\right)^2 & \qquad & \sin \left(\hphantom{x^2}\right) \cr \uparrow & & \hphantom{\sin} \uparrow \cr \sin x & & \hphantom{\sin} x^2 \cr}$$

In the first case, the outer function is the squaring function; in the second case, the outer function is the sine function.

Example. The derivative formulas for $\tan x$ and $\cot x$ are

$$\der {} x \tan x = (\sec x)^2 \quad\hbox{and}\quad \der {} x \cot x = -(\csc x)^2.$$

Taking these for granted, find:

(a) $\displaystyle \der {} x \tan \dfrac{1}{x}$ .

(b) $\displaystyle\der {} x \sqrt{\cot (3x + 1)}$ .

(a)

$$\der {} x \tan \dfrac{1}{x} = \left(\sec \dfrac{1}{x}\right)^2 \cdot \left(-\dfrac{1}{x^2}\right).\quad\halmos$$

(b)

$$\der {} x \sqrt{\cot (3x + 1)} = \dfrac{1}{2} \left(\cot (3x + 1)\right)^{-1/2} \cdot \left[-\cot (3x + 1) \csc (3x + 1)\right]\cdot (3).\quad\halmos$$

Example. Compute $\displaystyle \der {} x \left(1 + \left(1 + x^2\right)^2\right)^2$ .

Differentiate from the outside in:

$$\der {} x \left(1 + \left(1 + x^2\right)^2\right)^2 = 2 \left(1 + \left(1 + x^2\right)^2\right)\cdot 2 \left(1 + x^2\right)\cdot (2x).\quad\halmos$$

Example. Where does the graph of $f(x) = (x^2 - 2x + 7)^{-50}$ have a horizontal tangent?

$$f'(x) = (-50)(x^2 - 2x + 7)^{-51}\cdot (2x - 2) = \dfrac{(-50)(2x - 2)}{(x^2 - 2x + 7)^{51}}.$$

Set $f'(x) = 0$ and solve for x:

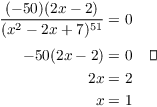
$$\eqalign{ \dfrac{(-50)(2 x - 2)}{(x^2 - 2 x + 7)^{51}} & = 0 \cr \noalign{\vskip2pt} -50 (2 x - 2) & = 0 \cr 2 x & = 2 \cr x & = 1 \cr} \quad\halmos$$

The proof of the Chain Rule.

This section is fairly technical, so you can probably skip it if you're reading this for first-term calculus.

Lemma. If f is differentiable at a, there is a continuous function $p(h)$ which satisfies:

(a) $\displaystyle \lim_{h \to 0} p(h) = 0$ .

(b)

$$f(a + h) - f(a) = (f'(a) + p(h)) \cdot h.$$

Proof. Define

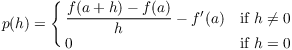
$$p(h) = \cases{ \dfrac{f(a + h) - f(a)}{h} - f'(a) & if $h \ne 0$ \cr \noalign{\vskip2pt} 0 & if $h = 0$ \cr}$$

Then

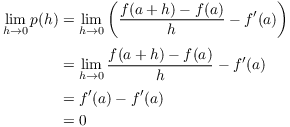
$$\eqalign{ \lim_{h \to 0} p(h) & = \lim_{h \to 0} \left(\dfrac{f(a + h) - f(a)}{h} - f'(a)\right) \cr \noalign{\vskip2pt} & = \lim_{h \to 0}\dfrac{f(a + h) - f(a)}{h} - f'(a) \cr \noalign{\vskip2pt} & = f'(a) - f'(a) \cr & = 0 \cr}$$

Thus,

$$\lim_{h \to 0} p(h) = 0 = p(0).$$

Hence, p is a continuous function. This proves (a).

Note that for $h \ne 0$ ,

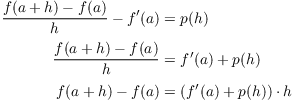
$$\eqalign{ \dfrac{f(a + h) - f(a)}{h} - f'(a) & = p(h) \cr \noalign{\vskip2pt} \dfrac{f(a + h) - f(a)}{h} & = f'(a) + p(h) \cr \noalign{\vskip2pt} f(a + h) - f(a) & = (f'(a) + p(h)) \cdot h \cr}$$

For $h = 0$ , this equation is true, since both sides are 0. This proves (b).

Theorem. ( Chain Rule) Suppose that $f(a)$ . Assume f is differentiable at a and g is differentiable at $f(a)$ . Then the composite $(g \circ f)(x) = g(f(x))$ is differentiable at a, and

$$(g \circ f)(x)'(a) = g'(f(a)) \cdot f'(a).$$

Proof. By the lemma, there are functions p and q such that

$$\lim_{h \to 0} p(h) = 0 \quad\hbox{and}\quad \lim_{k \to 0} q(k) = 0,$$

$$f(a + h) - f(a) = (f'(a) + p(h)) \cdot h,$$

$$g(f(a) + k) - g(f(a)) = (g'(f(a)) + q(k)) \cdot k.$$

Here $k = f(a + h) - f(a)$ . Thus, as $h \to 0$ , I have $k \to 0$ . By the rule for the limit of a composite, this means that as $h \to 0$ , I have $q(k) \to 0$ .

The next few steps may be a little hard to follow, so I'll give some detail before I do the computation.

I will take the equation $g(f(a) + k) - g(f(a)) = (g'(f(a)) + q(k)) \cdot k$ and substitute as follows:

1. On the left side, I'll plug in $k = f(a + h) - f(a)$ .

2. On the right side I'll plug in $k = f(a + h) - f(a) = (f'(a) + p(h)) \cdot h$ in for k.

Now here's the computation:

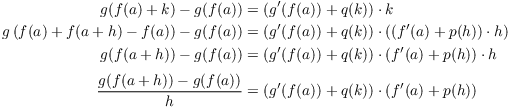
$$\eqalign{ g(f(a) + k) - g(f(a)) & = (g'(f(a)) + q(k)) \cdot k \cr g\left(f(a) + f(a + h) - f(a)\right) - g(f(a)) & = (g'(f(a)) + q(k)) \cdot \left((f'(a) + p(h)) \cdot h\right) \cr g(f(a + h)) - g(f(a)) & = (g'(f(a)) + q(k)) \cdot (f'(a) + p(h)) \cdot h \cr \noalign{\vskip2pt} \dfrac{g(f(a + h)) - g(f(a))}{h} & = (g'(f(a)) + q(k)) \cdot (f'(a) + p(h)) \cr}$$

Now take the limit as $h \to 0$ on both sides. Remember that as $h \to 0$ , I have both $p(h) \to 0$ and $q(k) \to 0$ .

$$(g \circ f)(x)'(a) = \lim_{h \to 0} \dfrac{g(f(a + h)) - g(f(a))}{h} = \lim_{h \to 0} (g'(f(a)) + q(k)) \cdot (f'(a) + p(h)) = g'(f(a)) \cdot f'(a).\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga